Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute Chladni figures
ResourceFunction["ChladniFigure"][x,y,L,m,n] gives Chladni figures. |
Compute a value at a point:
| In[1]:= |
| Out[1]= |
Plot only contours:
| In[2]:= |
| Out[2]= | 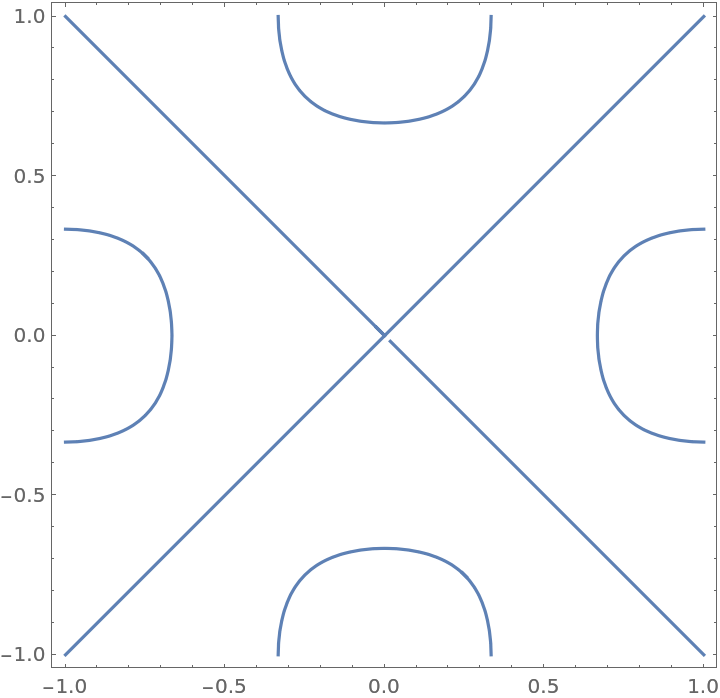 |
With full color:
| In[3]:= | ![ContourPlot[
Evaluate[
ResourceFunction["ChladniFigure"][x, y, 1., 1., 2.]], {x, -1., 1.}, {y, -1., 1.}, ColorFunction -> "Rainbow"]](https://www.wolframcloud.com/obj/resourcesystem/images/4e9/4e9e2b67-095b-4ae7-a2d7-49d40ab954e6/2bc9371e51485719.png) |
| Out[3]= | 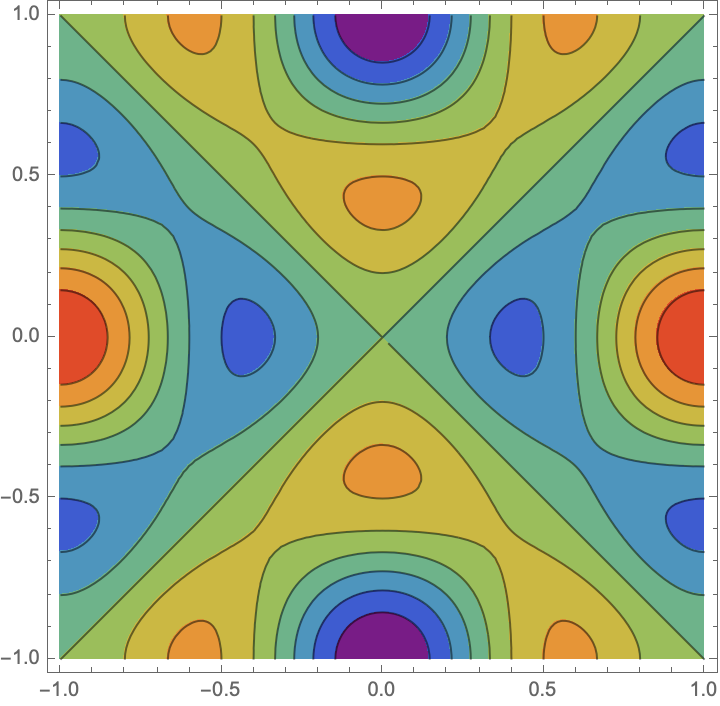 |
Make a 3D plot:
| In[4]:= | ![Plot3D[Evaluate[
ResourceFunction["ChladniFigure"][x, y, 1., 1., 2.]], {x, -1., 1.}, {y, -1., 1.}, ColorFunction -> "Rainbow", MeshFunctions -> {#3 &}]](https://www.wolframcloud.com/obj/resourcesystem/images/4e9/4e9e2b67-095b-4ae7-a2d7-49d40ab954e6/577a66d3b3e13dcf.png) |
| Out[4]= | 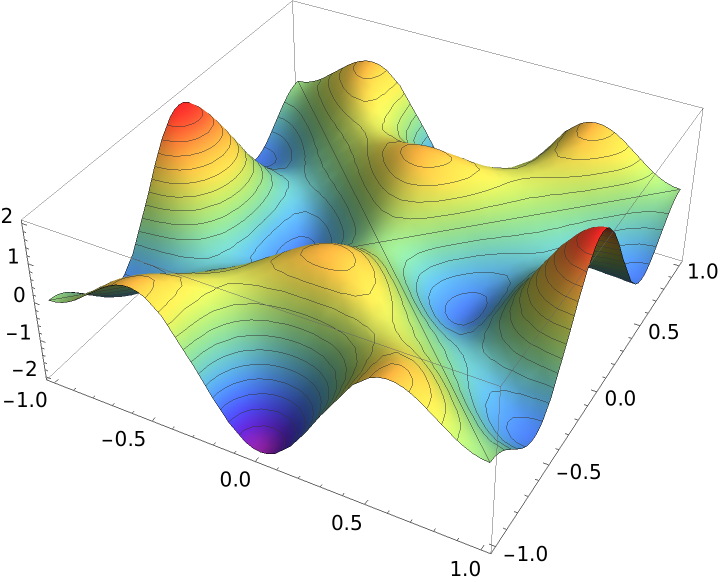 |
Get a higher resolution:
| In[5]:= | ![ContourPlot[
Evaluate[
ResourceFunction["ChladniFigure"][x, y, 1., 2., 3.]], {x, -2., 2.}, {y, -2., 2.}, ColorFunction -> "Rainbow", Contours -> 5, MaxRecursion -> 3]](https://www.wolframcloud.com/obj/resourcesystem/images/4e9/4e9e2b67-095b-4ae7-a2d7-49d40ab954e6/34f547564b1d4d69.png) |
| Out[5]= | 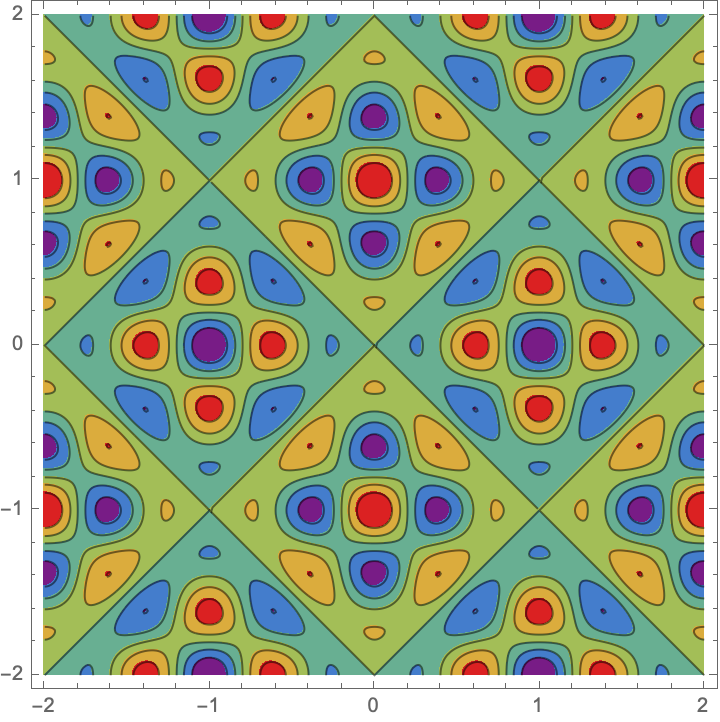 |
For m=n:
| In[6]:= | ![Module[{L = 1., m = 1., n = 1.}, ContourPlot[
Evaluate[ResourceFunction["ChladniFigure"][x, y, L, m, n]], {x, -1.,
1.}, {y, -1., 1.}, ColorFunction -> "Rainbow"]]](https://www.wolframcloud.com/obj/resourcesystem/images/4e9/4e9e2b67-095b-4ae7-a2d7-49d40ab954e6/0410e3105decf412.png) |
| Out[6]= | 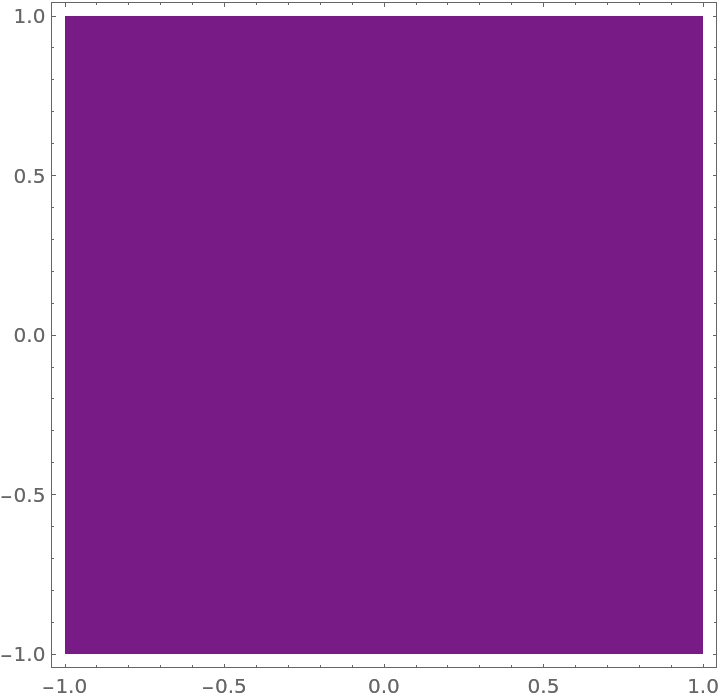 |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License