Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ChirpFunction

Source Notebook

Generate a swept-frequency sinusoidal function

Contributed by: Gustavo Delfino

ResourceFunction["ChirpFunction"][]

generates a function for a chirp signal.

Details and Options

A chirp is also referred to as a swept sinusoid signal.
Chirp functions are typically used as excitation signals for system identification.
The resulting function is given as a CompiledFunction.
ResourceFunction["ChirpFunction"] supports the following options:
“InitialFrequency"1initial frequency in Hz
“FinalFrequency"100final frequency in Hz
"Duration"1final time in seconds
"Magnitude"1height of the sinusoidal peaks
"ChirpType""Logarithmic"indicates how the frequency should change. Accepted values are "Logarithmic" and "Linear"
"Sinusoid"CosSin will give a smooth start. Cos will give an abrupt start.
"AmplitudeRampFraction"0fraction of window length for amplitude ramps. Accepts values from 0 to 0.5.

Examples

Basic Examples (6) 

ChirpFunction returns a compiled function:

In[1]:=
f = ResourceFunction["ChirpFunction"][]
Out[1]=

The default cosine base sinusoid goes from 1 Hz to 100 Hz logarithmically over the a time of one second:

In[2]:=
Plot[f[t], {t, 0, 1}, AspectRatio -> 1/8, ImageSize -> Full]
Out[2]=

Adjust the frequency range for audibility and hear the result:

In[3]:=
f = ResourceFunction["ChirpFunction"]["InitialFrequency" -> 20, "FinalFrequency" -> 4000]; Play[f[t], {t, 0, 1}]
Out[4]=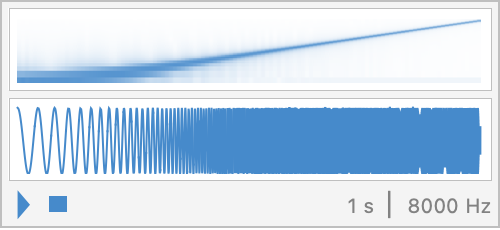

By varying the frequency linearly, the initial lower frequencies are deemphasized:

In[5]:=
f = ResourceFunction["ChirpFunction"]["InitialFrequency" -> 20, "FinalFrequency" -> 4000, "ChirpType" -> "Linear"]; Play[f[t], {t, 0, 1}]
Out[6]=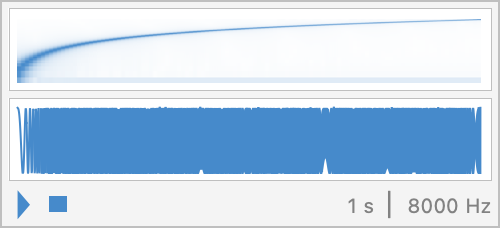

Start the signal at zero:

In[7]:=
f = ResourceFunction[ "ChirpFunction"][{"ChirpType" -> "Linear", "Sinusoid" -> Sin}]; Plot[f[t], {t, 0, 1}, AspectRatio -> 1/8]
Out[8]=

See the effect of amplitude ramps using the option "AmplitudeRampFraction":

In[9]:=
f = ResourceFunction["ChirpFunction"]["ChirpType" -> "Linear", "Sinusoid" -> Sin, "AmplitudeRampFraction" -> 0.25]; Plot[f[t], {t, 0, 1}, AspectRatio -> 1/8]
Out[10]=

Options can be provided as an Association:

In[11]:=
f = ResourceFunction[ "ChirpFunction"][<|"InitialFrequency" -> .1, "FinalFrequency" -> 200, "Magnitude" -> 10, "Duration" -> 1|>]; Plot[f[t], {t, 0, 1}, AspectRatio -> 1/8]
Out[12]=

Use a longer duration:

In[13]:=
f = ResourceFunction[ "ChirpFunction"][<|"InitialFrequency" -> 1, "FinalFrequency" -> 200, "Magnitude" -> 10, "Duration" -> 2|>]; Plot[f[t], {t, 0, 2}, AspectRatio -> 1/8, ImageSize -> Full]
Out[14]=

Scope (5) 

The following examples show the effect of the chirp configuration on the power spectrum:

In[15]:=
chirpParams = <|"InitialFrequency" -> 50, "FinalFrequency" -> 1000, "Duration" -> 0.1|>; sampleTime = .0001; gOpts = {AspectRatio -> 1/8, ImageSize -> Full}; chirpPlot[data_] := Column[{ListLinePlot[data, gOpts, PlotLabel -> "Time Domain", AxesLabel -> {"t(s)", ""}], Periodogram[Last /@ data, SampleRate -> 1/sampleTime, gOpts, PlotLabel -> "Power Spectum", AxesLabel -> {"Hz", "dB"}]}];

Logarithmic chirp:

In[16]:=
f = ResourceFunction["ChirpFunction"][chirpParams]; chirpPlot[ Table[{t, f[t]}, {t, 0, chirpParams["Duration"], sampleTime}]]
Out[17]=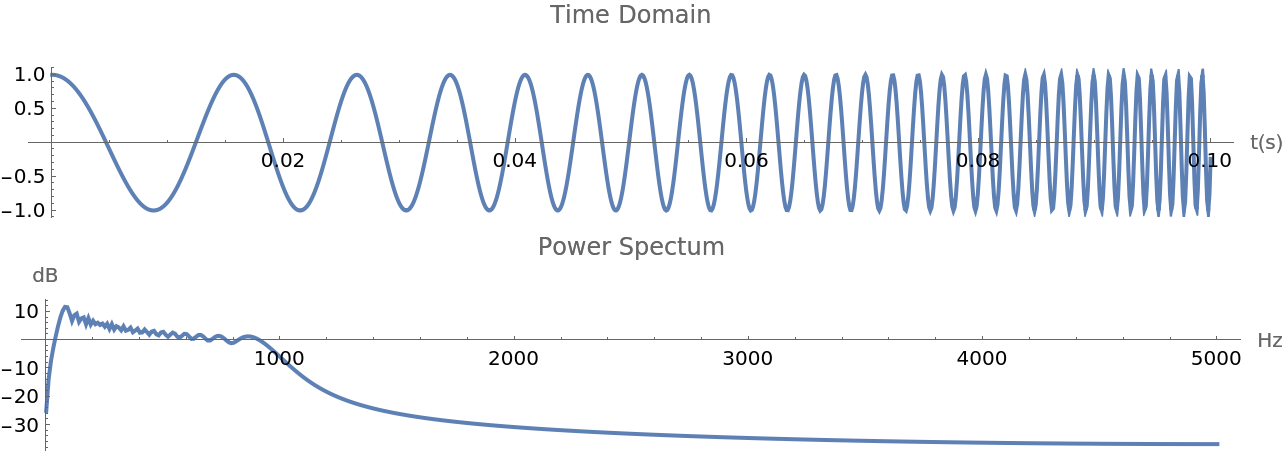

Linear chirp:

In[18]:=
f = ResourceFunction["ChirpFunction"][ Append[chirpParams, "ChirpType" -> "Linear"]]; chirpPlot[ Table[{t, f[t]}, {t, 0, chirpParams["Duration"], sampleTime}]]
Out[19]=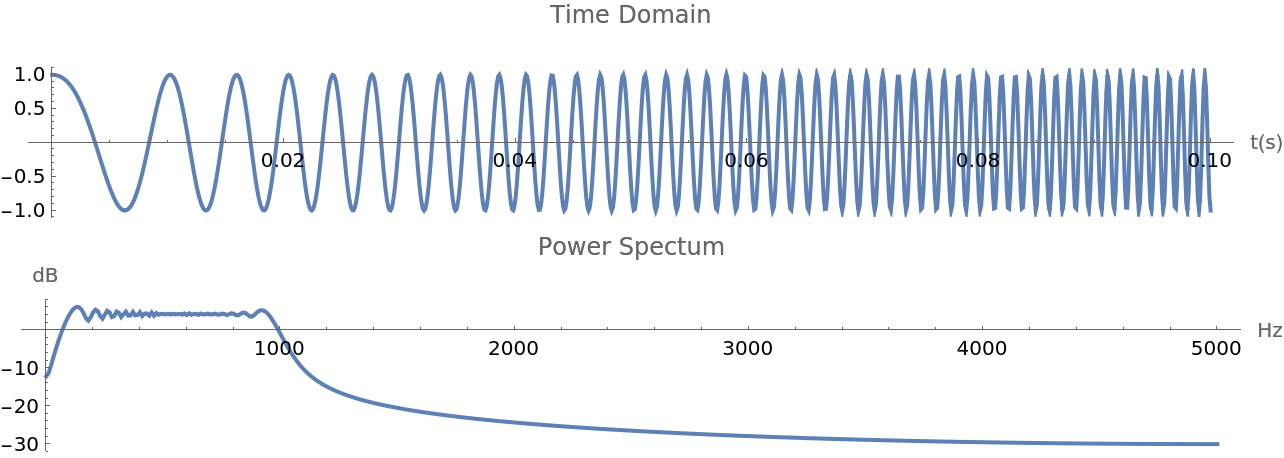

Amplitude adjusted linear chirp:

In[20]:=
f = ResourceFunction["ChirpFunction"][ Append[chirpParams, {"ChirpType" -> "Linear", "AmplitudeRampFraction" -> .1}]]; chirpPlot[ Table[{t, f[t]}, {t, 0, chirpParams["Duration"], sampleTime}]]
Out[21]=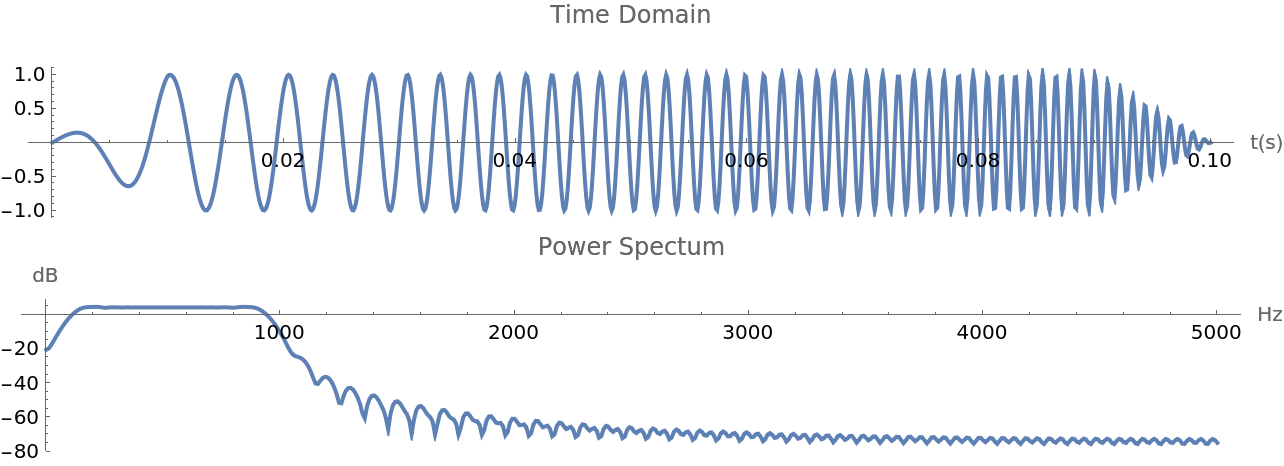

Amplitude adjusted logarithmic chirp:

In[22]:=
f = ResourceFunction["ChirpFunction"][ Append[chirpParams, {"ChirpType" -> "Logarithmic", "AmplitudeRampFraction" -> .1}]]; chirpPlot[ Table[{t, f[t]}, {t, 0, chirpParams["Duration"], sampleTime}]]
Out[23]=

Options (7) 

InitialFrequency (1) 

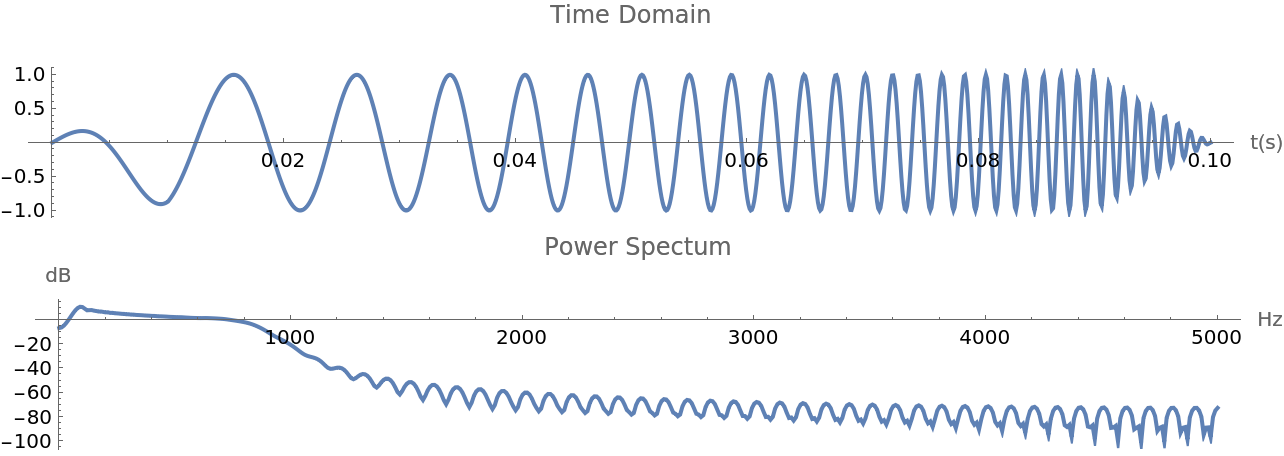Change the initial frequency:

In[24]:=
Column[Map[ With[{f = ResourceFunction["ChirpFunction"][{"InitialFrequency" -> #}]}, Plot[f[t], {t, 0, 1}, AspectRatio -> 1/8, ImageSize -> Full, PlotLabel -> StringTemplate["\"InitialFrequency\" \[Rule] ``"][#]]] &, {.1, 1, 10}]]
Out[24]=

FinalFrequency (1) 

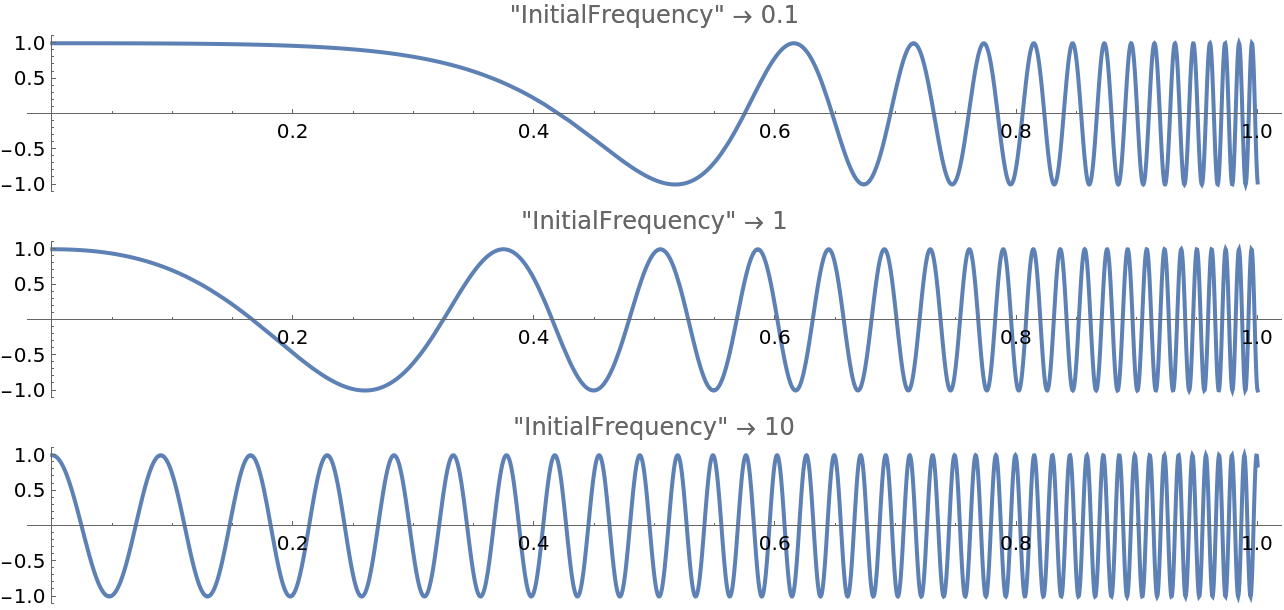Change the final frequency:

In[25]:=
Column[Map[ With[{f = ResourceFunction["ChirpFunction"][{"FinalFrequency" -> #}]}, Plot[f[t], {t, 0, 1}, AspectRatio -> 1/8, ImageSize -> Full, PlotLabel -> StringTemplate["\"FinalFrequency\" \[Rule] ``"][#]]] &, {10, 100, 1000}]]
Out[25]=

Duration (1) 

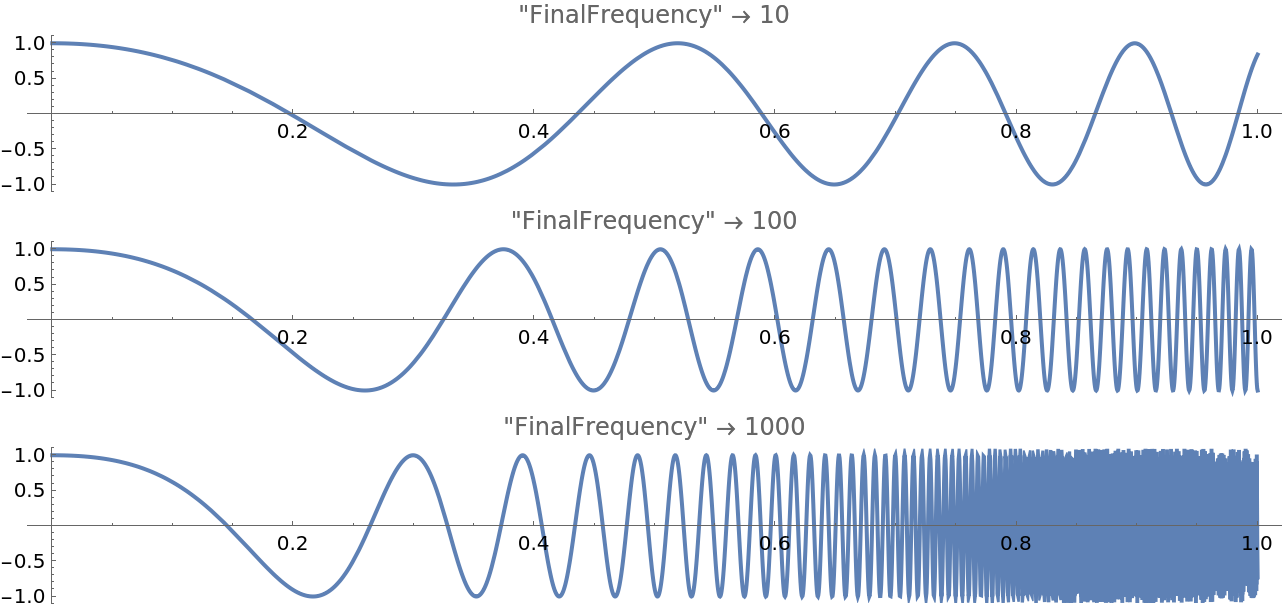Change how long it takes to go from the initial to the final frequency:

In[26]:=
Column[Map[ With[{f = ResourceFunction["ChirpFunction"][{"Duration" -> #}]}, Plot[f[t], {t, 0, #}, AspectRatio -> 1/8, ImageSize -> Full, PlotLabel -> StringTemplate["\"Duration\" \[Rule] ``"][#]]] &, {.5, 1, 2}]]
Out[26]=

Magnitude (1) 

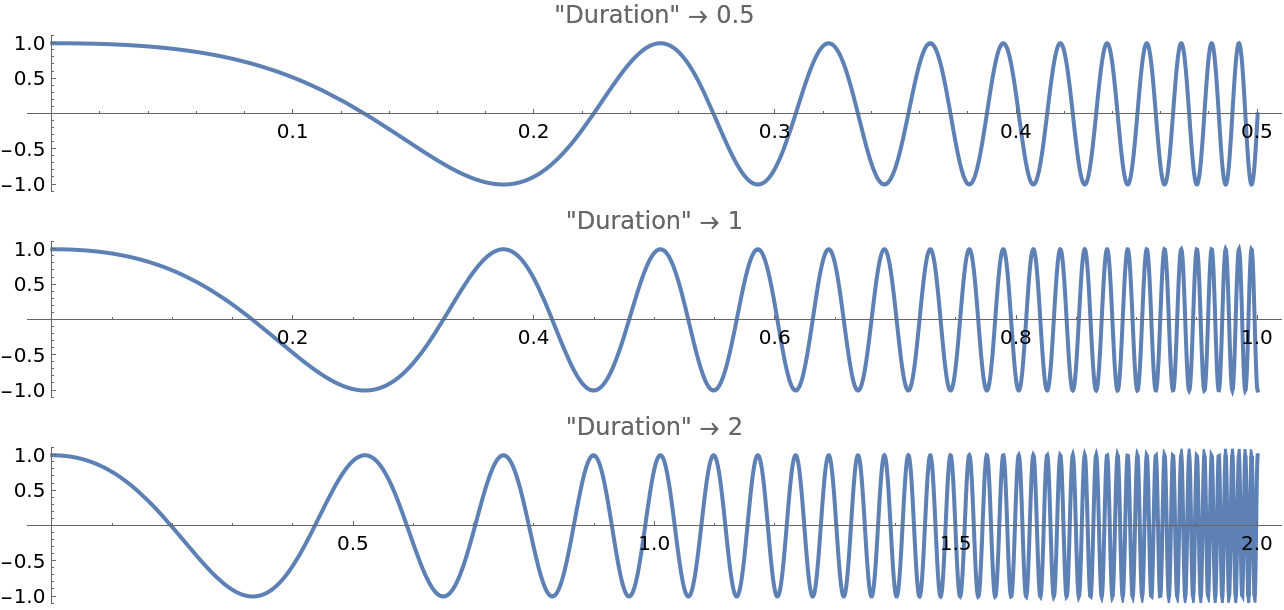Change the magnitude (peak values):

In[27]:=
Column[Map[ With[{f = ResourceFunction["ChirpFunction"][{"Magnitude" -> #}]}, Plot[f[t], {t, 0, 1}, AspectRatio -> 1/8, ImageSize -> Full, PlotRange -> {-3, 3}, PlotLabel -> StringTemplate["\"Magnitude\" \[Rule] ``"][#]]] &, {.25, 1, 3}]]
Out[27]=

ChirpType (1) 

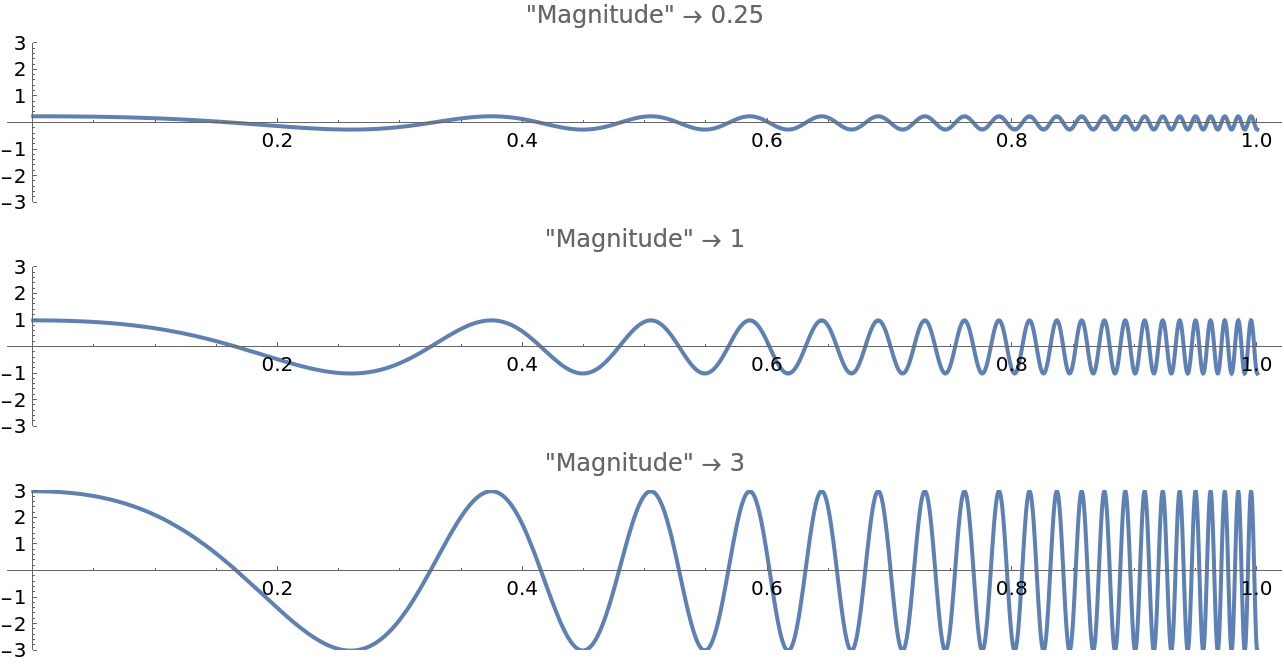Change the function type used to vary the frequency:

In[28]:=
Column[Map[ With[{f = ResourceFunction["ChirpFunction"][{"ChirpType" -> #}]}, Plot[f[t], {t, 0, 1}, AspectRatio -> 1/8, ImageSize -> Full, PlotLabel -> StringTemplate[ "\"ChirpType\" \[Rule] ``"][#]]] &, {"Logarithmic", "Linear"}]]
Out[28]=

Sinusoid (1) 

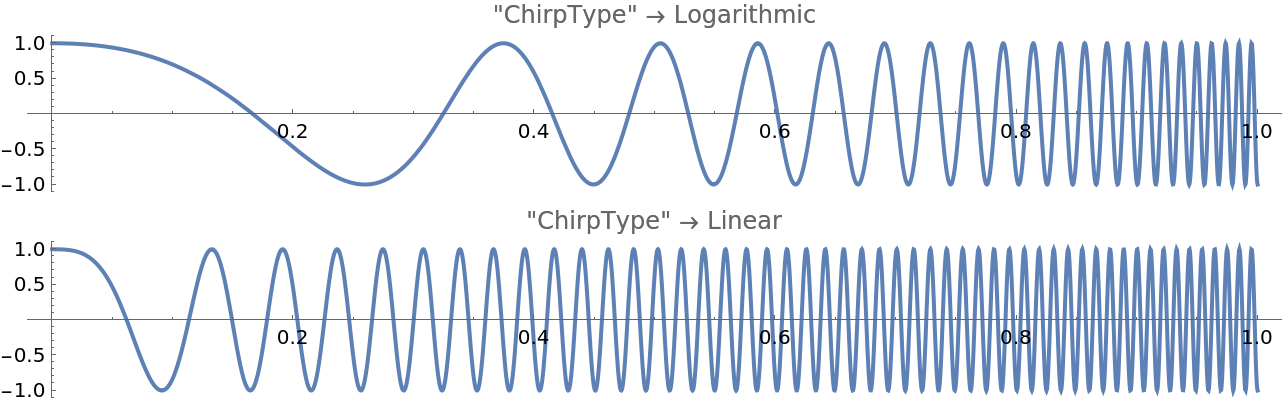A Sin sinusoid results in a smooth rise whereas Cos starts high resembling a step:

In[29]:=
Column[Map[ With[{f = ResourceFunction["ChirpFunction"][{"Sinusoid" -> #}]}, Plot[f[t], {t, 0, 1}, AspectRatio -> 1/8, ImageSize -> Full, PlotLabel -> StringTemplate["\"Sinusoid\" \[Rule] ``"][#]]] &, {Sin, Cos}]]
Out[29]=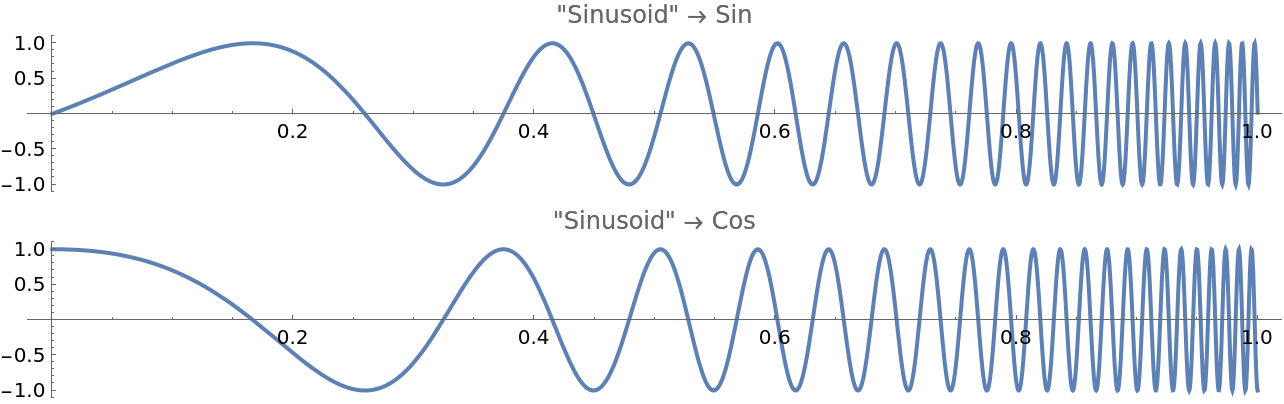

AmplitudeRampFraction (1) 

Amplitude ramps can help reduce transient response effects at the start and end:

In[30]:=
Column[Table[ With[{f = ResourceFunction["ChirpFunction"][ "AmplitudeRampFraction" -> \[Rho], "InitialFrequency" -> 20]}, Plot[f[t], {t, 0, 1}, AspectRatio -> 1/8, ImageSize -> Full, PlotLabel -> StringTemplate["\"\[Rho]\" \[Rule] ``"][\[Rho]]]], {\[Rho], 0, .5, .1}]]
Out[30]=

Possible Issues (1) 

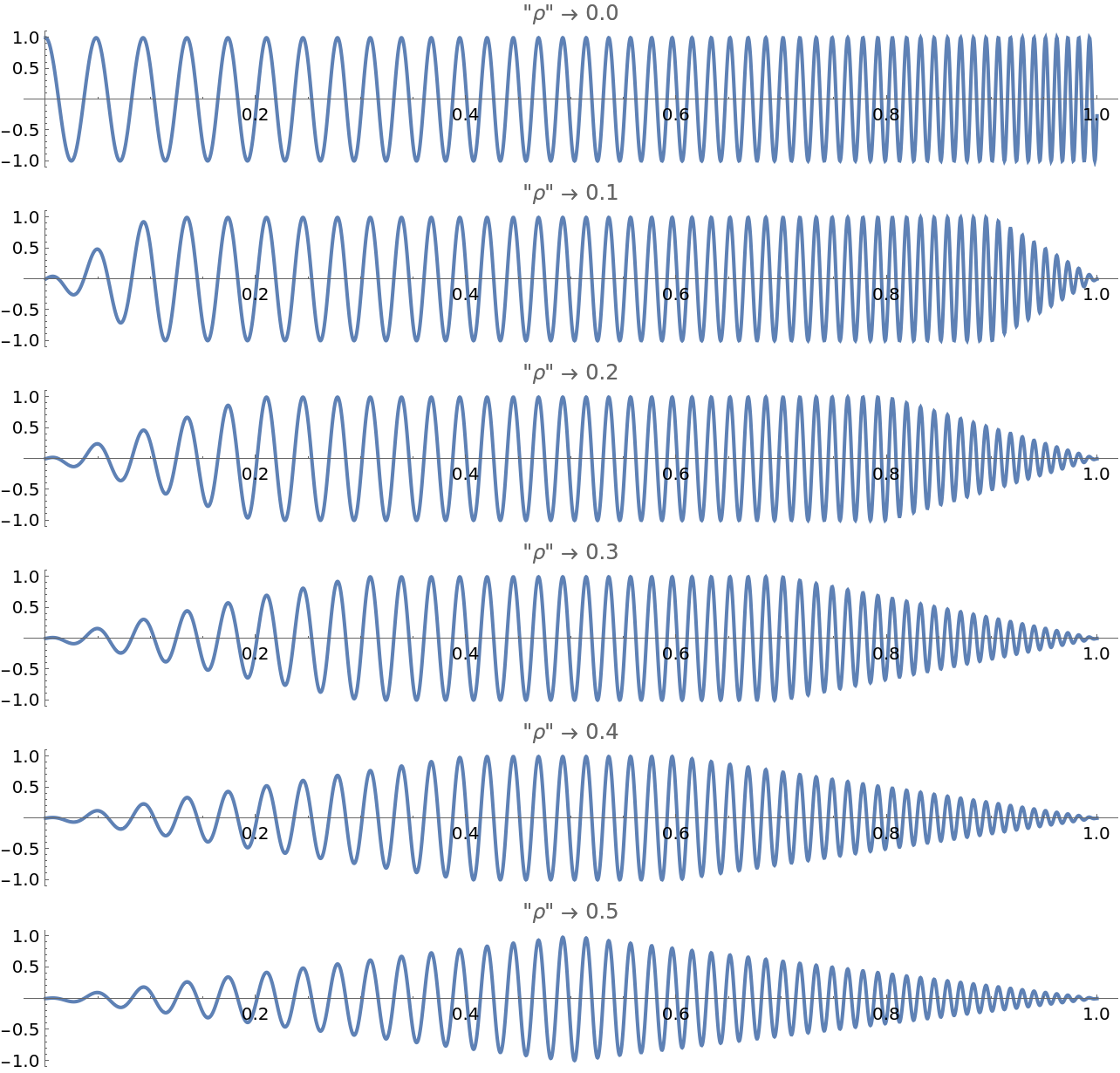The resulting function is not intended to be evaluated for times greater than the specified duration. Doing so will produce unexpected results without warning:

In[31]:=
f = ResourceFunction[ "ChirpFunction"][<|"InitialFrequency" -> 1, "FinalFrequency" -> 100, "Magnitude" -> 10, "Duration" -> 1, "AmplitudeRampFraction" -> .1|>]; Plot[f[t], {t, 0, 1.2}, AspectRatio -> 1/8, ImageSize -> Full]
Out[32]=

Neat Examples (1) 

Create an interactive chirp:

In[33]:=
Manipulate[ With[{excitation = ResourceFunction["ChirpFunction"]["InitialFrequency" -> f0, "FinalFrequency" -> f1, "Duration" -> tmax, "ChirpType" -> type, "Sinusoid" -> f, "AmplitudeRampFraction" -> \[Rho]]}, Plot[excitation[t], {t, 0, tmax}, AspectRatio -> 1/GoldenRatio/4, ImageSize -> Full, PlotPoints -> 300]], {type, {"Linear", "Logarithmic"}}, {{f, Sin, "Sinusoid Function"}, {Sin, Cos}}, {tmax, {0.1, 0.5, 1.0, 2.0, 10}}, {{f0, 100, "Initial f(Hz)"}, 1, 100, 1}, {{f1, 1000, "Final f(Hz)"}, 100, 5000, 100}, {{\[Rho], 0, "Ramp up fraction"}, 0, .5}]
Out[33]=

Publisher

GustavoDelfino

Requirements

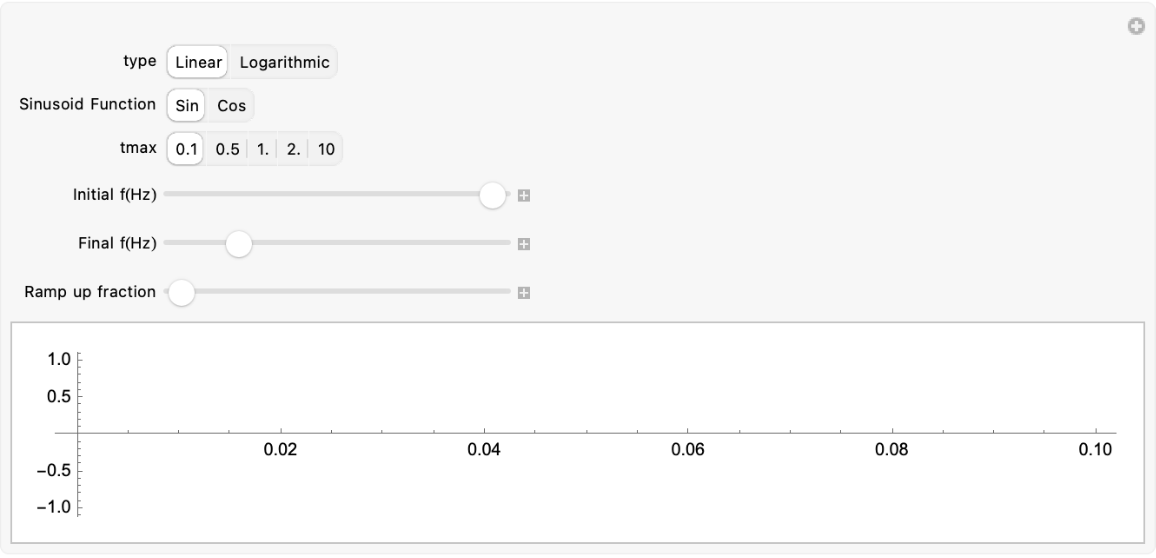Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 11 October 2023

Source Metadata

  • Citation:
    • "Digital Control of Dynamic Systems" by Gene F. Franklin, J. David Powell, Michael L. Workman. Second Edition, page 687.
    • "Mastering System Identification in 100 Exercises" by Johan Schoukens, Rik Pintelon and Yves Rolain. Section 2.3.3: The swept sine signal

License Information