Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Test a sequence of zeroes and ones (or a set of random reals between 0 and 1) for equidistribution and return a p-value
ResourceFunction["ChiSquareRandomnessTest"][sequence] tests a sequence of 0s and 1s, or random reals between 0 and 1, and returns a p-value. | |
ResourceFunction["ChiSquareRandomnessTest"][sequence,"property"] tests a sequence and returns a a property of the test. |
| "TestStatistic" | returns the chi square test statistic |
| "PValue" | returns the p-value associated with the test |
Generate a sequence of random integers and test it for equidistribution:
| In[1]:= |
Visualize the sequence:
| In[2]:= |
| Out[2]= |  |
Apply a chi square randomness test:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
Generate a sequence of random reals and test it for equidistribution:
| In[5]:= |
Visualize the sequence:
| In[6]:= |
| Out[6]= |  |
Apply a chi square randomness test:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
Generate variates of the normal distribution and test if they are equidistributed:
| In[9]:= |
Visualize the variates:
| In[10]:= |
| Out[10]= |  |
| In[11]:= |
| Out[11]= | 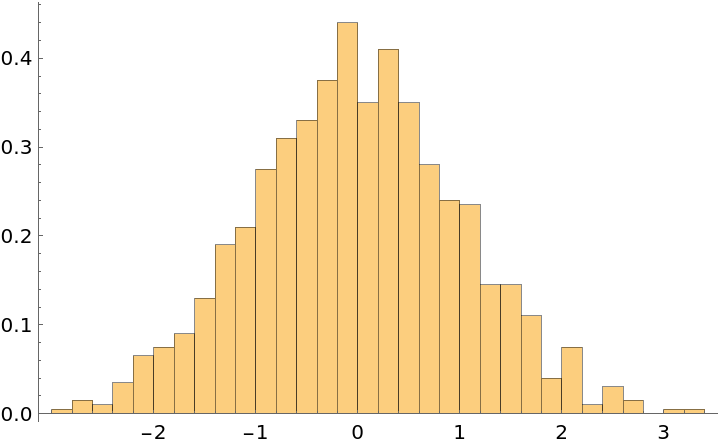 |
Transform the variates so that the range is between 0 and 1:
| In[12]:= |
Visualize the transformed variates:
| In[13]:= |
| Out[13]= |  |
| In[14]:= |
| Out[14]= | 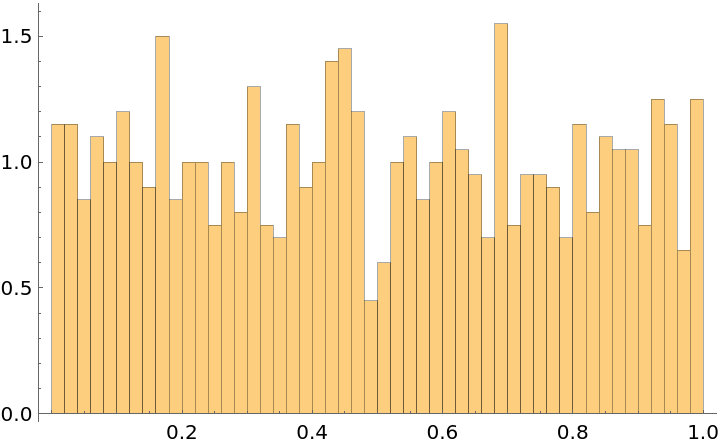 |
Test if the transformed variates are equidistributed:
| In[15]:= |
| Out[15]= |
| In[16]:= |
| Out[16]= |
Test to see if rule 30 is equidistributed:
| In[17]:= |
| In[18]:= |
| Out[18]= |  |
| In[19]:= |
| Out[19]= |
This work is licensed under a Creative Commons Attribution 4.0 International License