Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a chessboard graph where vertices are squares and edges represent legal moves of a chosen piece
ResourceFunction["ChessTourGraph"][piece,n] generates an undirected graph with n2 vertices corresponding to an n×n chessboard, with edges indicating all legal piece moves. | |
ResourceFunction["ChessTourGraph"][piece,{n,m}] generates a graph corresponding to an n×m chessboard. | |
ResourceFunction["ChessTourGraph"]["Bishop",dims,color] generates a graph corresponding to a chessboard of dimension dims, with moves restricted to color squares. |
Generate the king graph in an 8×8 board:
| In[1]:= |
| Out[1]= |  |
Generate the first few square king graphs:
| In[2]:= |
| Out[2]= | 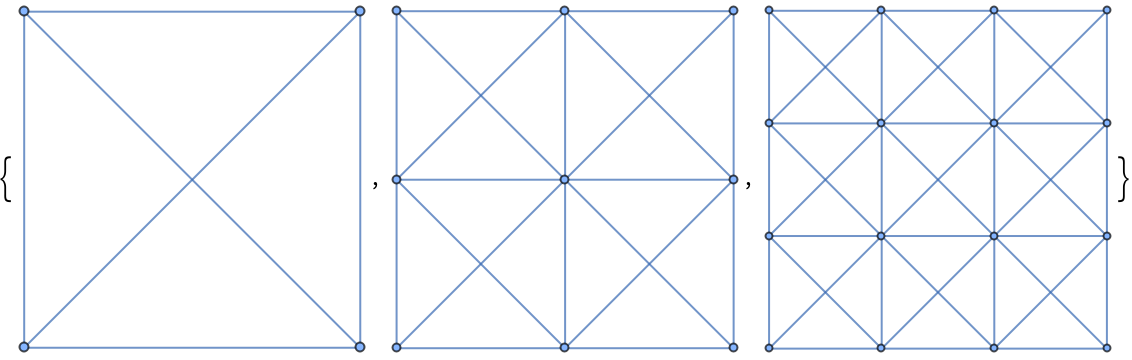 |
Generate some rectangular king graphs:
| In[3]:= |
| Out[3]= | 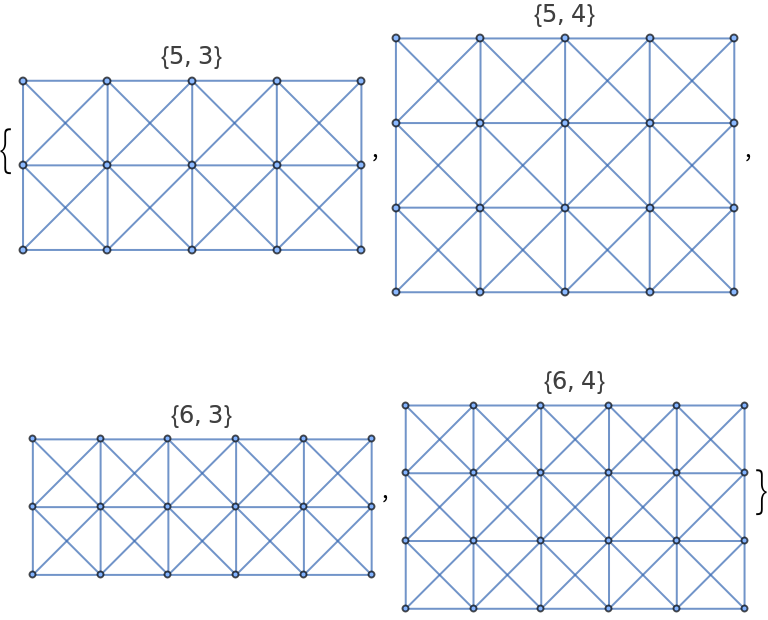 |
Generate the queen graph in an 8×8 board:
| In[4]:= |
| Out[4]= |  |
Generate the first square queen graphs:
| In[5]:= |
| Out[5]= | 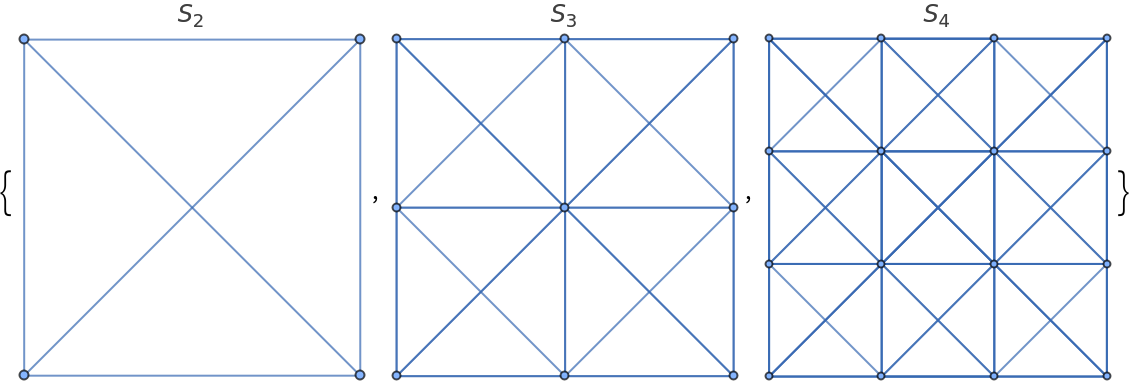 |
Generate some rectangular queen graphs:
| In[6]:= |
| Out[6]= | 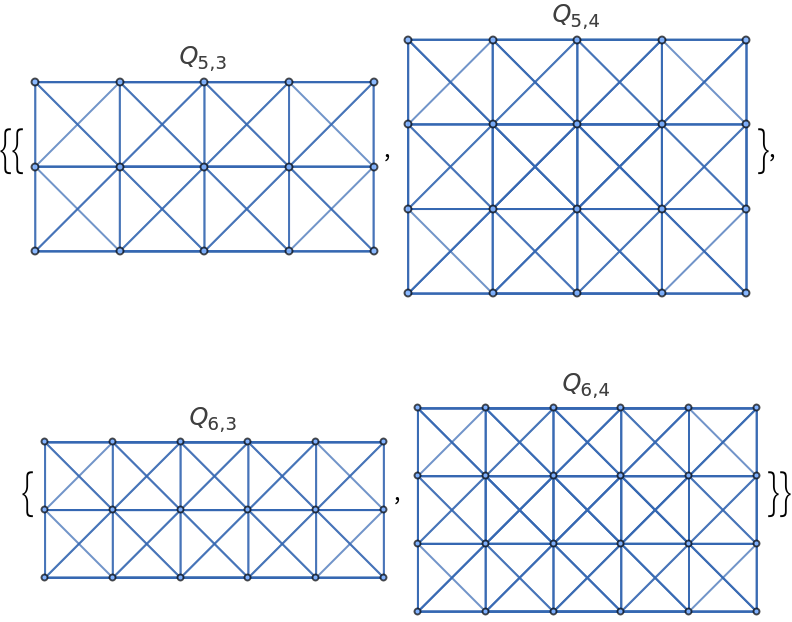 |
Generate the rook graph in an 8×8 board:
| In[7]:= |
| Out[7]= |  |
Generate the first few square rook graphs:
| In[8]:= |
| Out[8]= |  |
Generate some rectangular rook graphs:
| In[9]:= |
| Out[9]= | 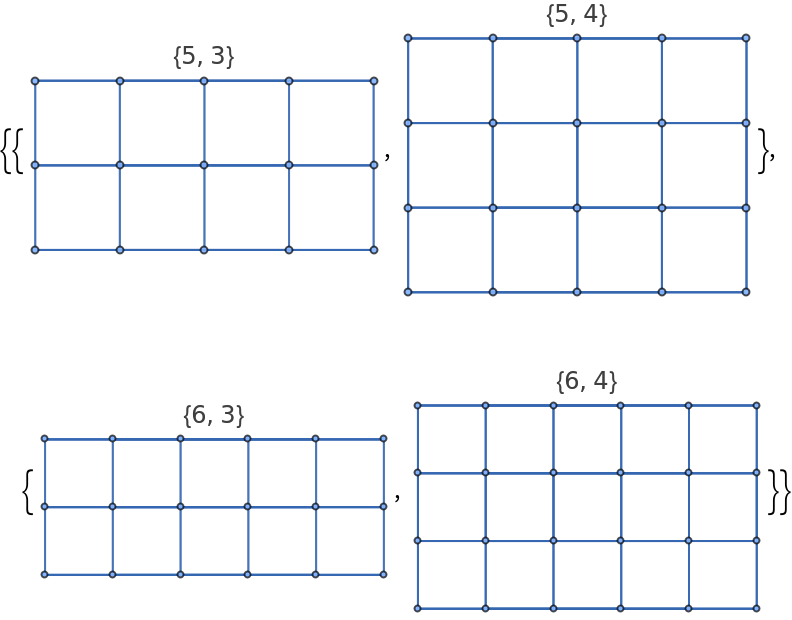 |
Generate the knight graph in an 8×8 board:
| In[10]:= |
| Out[10]= |  |
Generate the first few square knight graphs:
| In[11]:= |
| Out[11]= |  |
Generate some rectangular rook graphs:
| In[12]:= |
| Out[12]= | 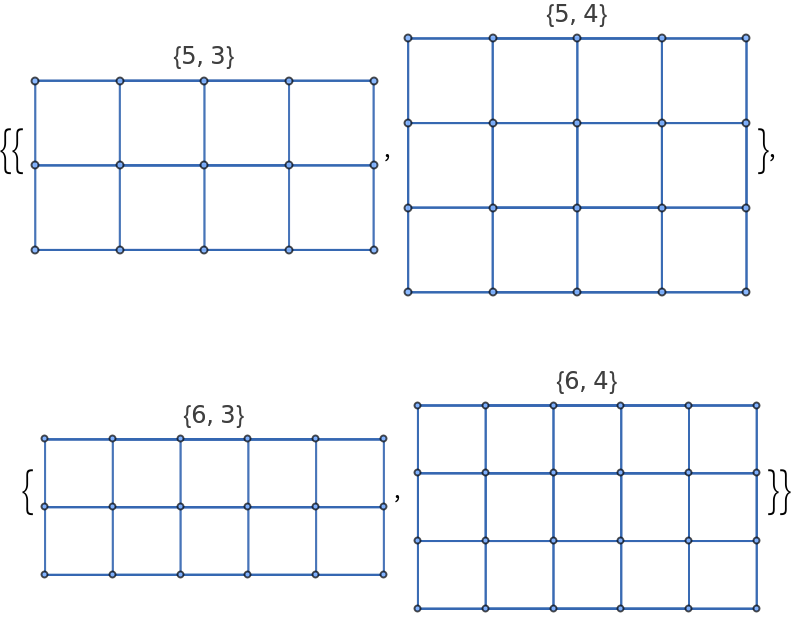 |
Generate a standard 8×8 bishop graph:
| In[13]:= |
| Out[13]= | 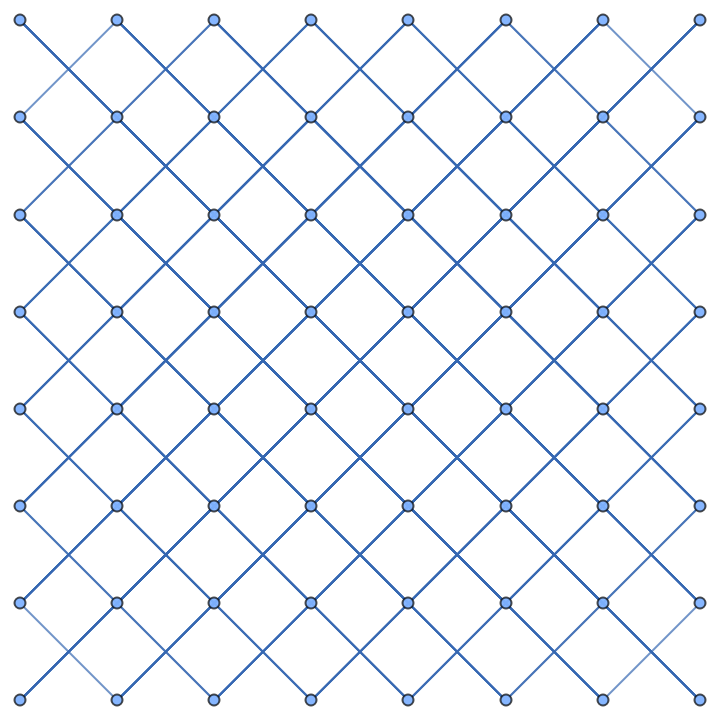 |
Generate a rectangular bishop graph for a 5×3 board:
| In[14]:= |
| Out[14]= | 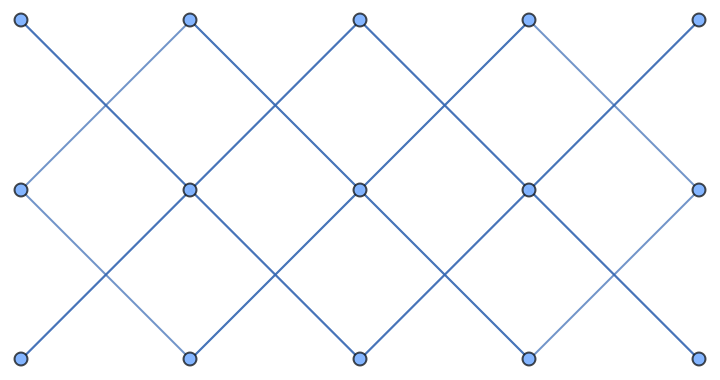 |
Show the white bishop movement on any size board:
| In[15]:= |
| Out[15]= |  |
Show the black bishop movement on any size board:
| In[16]:= |
| Out[16]= |  |
Generate the first few square bishop graphs:
| In[17]:= |
| Out[17]= | 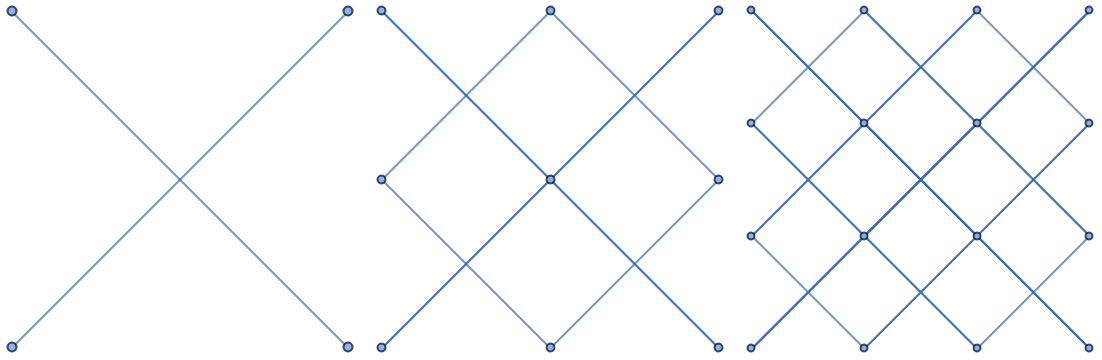 |
Generate some rectangular bishop graphs:
| In[18]:= |
| Out[18]= | 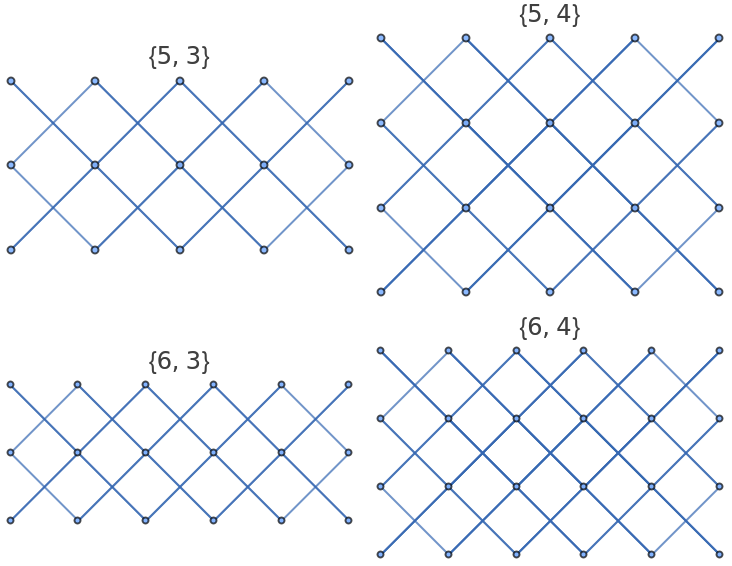 |
The graph is automatically laid out in the order of the appearance of the square numbering on the chessboard:
| In[19]:= |
| Out[19]= | 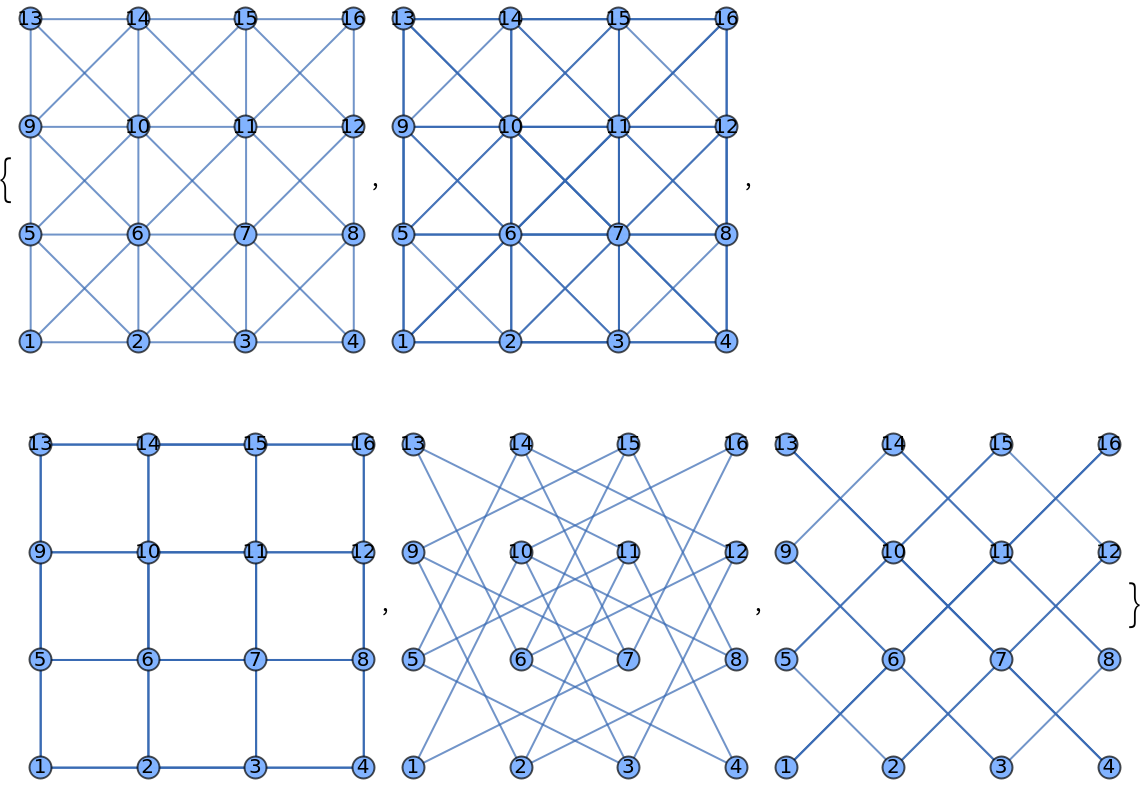 |
Highlight vertex 1:
| In[20]:= | ![HighlightGraph[
ResourceFunction[
"ChessTourGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"]["Bishop", 6, VertexSize -> Medium], {1}, VertexLabels -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/a08/a08d3453-9e8c-442e-897d-d750c09fc007/327fb0870954593e.png) |
| Out[20]= | 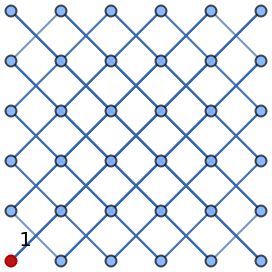 |
Highlight the edge 26:
| In[21]:= | ![HighlightGraph[
ResourceFunction[
"ChessTourGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"]["Queen", 5, VertexSize -> Medium], 2 \[UndirectedEdge] 6, EdgeLabels -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/a08/a08d3453-9e8c-442e-897d-d750c09fc007/63a3ca5c3f5035c5.png) |
| Out[21]= | 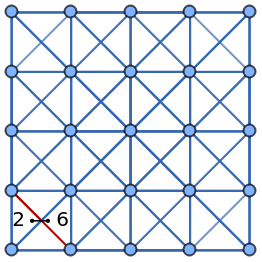 |
Label individual vertices:
| In[22]:= |
| Out[22]= | 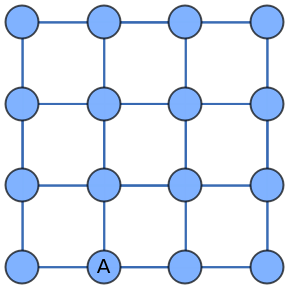 |
Label all vertices:
| In[23]:= |
| Out[23]= | 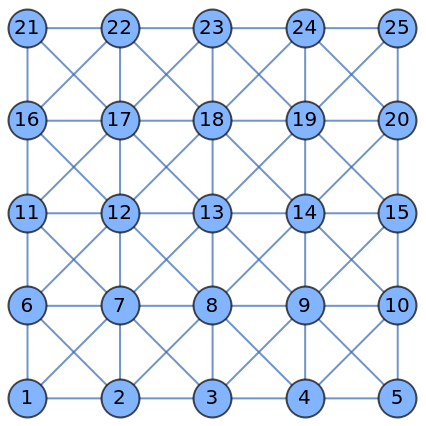 |
By default, the size of vertices is computed automatically:
| In[24]:= |
| Out[24]= |  |
Specify the size of all vertices using symbolic vertex size:
| In[25]:= | ![Table[ResourceFunction[
"ChessTourGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"]["Queen", 4, VertexSize -> s, PlotLabel -> s], {s, {Tiny, Small, Medium, Large}}]](https://www.wolframcloud.com/obj/resourcesystem/images/a08/a08d3453-9e8c-442e-897d-d750c09fc007/5175818a0ea773ab.png) |
| Out[25]= | 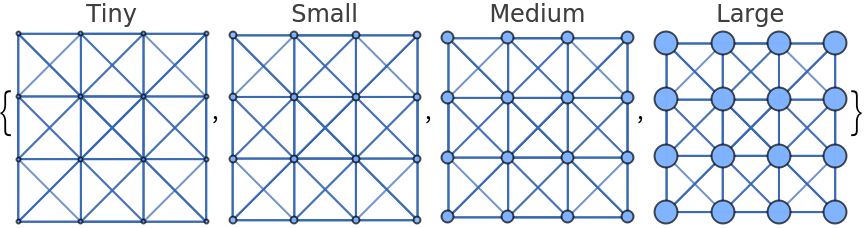 |
Use curved edges to show all the edges:
| In[26]:= |
| Out[26]= |  |
Visualize valid moves for a given piece located at a given position:
| In[27]:= | ![HighlightGraph[
ResourceFunction[
"ChessTourGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][#, {12, 10}], NeighborhoodGraph[
ResourceFunction[
"ChessTourGraph", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][#, {12, 10}], 53], VertexStyle -> {53 -> Blue}, VertexSize -> {53 -> Medium}, VertexSize -> Medium] & /@ {"King", "Queen", "Rook", "Knight", "Bishop"}](https://www.wolframcloud.com/obj/resourcesystem/images/a08/a08d3453-9e8c-442e-897d-d750c09fc007/5c434367e24d763c.png) |
| Out[27]= |  |
The vertex coloring of the queen graph:
| In[28]:= |
| In[29]:= |
| Out[29]= | 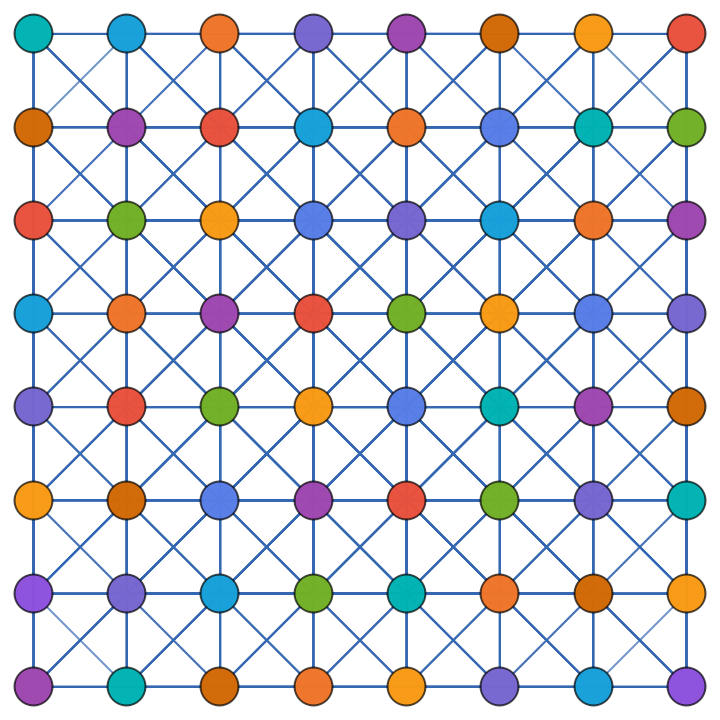 |
The king graph can also be constructed as the strong product of two path graphs. The strong product of any two graphs can be constructed as the union of two other products of the same two graphs, the Cartesian product of graphs and the tensor product of graphs:
| In[30]:= | ![CartesianProductG = GraphProduct[PathGraph[Range[4]], PathGraph[Range[4]], "Cartesian"];
TensorProductG = GraphProduct[PathGraph[Range[4]], PathGraph[Range[4]], "Tensor"];
StrongProductG = GraphUnion[CartesianProductG, TensorProductG];](https://www.wolframcloud.com/obj/resourcesystem/images/a08/a08d3453-9e8c-442e-897d-d750c09fc007/57782fc6650ef73c.png) |
| In[31]:= |
| Out[31]= |
In some board cases, the king graph can also be constructed using GraphData:
| In[32]:= |
| Out[32]= |  |
However, not all board sizes are supported by GraphData:
| In[33]:= |
| Out[33]= |
Rook graphs are the Cartesian product of two complete graphs:
| In[34]:= |
| In[35]:= |
| Out[35]= |
Rook graphs are the line graphs of complete bipartite graphs:
| In[36]:= |
| In[37]:= |
| Out[37]= |
Rook graphs are highly symmetric: for square boards, they are vertex-transitive, edge-transitive, and distance-transitive:
| In[38]:= |
| Out[38]= |
| In[39]:= |
| Out[39]= |
In some board cases, a rook graph can also be constructed using GraphData:
| In[40]:= |
| Out[40]= |  |
However, not all board sizes are supported by GraphData:
| In[41]:= |
| Out[41]= |
Observe the connected components of the bishop graph on a 3×3 board that correspond to the white and black bishop:
| In[42]:= |
| Out[42]= | 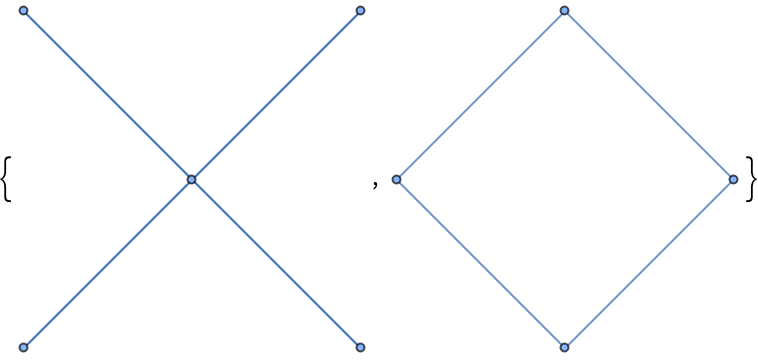 |
All bishop graphs are perfect:
| In[43]:= |
| Out[43]= |
| In[44]:= |
| Out[44]= |
S. Wagon showed that the white bishop graph B(m,n) is Hamiltonian for 4≤m≤n and when m=3 and n≥4:
| In[45]:= |
| Out[45]= |
| In[46]:= |
| Out[46]= |
| In[47]:= |
| Out[47]= |
And nonhamiltonian for m=n=3 and the trivial cases or 1:
| In[48]:= |
| Out[48]= |
| In[49]:= |
| Out[49]= |
In some board cases, the bishop graph can also be constructed using GraphData:
| In[50]:= |
| Out[50]= | 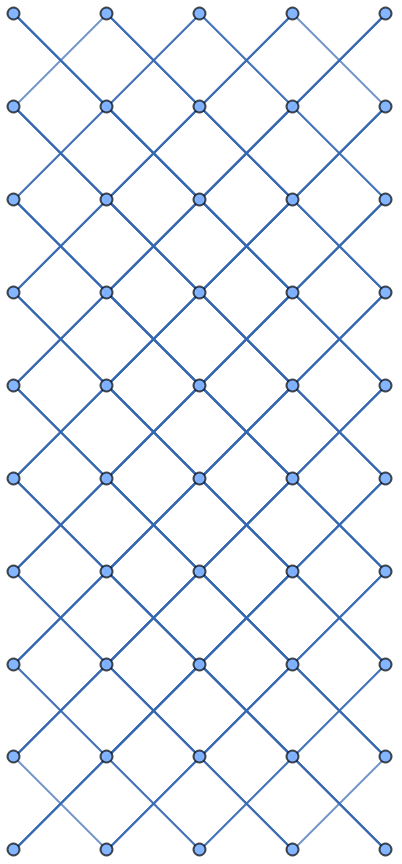 |
However, not all board sizes are supported by GraphData:
| In[51]:= |
| Out[51]= |
The setting DirectedEdges→True will not work:
| In[52]:= |
| Out[52]= | 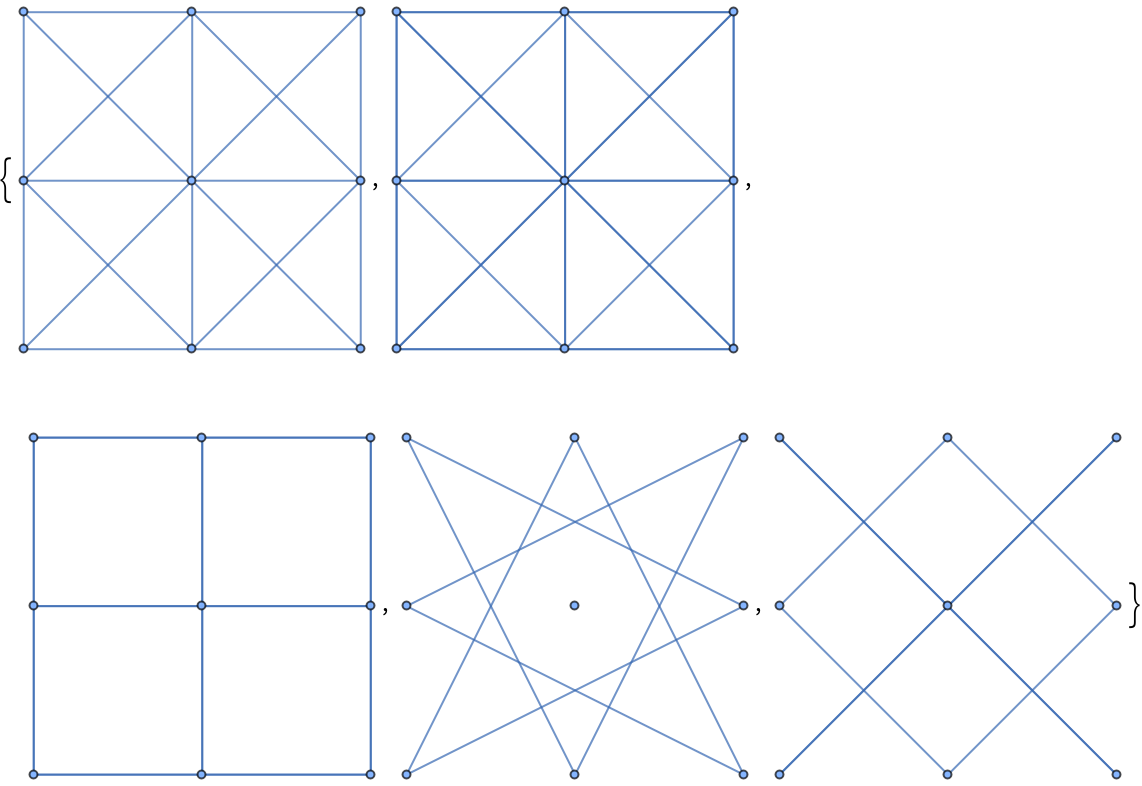 |
ChessTourGraph can produce empty or null graphs when 0 or 1 is specified as the size:
| In[53]:= |
| Out[53]= |  |
Visualize the vertex coloring of the king graph:
| In[54]:= |
| In[55]:= |
| Out[55]= | 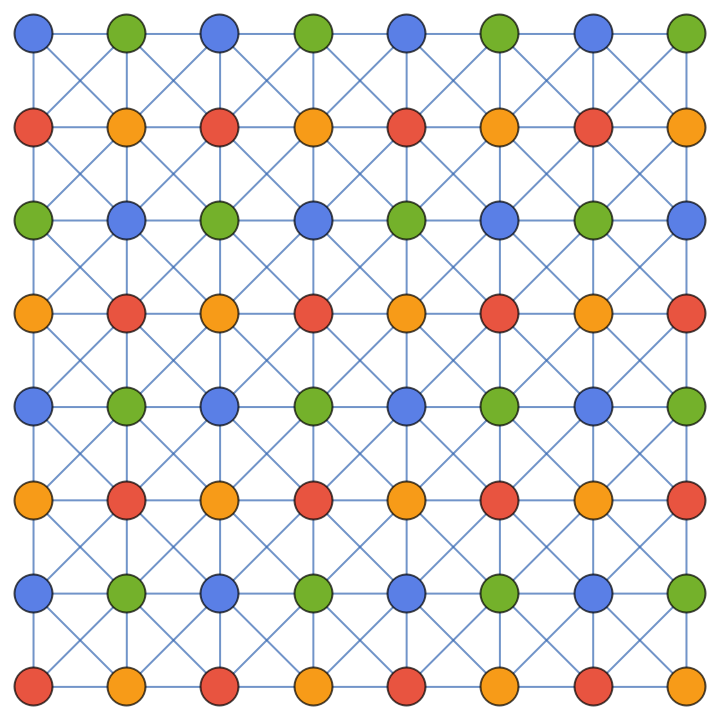 |
Visualize the bishop graph with vertices shown as colored squares matching their color on the chessboard:
| In[56]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/1af66396-1bfd-4ee2-8706-5b25e119332d"]](https://www.wolframcloud.com/obj/resourcesystem/images/a08/a08d3453-9e8c-442e-897d-d750c09fc007/793058b4abcd12d7.png) |
| Out[56]= |  |
Find the shortest path for a knight to cross the board:
| In[57]:= |
| In[58]:= |
| Out[58]= |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License