Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Calculate the value of the first Chebyshev function θ(x)
ResourceFunction["ChebyshevTheta"][x] returns the value of the first Chebyshev function at x. |
Compute θ(30):
| In[1]:= |
| Out[1]= |
Obtain a decimal approximation:
| In[2]:= |
| Out[2]= |
Plot θ(x) from 0 to 30:
| In[3]:= |
| Out[3]= | 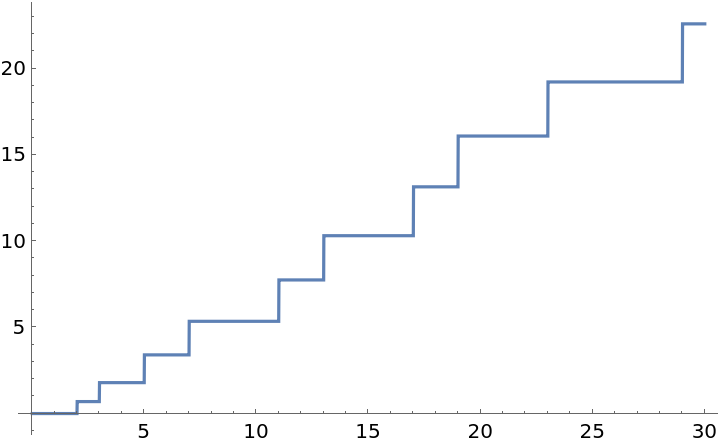 |
Compare x, θ(x) and |x-θ(x)|:
| In[4]:= | ![Plot[{x, ResourceFunction["ChebyshevTheta"][x], Abs[x - ResourceFunction["ChebyshevTheta"][x]]}, {x, 0, 30}, PlotLegends -> {"\!\(\*
StyleBox[\"x\", \"TI\"]\)", "\[Theta](\!\(\*
StyleBox[\"x\", \"TI\"]\))", "|\!\(\*
StyleBox[\"x\", \"TI\"]\)-\[Theta](\!\(\*
StyleBox[\"x\", \"TI\"]\))|"}]](https://www.wolframcloud.com/obj/resourcesystem/images/ee5/ee5f5472-308d-448f-98ab-b059536c5c3d/73e2937f0a091246.png) |
| Out[4]= | 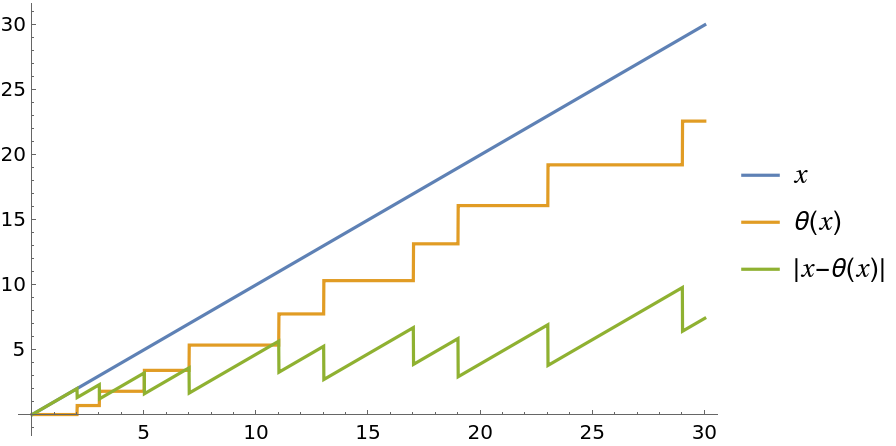 |
Plot the ratio ![]() :
:
| In[5]:= |
| Out[5]= | 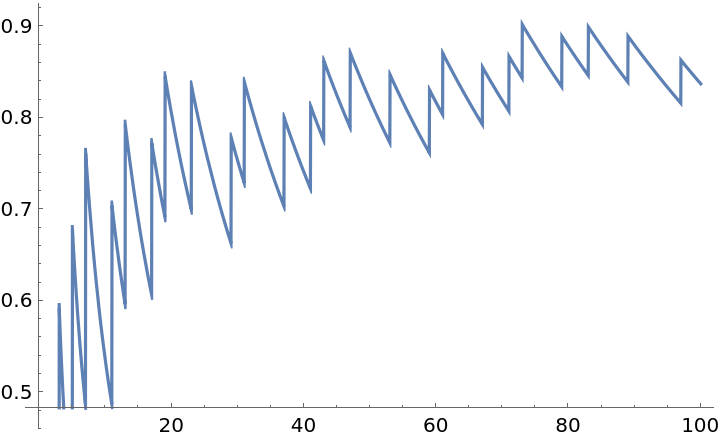 |
This work is licensed under a Creative Commons Attribution 4.0 International License