Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get a numerically sorted list of abscissas for Chebyshev equal-weight quadrature
ResourceFunction["ChebyshevQuadratureAbscissas"][n,{a,b}] gives a list of the n abscissas xi of the n-point Chebyshev equal-weight formula for quadrature on the interval a to b. | |
ResourceFunction["ChebyshevQuadratureAbscissas"][n,{a,b},prec] uses the working precision prec. |
The abscissas for a 9-point Chebyshev quadrature on a given interval:
| In[1]:= |
| Out[1]= |
Use the specified precision:
| In[2]:= |
| Out[2]= |  |
Use Chebyshev quadrature to approximate the area under a curve:
| In[3]:= |
| Out[3]= |
Plot the curve over a given interval:
| In[4]:= |
| Out[4]= | 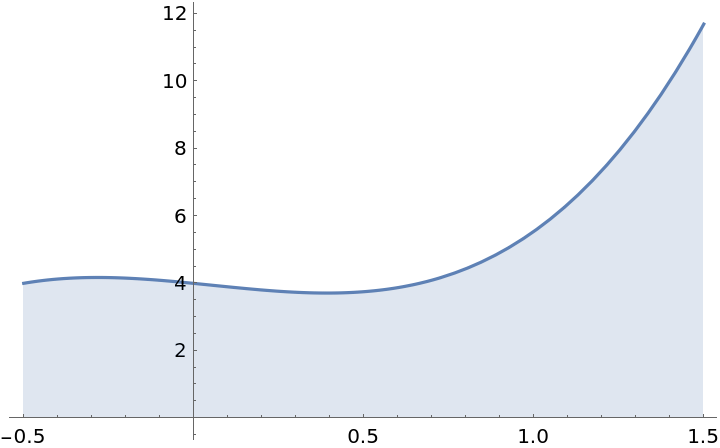 |
Approximate the area under the curve using n-point Chebyshev quadrature:
| In[5]:= |
| In[6]:= |
| Out[6]= |
Compare to the output of NIntegrate:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
Chebyshev abscissas are purely real-valued only for n≤7 and n=9:
| In[9]:= | ![Append[Table[{n, ResourceFunction["ChebyshevQuadratureAbscissas"][n, {-1, 1}]}, {n,
7}], {9, ResourceFunction["ChebyshevQuadratureAbscissas"][
9, {-1, 1}]}] // Column](https://www.wolframcloud.com/obj/resourcesystem/images/c97/c97fa0b0-f649-4de4-8cf1-7cbf01985bd5/27b87f43a208c58a.png) |
| Out[9]= |  |
For other values of n, complex-valued Chebyshev abscissas appear:
| In[10]:= |
| Out[10]= |
Plot the 100-point Chebyshev quadrature abscissas in the complex plane:
| In[11]:= |
| Out[11]= | 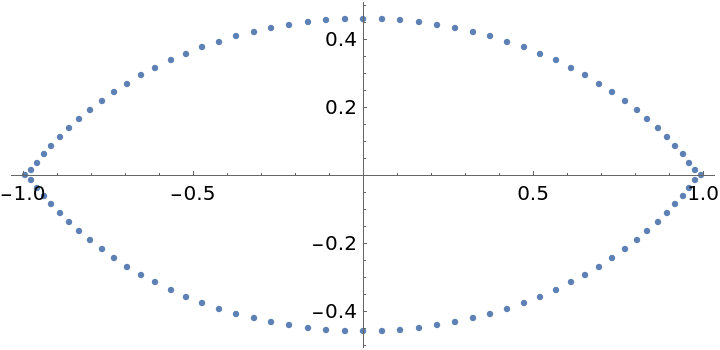 |
This work is licensed under a Creative Commons Attribution 4.0 International License