Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Calculate the value of the second Chebyshev function ψ(x)
ResourceFunction["ChebyshevPsi"][x] returns the value of the second Chebyshev function at x. |
Compute ψ(30):
| In[1]:= |
| Out[1]= |
Obtain a decimal approximation:
| In[2]:= |
| Out[2]= |
Plot ψ(x) from 0 to 30:
| In[3]:= |
| Out[3]= | 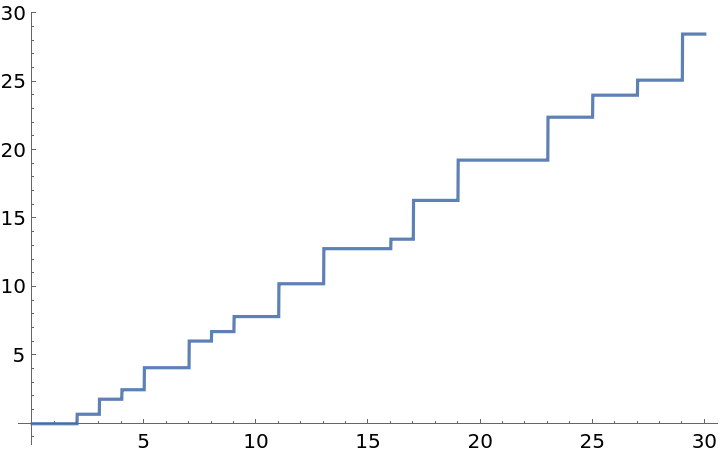 |
Compare x, ψ(x), and |x-ψ(x)|:
| In[4]:= | ![Plot[{x, ResourceFunction["ChebyshevPsi"][x], Abs[x - ResourceFunction["ChebyshevPsi"][x]]}, {x, 0, 30}, PlotLegends -> {"x", "\[Psi](x)", "|x-\[Psi](x)|"}]](https://www.wolframcloud.com/obj/resourcesystem/images/253/25394942-1485-4e5a-bc41-917a0ec50ee5/3927e987e6f47a11.png) |
| Out[4]= | 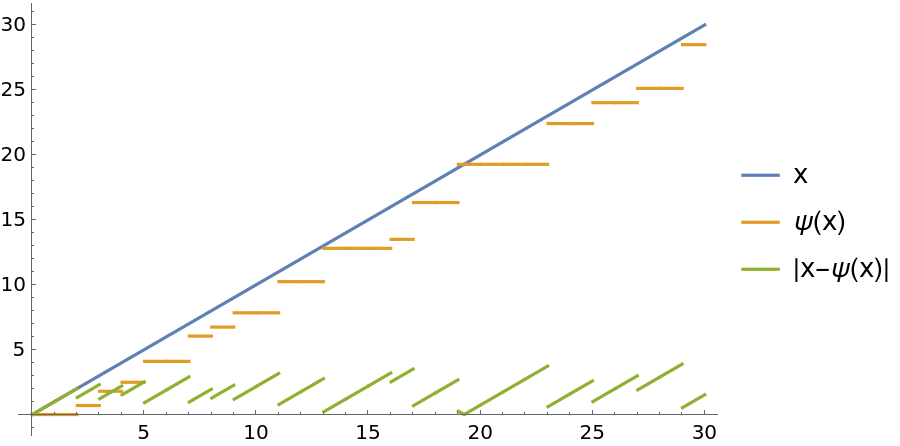 |
Plot the ratio ![]() :
:
| In[5]:= |
| Out[5]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License