Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ChaosGame

Source Notebook

Plot iterations for the 2D chaos game

Contributed by: Eric Weisstein

ResourceFunction["ChaosGame"][n,k,d]

gives k iterations of the 2D chaos game on a regular n-gon with iter points using a ratio of 1/2, dropping the first d points.

ResourceFunction["ChaosGame"][{n,r},k,d]

uses a ratio r.

Details

In a chaos game, one picks a point at random inside a regular n-gon, and then draws the next point a fraction r of the distance between it and a polygon vertex picked at random. The process is continued for k iterations (after throwing out the first d points).

Examples

Basic Examples (1) 

Get three iterations:

In[1]:=
ResourceFunction["ChaosGame"][{5, 1/3}, 3, 0]
Out[1]=

Scope (2) 

Try several geometries:

In[2]:=
GraphicsGrid[ Partition[ Graphics[{PointSize[0.005], Point[ResourceFunction["ChaosGame"][#1, 2000]]}] & /@ {{3, 1/ 2}, {5, 1/3}, {5, 3/8}, {6, 1/3}}, 2]]
Out[2]=

Use more iterations:

In[3]:=
GraphicsGrid[ Partition[ Table[Graphics[{PointSize[0.005], Point[ResourceFunction["ChaosGame"][i, 3*^4]]}], {i, 3, 6}], 2]]
Out[3]=

Increase ratios:

In[4]:=
GraphicsGrid[ Partition[ Graphics[{PointSize[0.005], Point[ResourceFunction["ChaosGame"][{4, #}, 2000]]}] & /@ {0.25, 0.4, 0.5, 0.6, 0.75, 0.9}, 3]]
Out[4]=

Neat Examples (1) 

An animation of the process:

In[5]:=
ChaosGameAnimation[{n_Integer?Positive, r_}, pts_ : 10] := Module[{nf}, Graphics[{ {Directive[PointSize[0.02], Red], Point[CirclePoints[n]]}, MapIndexed[Text[#2[[1]], 0.03 {1, 1} + #1] &, #], Point[#]}] & /@ Reverse[ NestList[Most, ResourceFunction["ChaosGame"][{n, r}, pts, 0], pts]] ]
In[6]:=
ListAnimate[ChaosGameAnimation[{5, 1/3}, 10]]
Out[6]=

Requirements

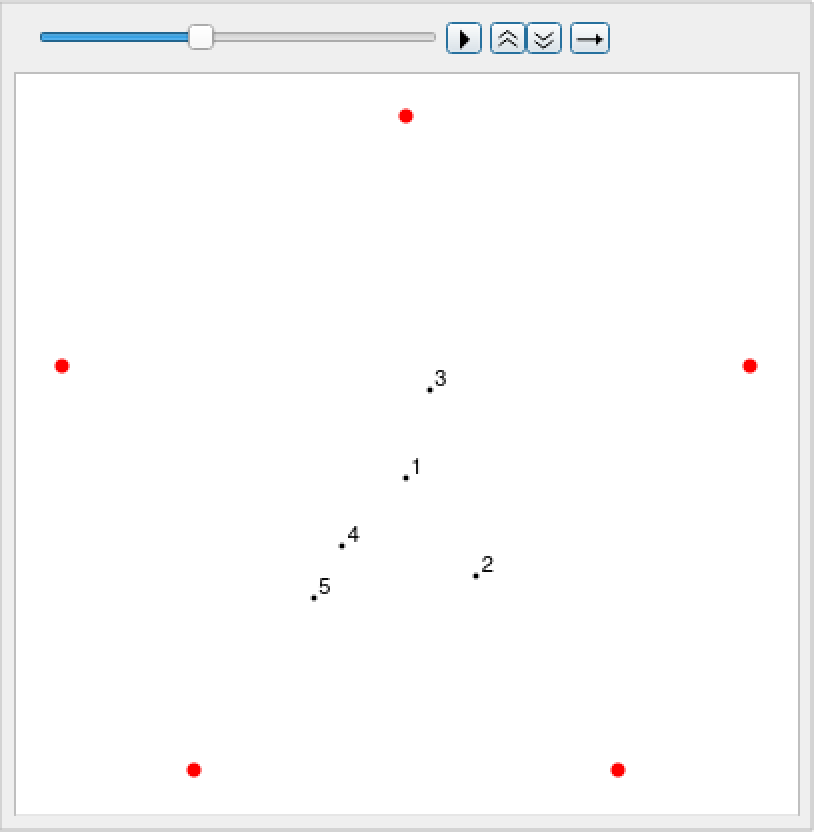Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.1 – 13 September 2021
  • 1.0.0 – 04 March 2019

License Information