Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate an n-sized centering matrix
ResourceFunction["CenteringMatrix"][n] generates an n-sized centering matrix. |
Generate the 3×3 centering matrix:
| In[1]:= |
| Out[1]= |
Center a vector:
| In[2]:= |
| Out[3]= |
Confirm the vector is centered:
| In[4]:= |
| Out[4]= |
Center a matrix column-wise:
| In[5]:= | ![m = Array[RandomInteger[{1, 10}] &, {3, 5}];
mCentered = ResourceFunction["CenteringMatrix"][Length[m]] . m;
MatrixForm[mCentered]](https://www.wolframcloud.com/obj/resourcesystem/images/6fd/6fdd6ee1-1cc0-4402-aaf2-327452d9ea54/3399e7fe7bb8fc16.png) |
| Out[4]= |  |
Confirm the matrix is centered:
| In[6]:= |
| Out[6]= |
Center a matrix row-wise:
| In[7]:= | ![m = Array[RandomInteger[{1, 10}] &, {3, 5}]; mCentered = m . ResourceFunction["CenteringMatrix"][Last[Dimensions[m]]];
MatrixForm[mCentered]](https://www.wolframcloud.com/obj/resourcesystem/images/6fd/6fdd6ee1-1cc0-4402-aaf2-327452d9ea54/05e08825d1ac555c.png) |
| Out[8]= | 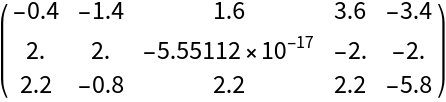 |
Confirm the matrix is centered:
| In[9]:= |
| Out[9]= |
Double center a matrix:
| In[10]:= | ![m = Array[RandomInteger[{1, 10}] &, {3, 5}]; mCentered = ResourceFunction["CenteringMatrix"][Length[m]] . m . ResourceFunction["CenteringMatrix"][Last[Dimensions[m]]];
MatrixForm[mCentered]](https://www.wolframcloud.com/obj/resourcesystem/images/6fd/6fdd6ee1-1cc0-4402-aaf2-327452d9ea54/15d11c5f34dfc5b3.png) |
| Out[11]= |
Confirm the matrix is double centered:
| In[12]:= |
| Out[12]= |
By default WorkingPrecision is set to MachinePrecision:
| In[13]:= |
| Out[13]= |
Compute the 3×3 centering matrix with 2-digit precision:
| In[14]:= |
| Out[14]= |
Compute the 3×3 centering matrix with machine precision:
| In[15]:= |
| Out[15]= |
Compute the 3×3 centering matrix with exact values:
| In[16]:= |
| Out[16]= | 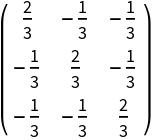 |
By default, CenteringMatrix will return a SparseArray:
| In[17]:= |
| Out[17]= |
Explicitly request a dense matrix from CenteringMatrix:
| In[18]:= |
| Out[18]= |
Define a fictional tabular dataset of species observations by site:
| In[19]:= | ![dataset = Transpose@
Dataset@AssociationThread[
Table["Species " <> ToUpperCase@Alphabet[][[i]], {i, 4}] -> Ceiling@RandomVariate[NormalDistribution[2, 1], {4, 6}]]](https://www.wolframcloud.com/obj/resourcesystem/images/6fd/6fdd6ee1-1cc0-4402-aaf2-327452d9ea54/1450003fc151135e.png) |
| Out[19]= | 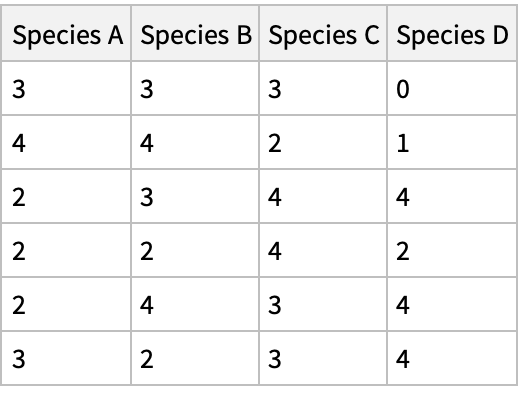 |
Double center the dataset:
| In[20]:= | ![datasetCentered = Module[{keys = Normal[dataset[First, Keys]], values = Normal[Values[dataset]], dims},
dims = Dimensions[values];
values = ResourceFunction["CenteringMatrix"][First[dims]] . values . ResourceFunction["CenteringMatrix"][Last[dims]];
Transpose@Dataset@AssociationThread[keys -> Transpose[values]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/6fd/6fdd6ee1-1cc0-4402-aaf2-327452d9ea54/39801f3b740f6890.png) |
| Out[20]= | 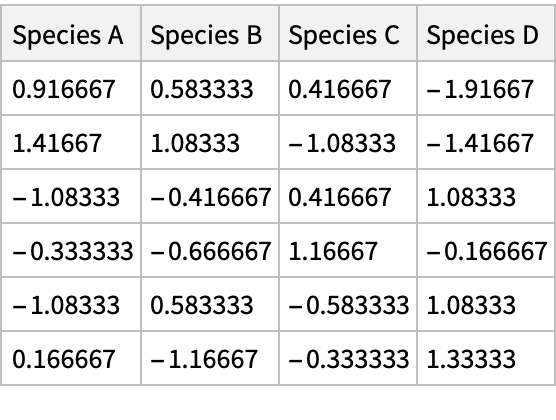 |
Confirm the dataset is double centered:
| In[21]:= |
| Out[21]= |
Define a function to perform PCoA (Classical Multidimensional Scaling) that uses CenteringMatrix:
| In[22]:= | ![ClearAll[PCoA]
PCoA[distanceMatrix_List, dim : _Integer ? Positive : 2] := Module[{centered, c, eigVal, eigVect},
(*Centering matrix*)
c = ResourceFunction["CenteringMatrix"][Length[distanceMatrix], WorkingPrecision -> MachinePrecision];
(*Double centered distance matrix*)
centered = -(1/2) c . distanceMatrix . c;
(*Eigenvalues and eigenvectors*){eigVal, eigVect} = Eigensystem[centered, dim];
(*Coordinates*)
Transpose[eigVect] . Sqrt[DiagonalMatrix[eigVal]] // Re
]](https://www.wolframcloud.com/obj/resourcesystem/images/6fd/6fdd6ee1-1cc0-4402-aaf2-327452d9ea54/40c2e51f4e045b57.png) |
Load the Iris dataset, and create a distance matrix from the data:
| In[23]:= |
Perform PCoA on the distance matrix, and group the reprojected data by species:
| In[24]:= |
Plot the data in sPCoA coordinate space:
| In[25]:= |
| Out[25]= | 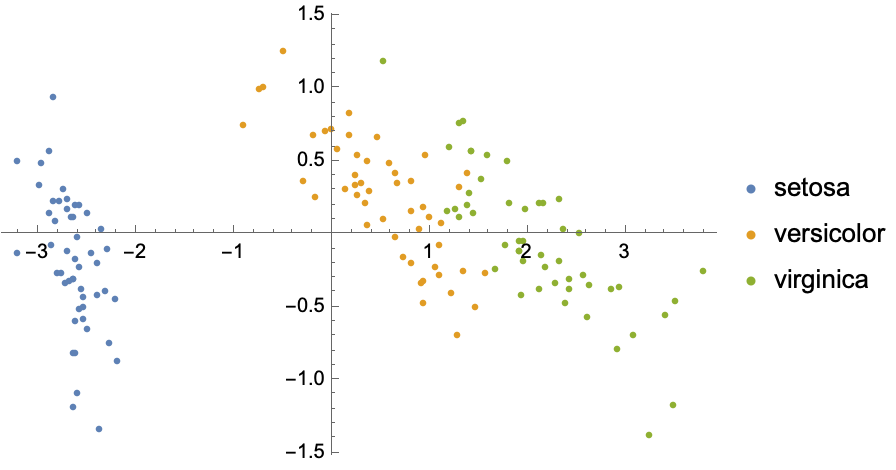 |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License