Basic Examples (3) 

A simplex in 3D, otherwise known as a regular tetrahedron:

In[1]:=

Out[1]=

The center is the origin and all edge-lengths are :

In[2]:=

Out[2]=

Show the simplex:

In[3]:=

Out[3]=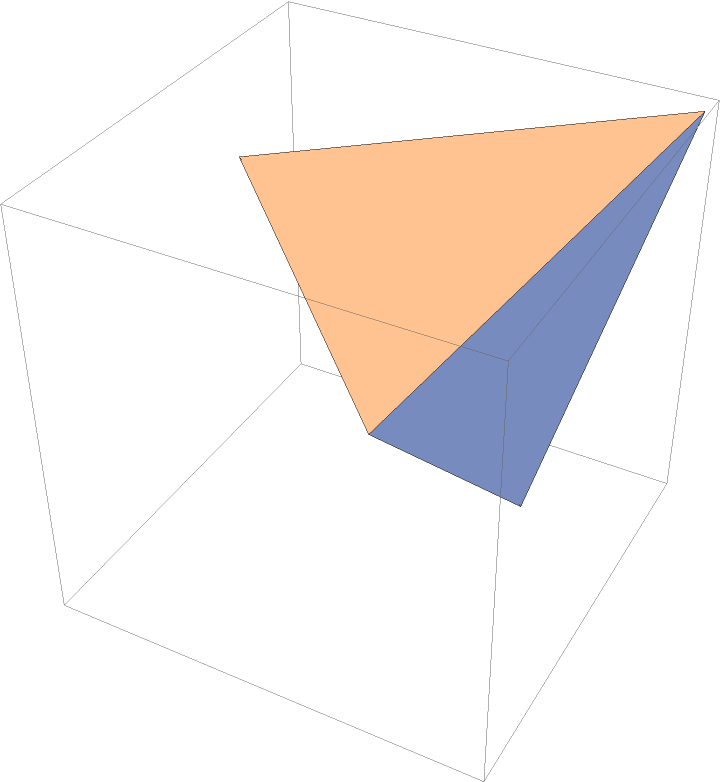

Properties and Relations (2) 

The last vertex of a k-dimensional CenteredSimplex output is a vector of length k with each coordinate having value :

In[4]:=

Out[4]=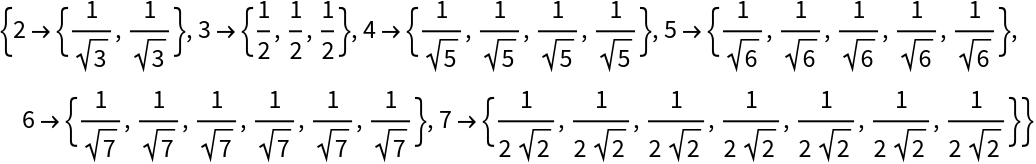

The other k vertices are permutations of one another:

In[5]:=

Out[5]=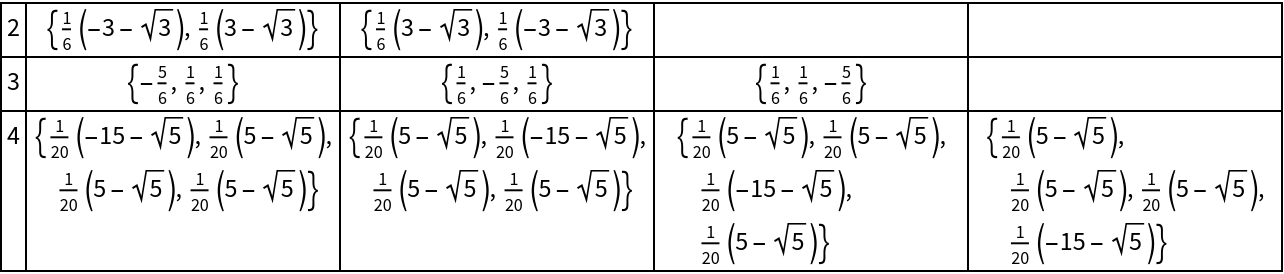

Select two random points in 3D space:

In[6]:=

Out[6]=

We can use the centered simplex system when converting the points to barycentric coordinates, the latter of which can be done using the resource function BarycentricCoordinates:

In[7]:=

Out[7]=

When a regular simplex with edge-lengths is used for barycentric coordinates, the Euclidean distance is preserved:

In[8]:=

Out[8]=

Neat Examples (2) 

We can append to each vertex to get a square matrix:

In[9]:=

Out[9]=

This matrix has determinant 1 as well as mutually orthogonal rows and columns:

In[10]:=

Out[10]=