Basic Examples (4)
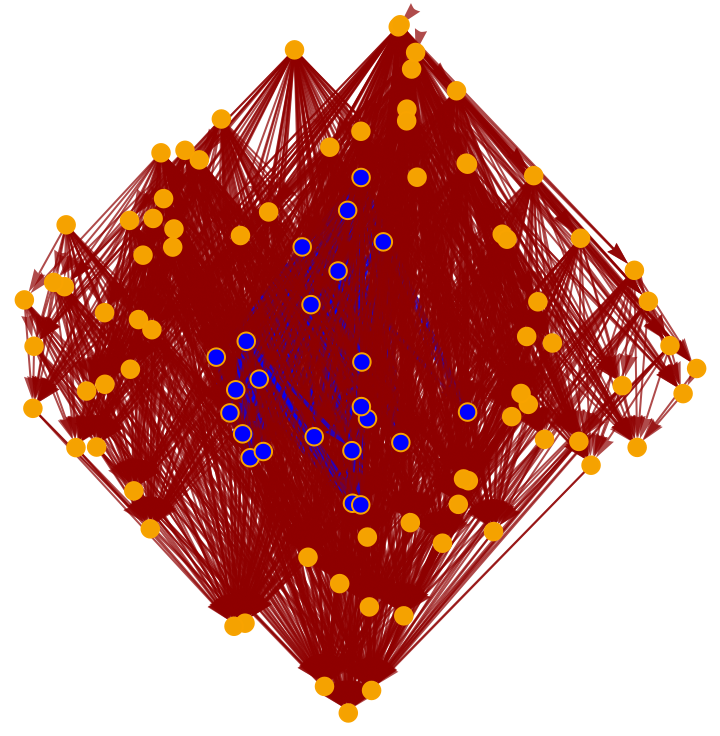
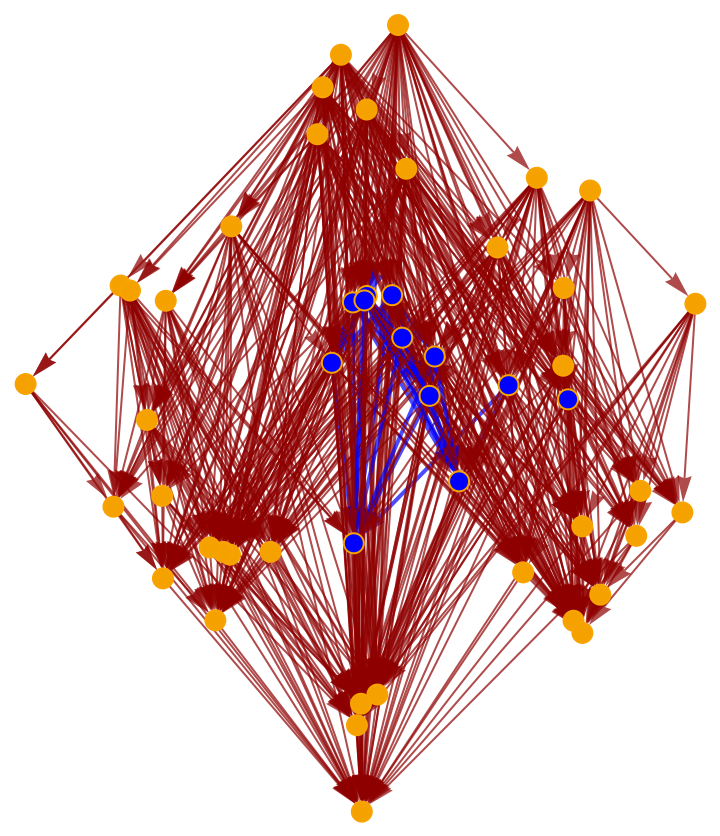
Construct a causal graph by randomly sprinkling 50 points within a diamond-shaped region of 1+1-dimensional Minkowski space:
Construct a subgraph of this causal graph corresponding to a smaller, interior diamond region:
Compute the entanglement entropy associated with this subgraph using the naive approach:
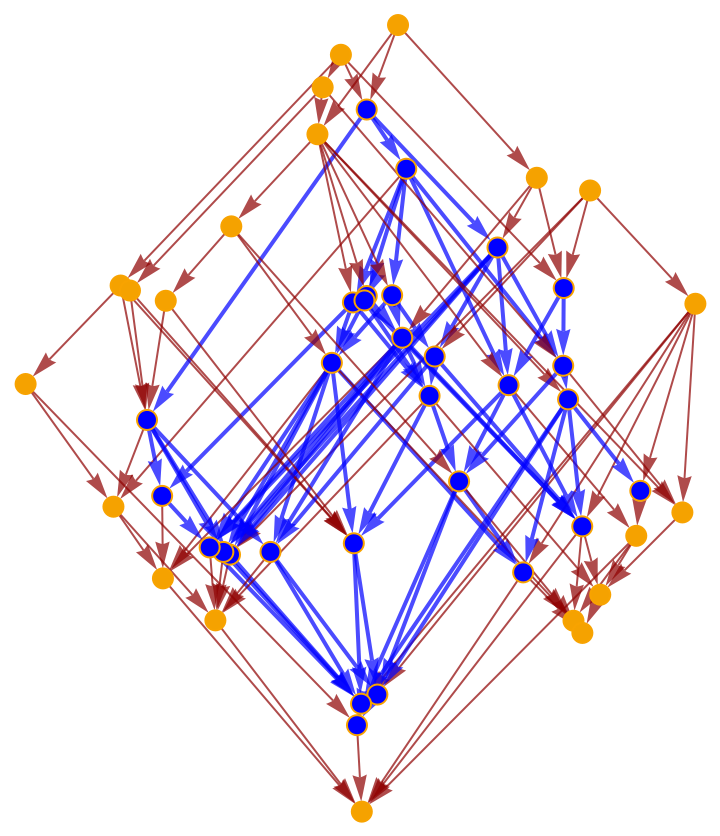
Highlight the interior subgraph within the larger (transitively-reduced) causal graph:
Highlight the interior subgraph within the full (i.e. transitively-closed) causal graph:
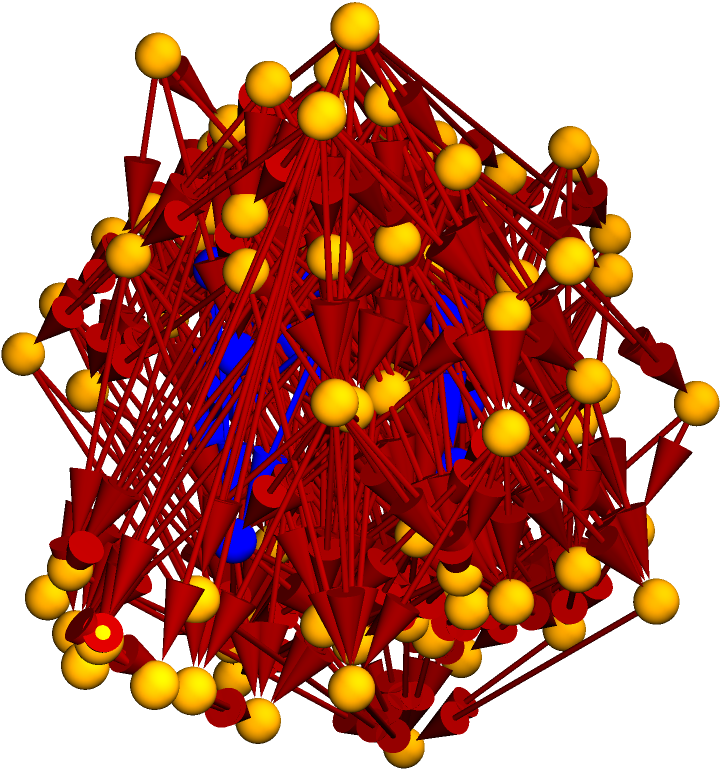
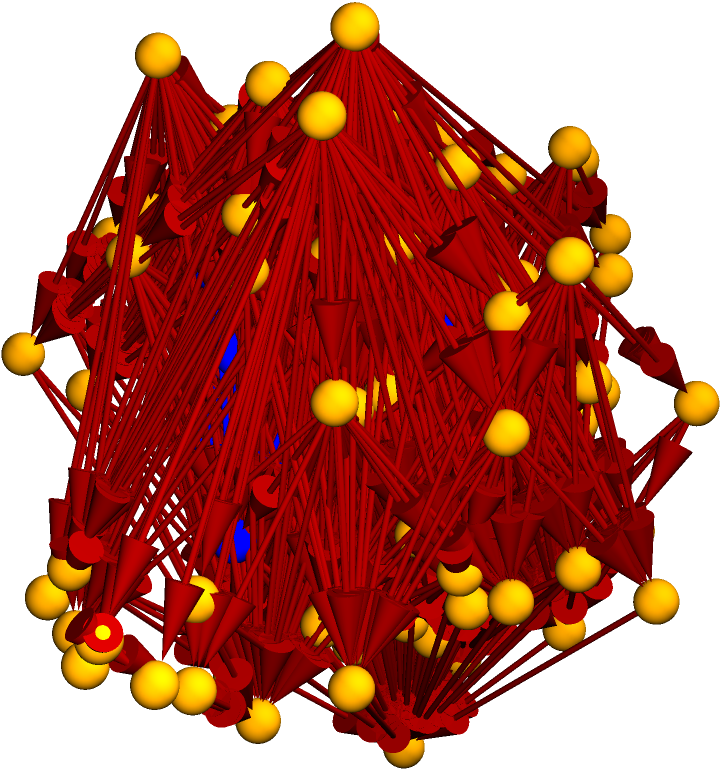
Construct a causal graph by randomly sprinkling 100 points within a diamond-shaped region of 2+1-dimensional Minkowski space:
Construct a subgraph of this causal graph corresponding to a smaller, interior diamond region:
Compute the entanglement entropy associated with this subgraph using the naive approach:
Highlight the interior subgraph within the larger (transitively-reduced) causal graph:
Highlight the interior subgraph within the full (i.e. transitively-closed) causal graph:
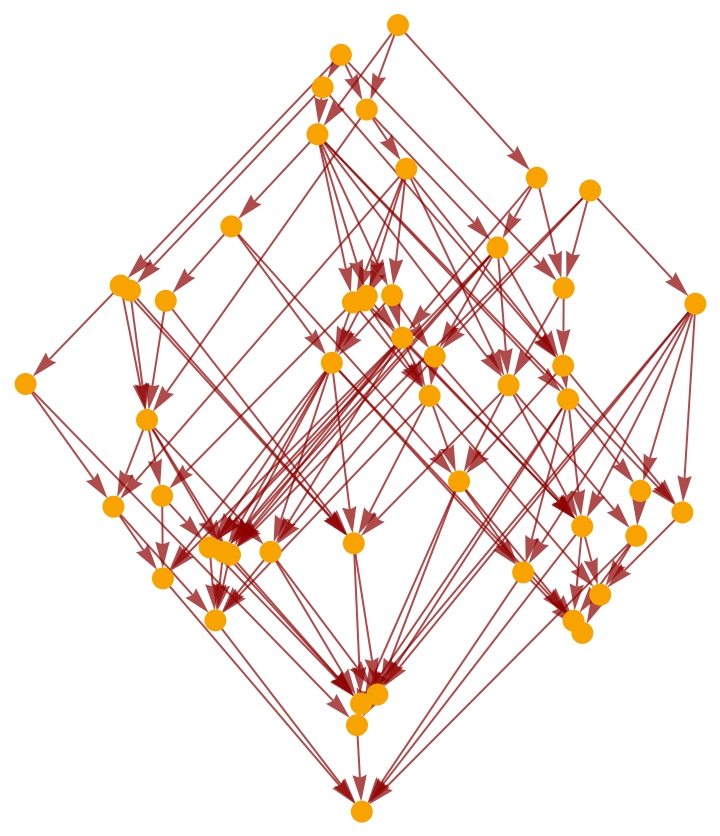
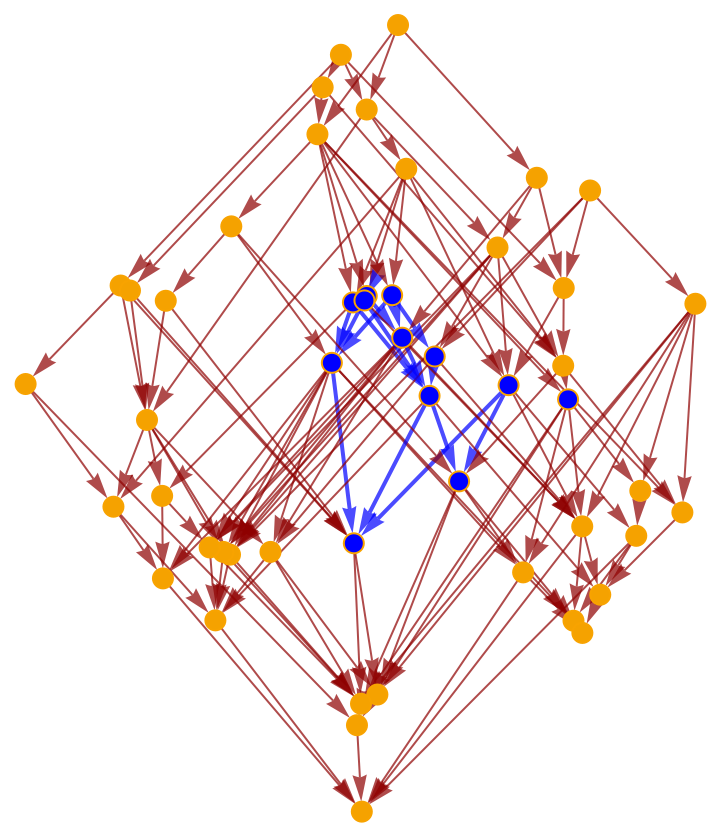
Construct a causal graph by means of a deterministic algorithmic process, e.g. Wolfram model evolution:
Select a random subgraph of the resulting causal graph:
Compute the entanglement entropy associated with this subgraph using the naive approach (note that, when an explicit dimension is not specified, CausalGraphEntanglementEntropyNaive will assume that the dimension of the causal graph is equal to 2):
Compute the entanglement entropy associated with this subgraph using the naive approach, assuming a causal graph dimension of 4 instead (yields an indeterminate result):
Highlight the interior random subgraph within the larger (transitively-reduced) causal graph:
When the Sorkin-Johnston Wightman function (or, equivalently, the Pauli-Jordan operator) of the corresponding causal set is not invertible, CausalGraphEntanglementEntropyNaive will return Indeterminate:
Highlight the interior subgraph within the larger (transitively-reduced) causal graph:
Scope (2)
CausalGraphEntanglementEntropyNaive currently supports the computation of causal set Green's functions (and hence entanglement entropies) in 1+1-dimensions:
2+1-dimensions:
And 3+1-dimensions:
When calling CausalGraphEntanglementEntropyNaive without any property specified, the property "EntanglementEntropy" is assumed by default:
Render the (transitively-reduced) causal graph:
Render the full (i.e. transitively-closed) causal graph instead:
Render the (transitively-reduced) interior subgraph of the overall causal graph:
Render the full (i.e. transitively-closed) interior subgraph of the overall causal graph instead:
Highlight the interior subgraph within the larger (transitively-reduced) causal graph:
Highlight the interior subgraph within the full (i.e. transitively-closed) causal graph instead:
![SeedRandom[100];
causalGraph = ResourceFunction["CurvedSpacetimeRegionSprinkling"][
Abs[x] + Abs[y] < N[(Sqrt[0.5]/2)], {x, y}, {{-0.5, 0.5}, {-0.5, 0.5}}, 50]["CausalGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/392289d2feeaa719.png)
![subgraph = Subgraph[causalGraph, Select[VertexList[causalGraph], Abs[First[#]] + Abs[Last[#]] < N[(Sqrt[0.125]/2)] &]]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/496e29375dd34b26.png)
![SeedRandom[300];
causalGraph = ResourceFunction["CurvedSpacetimeRegionSprinkling"][
Abs[x] + Abs[y] + Abs[z] < N[(Sqrt[0.5]/2)], {x, y, z}, {{-0.5, 0.5}, {-0.5, 0.5}, {-0.5, 0.5}}, 100]["CausalGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/6eb5236676bc1eb9.png)

![subgraph = Subgraph[causalGraph, Select[VertexList[causalGraph], Abs[#[[1]]] + Abs[#[[2]]] + Abs[#[[3]]] < N[(Sqrt[0.125]/2)] &]]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/7f15867226a22930.png)



![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/e93fe0c4-dbe6-468b-8643-054844d18b7a"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/43a6ca808edca11a.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/e3720aee-5332-4b0b-9eeb-db25b2d761f5"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/152c59f64096b2a3.png)
![ResourceFunction["CausalGraphEntanglementEntropyNaive"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
SparseArray[Automatic, {100, 100}, 0, {1, {CompressedData["
1:eJwt0L8rxHEAgOGvcuVX3XAldadOyXAKUVcuXZSSRblFyaWIwXAki5LSTTdY
LDZdBlcWk4nFIFJSyiLdIIPFwKYbeOo+bz3/wNu3slkotURRtBY1i9FOJ3ES
dJMkzQAZBhlmlGyQY4I8k0wzwyxzzLPAIksUWWaVdTYoBVtss8Mue+xzQJkK
hxxxzAlVTjmjxjkXwSVXXHPDLXfBPQ888sQzL8Erb9R554NPvvjmh18a/NFq
ZhsddBEnQQ8peknTT4YhRhgjyzg58kzxD6YDLiw=
"], CompressedData["
1:eJwdj1lTglAAhXFJ3MEIRiVATMRMGzavIoLhQuJUNOCGjGLqe///LXLmPH5n
Y8+/7jkOQZAZg6BIUJJ4elvRdY4nRjhpeUXq4yuerCQbrfaqSDFaUGT6mu2l
0Mf1N6sMJplmoIw31zon+vz4VUXURKPl8bMQ6PlCubOLdaUoy3JDRPWFkYGo
D87xFPFwzrBpzQzSfYIkjoKyuVwF0SFIzPjBrSxTe17uUujAhBlFCwRx5oRF
psn3+nvgAx0uVe0qJoObixJEJYor0Zztzm5kCa9aol+/H6YzF8llpq6kBXA2
N9wiPL1l5cG0Pf5vL5TNySn/0p0famxnOn9fAj+FtlexQlfqNfiWJ4jkJyca
mOyECZR8XMcri42uXK5R+eEG7fGR5QEdAX70ONdZ3GGUDKJZf1lFQCA=
"]}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.032577280450710414`], ArrowBox[CompressedData["
1:eJwVxVmbqQAAAFDZkiUZa4ySQbaotJF9G2FCkSXE1Pv8/7f73fNyiN8/7dft
crkmgMv1f8ALpIAvYAwc3Zi76C67SU/K0/cmvTnv0qv7YF/et/Wpfrff60dB
L1gCq2AdPAbgQD6AB+SACcEQDomQDCmQHvQHkeBn8BTah4kwF5bC0wgUqURM
mINHsAE7SBEpIwxyjZGx0UfroxuPxrsJT6KUqCb0JJmcJ62UkBqkw+lIOpNu
pi8ZIENlWBRDi2gZXaIaamWj2W72mqNz/c9hPprvYglshz2xFz7CDdwpgIVQ
YVhQCIyQiQlhfgW+xFKqlCunys8KXeEqRsWuOCRNMuSumqrmavHasPauJ+vL
RrCBNwqNWmPduDT9TaQpNScUSOEUR8mU2aJbTGve2rWsNtzG25U22ebbYvtG
C/SVEZgBC7IxNssqnSwX5zqcwNM8xxu8zTtiXqRFRuREQ3QkUIpJmFSWFEnr
znt0j+nNe7ueJcfkpJyVl32mfx0WRx+j3jgwhsb2hJ1oU3w6m2ozdibPzAW4
CC5Ci97ivIwuyW/s+7wiVp2VtJopdWW0Bteh9XCtbCKbzGaymW5e2/C2saW2
i5+HWlAJtanO1IX6ra53wu669++RfX1/PACHyIE6sAdeK2mkVtV0ndaZY+74
cyqfmNPQiBsdY2dYZ88ZOefOn+fTxX1BL6uLcR3cuJt9c8yYmTUV83EH7pE7
dWfv/P32SD76j+VDfwrPgRW1BOv6Kr2qL/0dejffq1+fHbfzdscWnLjTcYR/
cYJ+xw==
"], 0.007682766082629425]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.007682766082629425], DiskBox[2, 0.007682766082629425], DiskBox[3, 0.007682766082629425], DiskBox[4, 0.007682766082629425], DiskBox[5, 0.007682766082629425], DiskBox[6, 0.007682766082629425], DiskBox[7, 0.007682766082629425], DiskBox[8, 0.007682766082629425], DiskBox[9, 0.007682766082629425], DiskBox[10, 0.007682766082629425], DiskBox[11, 0.007682766082629425], DiskBox[12, 0.007682766082629425], DiskBox[13, 0.007682766082629425], DiskBox[14, 0.007682766082629425], DiskBox[15, 0.007682766082629425], DiskBox[16, 0.007682766082629425], DiskBox[17, 0.007682766082629425], DiskBox[18, 0.007682766082629425], DiskBox[19, 0.007682766082629425], DiskBox[20, 0.007682766082629425], DiskBox[21, 0.007682766082629425], DiskBox[22, 0.007682766082629425], DiskBox[23, 0.007682766082629425], DiskBox[24, 0.007682766082629425], DiskBox[25, 0.007682766082629425], DiskBox[26, 0.007682766082629425], DiskBox[27, 0.007682766082629425], DiskBox[28, 0.007682766082629425], DiskBox[29, 0.007682766082629425], DiskBox[30, 0.007682766082629425], DiskBox[31, 0.007682766082629425], DiskBox[32, 0.007682766082629425], DiskBox[33, 0.007682766082629425], DiskBox[34, 0.007682766082629425], DiskBox[35, 0.007682766082629425], DiskBox[36, 0.007682766082629425], DiskBox[37, 0.007682766082629425], DiskBox[38, 0.007682766082629425], DiskBox[39, 0.007682766082629425], DiskBox[40, 0.007682766082629425], DiskBox[41, 0.007682766082629425], DiskBox[42, 0.007682766082629425], DiskBox[43, 0.007682766082629425], DiskBox[44, 0.007682766082629425], DiskBox[45, 0.007682766082629425], DiskBox[46, 0.007682766082629425], DiskBox[47, 0.007682766082629425], DiskBox[48, 0.007682766082629425], DiskBox[49, 0.007682766082629425], DiskBox[50, 0.007682766082629425], DiskBox[51, 0.007682766082629425], DiskBox[52, 0.007682766082629425], DiskBox[53, 0.007682766082629425], DiskBox[54, 0.007682766082629425], DiskBox[55, 0.007682766082629425], DiskBox[56, 0.007682766082629425], DiskBox[57, 0.007682766082629425], DiskBox[58, 0.007682766082629425], DiskBox[59, 0.007682766082629425], DiskBox[60, 0.007682766082629425], DiskBox[61, 0.007682766082629425], DiskBox[62, 0.007682766082629425], DiskBox[63, 0.007682766082629425], DiskBox[64, 0.007682766082629425], DiskBox[65, 0.007682766082629425], DiskBox[66, 0.007682766082629425], DiskBox[67, 0.007682766082629425], DiskBox[68, 0.007682766082629425], DiskBox[69, 0.007682766082629425], DiskBox[70, 0.007682766082629425], DiskBox[71, 0.007682766082629425], DiskBox[72, 0.007682766082629425], DiskBox[73, 0.007682766082629425], DiskBox[74, 0.007682766082629425], DiskBox[75, 0.007682766082629425], DiskBox[76, 0.007682766082629425], DiskBox[77, 0.007682766082629425], DiskBox[78, 0.007682766082629425], DiskBox[79, 0.007682766082629425], DiskBox[80, 0.007682766082629425], DiskBox[81, 0.007682766082629425], DiskBox[82, 0.007682766082629425], DiskBox[83, 0.007682766082629425], DiskBox[84, 0.007682766082629425], DiskBox[85, 0.007682766082629425], DiskBox[86, 0.007682766082629425], DiskBox[87, 0.007682766082629425], DiskBox[88, 0.007682766082629425], DiskBox[89, 0.007682766082629425], DiskBox[90, 0.007682766082629425], DiskBox[91, 0.007682766082629425], DiskBox[92, 0.007682766082629425], DiskBox[93, 0.007682766082629425], DiskBox[94, 0.007682766082629425], DiskBox[95, 0.007682766082629425], DiskBox[96, 0.007682766082629425], DiskBox[97, 0.007682766082629425], DiskBox[98, 0.007682766082629425], DiskBox[99, 0.007682766082629425], DiskBox[100, 0.007682766082629425]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
SparseArray[
Automatic, {23, 23}, 0, {1, {{0, 2, 5, 6, 7, 7, 10, 12, 12, 15, 19, 19, 22, 24, 26, 29, 29, 32, 34, 35, 35, 36, 39, 41}, {{5}, {16}, {
1}, {7}, {21}, {13}, {8}, {12}, {14}, {22}, {5}, {16}, {
2}, {3}, {18}, {2}, {3}, {18}, {20}, {3}, {5}, {16}, {
4}, {11}, {9}, {20}, {9}, {12}, {22}, {6}, {10}, {15}, {
7}, {13}, {23}, {19}, {3}, {18}, {23}, {5}, {16}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.04146110156920305], ArrowBox[{1, 5}, 0.0036549079020560286`], ArrowBox[{1, 16}, 0.0036549079020560286`], ArrowBox[{2, 1}, 0.0036549079020560286`], ArrowBox[{2, 7}, 0.0036549079020560286`], ArrowBox[{2, 21}, 0.0036549079020560286`], ArrowBox[{3, 13}, 0.0036549079020560286`], ArrowBox[{4, 8}, 0.0036549079020560286`], ArrowBox[{6, 12}, 0.0036549079020560286`], ArrowBox[{6, 14}, 0.0036549079020560286`], ArrowBox[{6, 22}, 0.0036549079020560286`], ArrowBox[{7, 5}, 0.0036549079020560286`], ArrowBox[{7, 16}, 0.0036549079020560286`], ArrowBox[{9, 2}, 0.0036549079020560286`], ArrowBox[{9, 3}, 0.0036549079020560286`], ArrowBox[{9, 18}, 0.0036549079020560286`], ArrowBox[{10, 2}, 0.0036549079020560286`], ArrowBox[{10, 3}, 0.0036549079020560286`], ArrowBox[{10, 18}, 0.0036549079020560286`], ArrowBox[{10, 20}, 0.0036549079020560286`], ArrowBox[{12, 3}, 0.0036549079020560286`], ArrowBox[{12, 5}, 0.0036549079020560286`], ArrowBox[{12, 16}, 0.0036549079020560286`], ArrowBox[{13, 4}, 0.0036549079020560286`], ArrowBox[{13, 11}, 0.0036549079020560286`], ArrowBox[{14, 9}, 0.0036549079020560286`], ArrowBox[{14, 20}, 0.0036549079020560286`], ArrowBox[{15, 9}, 0.0036549079020560286`], ArrowBox[{15, 12}, 0.0036549079020560286`], ArrowBox[{15, 22}, 0.0036549079020560286`], ArrowBox[{17, 6}, 0.0036549079020560286`], ArrowBox[{17, 10}, 0.0036549079020560286`], ArrowBox[{17, 15}, 0.0036549079020560286`], ArrowBox[{18, 7}, 0.0036549079020560286`], ArrowBox[{18, 13}, 0.0036549079020560286`], ArrowBox[{19, 23}, 0.0036549079020560286`], ArrowBox[{21, 19}, 0.0036549079020560286`], ArrowBox[{22, 3}, 0.0036549079020560286`], ArrowBox[{22, 18}, 0.0036549079020560286`], ArrowBox[{22, 23}, 0.0036549079020560286`], ArrowBox[{23, 5}, 0.0036549079020560286`], ArrowBox[{23, 16}, 0.0036549079020560286`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.0036549079020560286], DiskBox[2, 0.0036549079020560286], DiskBox[3, 0.0036549079020560286], DiskBox[4, 0.0036549079020560286], DiskBox[5, 0.0036549079020560286], DiskBox[6, 0.0036549079020560286], DiskBox[7, 0.0036549079020560286], DiskBox[8, 0.0036549079020560286], DiskBox[9, 0.0036549079020560286], DiskBox[10, 0.0036549079020560286], DiskBox[11, 0.0036549079020560286], DiskBox[12, 0.0036549079020560286], DiskBox[13, 0.0036549079020560286], DiskBox[14, 0.0036549079020560286], DiskBox[15, 0.0036549079020560286], DiskBox[16, 0.0036549079020560286], DiskBox[17, 0.0036549079020560286], DiskBox[18, 0.0036549079020560286], DiskBox[19, 0.0036549079020560286], DiskBox[20, 0.0036549079020560286], DiskBox[21, 0.0036549079020560286], DiskBox[22, 0.0036549079020560286], DiskBox[23, 0.0036549079020560286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), 2]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/0822fbf4c231d015.png)
![ResourceFunction["CausalGraphEntanglementEntropyNaive"][\!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwNlnk8FAgfxq1crURFr5yppKjc5S36ybGJRCKhbK5KbI4Vg3K81JZB7vse
jGtyzBhjGL8x4z7XXY7WsSorOTu2Uq8/vn8/fzzP53keBWcvKzdeHh4e1y22
bZGjsvfa3+Z38VluX2TfBhU/unwNeVxSg/z3WO/2WFdDmMc0r4N/B95XNRfe
8aEc/s7ztkp+5owbKv91IQSVQfbrRezyagKbiNo2W94yoMQUnR9epMPG3fc9
jveLIJVYGG36mYS9O9VlpW6mo86hVmntsTYcltB/2CqUjjySzrvkH3ZghdY7
9mk9Fv7o/Lw9YoQONPenwcLGJOTdGSvAZ0rHruFKb1e9ZkgkhjRtX27FUeLI
IWJVAdx5WWJp4ErDjc39Hr494fDdjvk3oYCDlXM5be6QB8uHzH6VutkPU0Uc
hU8hVRBD3FEuvZeDviLhM2WURjTZ1q18qq4OpRKzfC5db0Mv4doqThMbL0qZ
ztQcjQG9prcZ/GdpIKs5FlJUyADHU0yl0aBKJAbisX9jqmA0ofNgzGoAdlq2
56z194FL6oBs8wcOwHffoLl/WuD3+Uz1qw+TUU0qTByUurEi7pgY/vEAHoyK
Jxv9mgRGWtG2asP+GC5qQwp/0YnRxvq5n+tYqHnljRLVsQhqeAhdq8jASGt+
XSdzJr61YlhJV7nASrWk/uXCy2CT87A3iX8QNRxibcSayBgcYBhyMHAA8sct
x4/bxOPSXyS6w3AXvDGfvC7bnQs7IoJCu8iR0BPD0Fw9TgYvcZ1fPQU5kMYj
mjB/NBMJhNMiToHt0HU6fJZiQEEzW1GhogtV0J9JtUvVaUThnDcfL/7ExhUL
auOieR4ccOa9clywBkjrHgT7c/H4+Hbkn0VqbcBn1r7HZrwYVBV60lKWe2Ah
1OL0t3Qy/C56SOuQaic63oo+Jy7SAKmFA5aKu/PBn3/Fs/NqCp54P7q9Zjwb
v0hu2jYUNqPfvZsPP16Kw9m1+IX2/BaUCz24Y82/Ca1+r7T4ZaUBSm3jpcWi
qFjryLvYTW1BDiHISmyYAufPaXefymJCitzixNP+DKRotSqsr7ZBTZjzv4IS
cWjh+jY3RZKNqx2G09NHEZXJVJVEVhZ2yJTJmE1yUSYgyzMhgIwrc7EcRl4d
CFgEq41V+8Fjt8K0cgEu2GkafUuQr8Fogyg/inkCiFMe5JsNRYH8ml9WViAN
SnZvtnKoTGAtmwR7aSaCAfmGZ+HtZlzfuM56dqcFa0VLLusSaDhu3tv10w0m
+G4K2jrZc7G56bLyyEYZEBKsr5PuU+FtyzgrID8YR4WOmPjHtsH3u07ciWkG
fBkpFxGYzAejjHsyr1YYWOmlUVfU2Qom8xeiOqIrUNg8p4GSXYR8q1+GUhc4
KDv1G2F8qRl2cxTNhQq52HU/1rSfvxrXxC7oitvTkPDKNOLw2HNMThTSvTPJ
Qq1kEkW9go3Dc2/3npSvx8IT+owA6lPIEJO74bKtEUMfUZUFfRgQdjhh5N5c
LOp67nLi29sIrx991FecZmKSaZ7w6+E7aETzqlveylPWgNtSttyWn92ZBF2t
VuR6SOuc6AtFCp/n1FhmKkYttUm6j3WBFDf5WAuNCmcMfg61NmrGofXNKwy9
BGSz+GzzI+rxRVVSNdG4DOZ4JV5J3KmGVjH/P8KP9YJGY/+STnAtZHCSJMkl
0TjmKriZKd8J1RMXuHQmES3oc4freuiYxBVUjpbhooGDvYXJIhPPfoTFlEkO
tgv4nFVUyUP+NauhI6u1KFm+Kryg14h8HV/Fffu8wbg8E0pILVhvTxB8UspE
TYr5mZW8QmBbrXIv70oCtsxHosgIGcQVZLwEBQdAeWlzRDmgAoh3ORsv63rR
WqDzIonih7unxNIr+3PxwLUZOre0ECryj/NVKw9gglr6QndMAxqO1sTWi+Tg
7A9d7TVeJk5r36bkNFBB7C/egVlBGsid+MB2RC6a85SuqXv8ARkORzTtNcnQ
xfJxDR5iQ4nHdOb+70QgO8+ZuRflY7B2DJv/ZhIqpxEXJ+63wvtMMb0fs2n4
8oL9kHRaEsibvr56IK4ZBC4KCewbIqFIs4HIKVcunqVg36AoE/M8Mp97H03B
Co6kt+SVRgj9r23Y6v564G3UUK35QcI8vNT35RodO459Ip9vr0Zjzh7RJFUO
jv/PXFvx25buVVqTr2w3KCn7sKWZNBC41S1zaKt3BnMb5EmkNGD959ugz3EW
XHJ5p52bWwXy7vNTzm71YCSo8tn5RTi2/TQdNKXNRjW5zTNzFzOQ7yH9Q7s6
HXcwJMXn1zjgrV9rxfbNwh5564rKuDoYSa2bF37RhdT17IxEJgObUkte3RIu
wYkkGwdFtyI8OT8bqGVZD+qTH44M+NNgl9mEvnY0GVdfNGbLFFTAj7JIlWMr
/ZD7m7HkXp08qLya2LvcWQQbo9kHSmOZMO9Ud+mLOh3+MdGbiHqQicqv2jom
n7HAj3T6nLJSMeTnBvYE9sVDfpUxPd2kHhfKCEf3r9dDb65qX7F9MrauHviW
erIB3GoNrZb1E3Bip0CcVGgbWjMkTwQLs1Bl1+M/ORKleD4t6revr7jgThiT
e+5Si/Fln6r+lSkB0bBEN5/nLXDVfZjnzR0mKvTw9sifqsLiCZkTUU7x2H7p
lmqYbyQatrxMvc0zhI4PbBtGPApw+Khdwr51MhYs0R5Vva8AVvx0xM0VOmxq
r6vG2cZj8bhd4ZpWB6YwnOv2bu1fu0wt7tR8jjtid47886AUdXhDOhQCmfCz
oKV11RQX2dtvSL+5Yoz+su/Tzw214GSiuENyDxlHDBt5Zoh0yBlUUv109ina
C5pomtUPYu7KuIbx9BOQLM2UWHpLR7xtZDgUUQX5l7+uZni04/jhgHVPqUao
+aq4QBLnQrG/XUVI9dZvePfZpeALEbVIicM9t/+E+pHq5c9CZAhOPejvOx6E
eiPlASdr83HbKaV9jw4O4l8vApSySClwxlIlNXKxG+19VcyF9lViWEFAxGCG
PtjcPEkbkKMhvaCmRJJIQjGZw1f2sPwwmFdRM0StBVrmZmRED3BBQGNES8rq
CV5IvFthlJWOCyqlM8XZNLw2q6NEbClG28Z2usRcHMxonuyvf9IKzquD54zi
GyE7wNsu/Hs1aPxCZUSkZsL/AWMq6S0=
"], {
SparseArray[Automatic, {100, 100}, 0, {1, {CompressedData["
1:eJwt0LErxHEAxuHflcFikckgkrp0pW5wZbKQRR1XhmNBNyk33Il0STFcseoy
6HTpsupXIhlFyqKUK5NiMMpAt3jk+9bzB7yfgaXi7GoiiqJC9L8OOummlz76
GSRJihHSjDLGBFNMB9lghjnyLLBMkRLrbLAZVIItdtnngBqH1DnhlJhzLrni
lmdeeOWNL75pk3Cwix6GSAbDpMgwzmSQJcc8i6zwF6nMGhW22aHKHjWOOKZB
Mzgj5oJrbrjjngcegydavPPBJz/8AsHoMv0=
"], CompressedData["
1:eJwdkN9vmlAUx7ECd4yZVrHWtoCgctUAjTMDlwJSCtVcsVYrost1V+b6vr9/
b7suOQ/nJCffHx/99Of9dMEwzN8Sw9BhZMPJZetxzwLFDOP58lAIDbWl9ZxU
8jKSETWaVRVtsz9fcIGljHCmtQ5QTi7Kn7rfxpOX17e1FxBo2iNfMjykakE0
CxAmnSfZdhO03rHX7Ydk9b7dH44fMMCE06HNZaSCMyLTNcg5UNOcIN6wwBr5
YTxdZgRlFRlGM6xq0SyVICagqcHh+JFGLCTdozEEzFeVVqdn++FTWny5ajTv
W1q7Nxh+f05X2x+cqFucUG8Mcvpevqxf33X7D5PkZfG6PV7e3PbPRUTdsBxe
EGXFMC3HR1hWbJcGLn++umne3nf7w8kzrffrN68cOV3KWF5Uwvlydyg+SkJN
pT3xCWhBjDYAuuMwma93BeXF0WBn5f8kEKWp9+x0dTh5OWkOx2/bvSdb9oj6
nSkGiLDAiKftwQpo0HTDOJlvjgUnwCDHou51kBrlhAdiVYG0/K6QMsEc+bim
OlHOK9Clpie+angZVZLqlFRVMko11WLB5Z3xdeTH08Xyp+ygnHXHyXK9PXCg
osUp/gcnrGiW
"]}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwNlnk8FAgfxq1crURFr5yppKjc5S36ybGJRCKhbK5KbI4Vg3K81JZB7vse
jGtyzBhjGL8x4z7XXY7WsSorOTu2Uq8/vn8/fzzP53keBWcvKzdeHh4e1y22
bZGjsvfa3+Z38VluX2TfBhU/unwNeVxSg/z3WO/2WFdDmMc0r4N/B95XNRfe
8aEc/s7ztkp+5owbKv91IQSVQfbrRezyagKbiNo2W94yoMQUnR9epMPG3fc9
jveLIJVYGG36mYS9O9VlpW6mo86hVmntsTYcltB/2CqUjjySzrvkH3ZghdY7
9mk9Fv7o/Lw9YoQONPenwcLGJOTdGSvAZ0rHruFKb1e9ZkgkhjRtX27FUeLI
IWJVAdx5WWJp4ErDjc39Hr494fDdjvk3oYCDlXM5be6QB8uHzH6VutkPU0Uc
hU8hVRBD3FEuvZeDviLhM2WURjTZ1q18qq4OpRKzfC5db0Mv4doqThMbL0qZ
ztQcjQG9prcZ/GdpIKs5FlJUyADHU0yl0aBKJAbisX9jqmA0ofNgzGoAdlq2
56z194FL6oBs8wcOwHffoLl/WuD3+Uz1qw+TUU0qTByUurEi7pgY/vEAHoyK
Jxv9mgRGWtG2asP+GC5qQwp/0YnRxvq5n+tYqHnljRLVsQhqeAhdq8jASGt+
XSdzJr61YlhJV7nASrWk/uXCy2CT87A3iX8QNRxibcSayBgcYBhyMHAA8sct
x4/bxOPSXyS6w3AXvDGfvC7bnQs7IoJCu8iR0BPD0Fw9TgYvcZ1fPQU5kMYj
mjB/NBMJhNMiToHt0HU6fJZiQEEzW1GhogtV0J9JtUvVaUThnDcfL/7ExhUL
auOieR4ccOa9clywBkjrHgT7c/H4+Hbkn0VqbcBn1r7HZrwYVBV60lKWe2Ah
1OL0t3Qy/C56SOuQaic63oo+Jy7SAKmFA5aKu/PBn3/Fs/NqCp54P7q9Zjwb
v0hu2jYUNqPfvZsPP16Kw9m1+IX2/BaUCz24Y82/Ca1+r7T4ZaUBSm3jpcWi
qFjryLvYTW1BDiHISmyYAufPaXefymJCitzixNP+DKRotSqsr7ZBTZjzv4IS
cWjh+jY3RZKNqx2G09NHEZXJVJVEVhZ2yJTJmE1yUSYgyzMhgIwrc7EcRl4d
CFgEq41V+8Fjt8K0cgEu2GkafUuQr8Fogyg/inkCiFMe5JsNRYH8ml9WViAN
SnZvtnKoTGAtmwR7aSaCAfmGZ+HtZlzfuM56dqcFa0VLLusSaDhu3tv10w0m
+G4K2jrZc7G56bLyyEYZEBKsr5PuU+FtyzgrID8YR4WOmPjHtsH3u07ciWkG
fBkpFxGYzAejjHsyr1YYWOmlUVfU2Qom8xeiOqIrUNg8p4GSXYR8q1+GUhc4
KDv1G2F8qRl2cxTNhQq52HU/1rSfvxrXxC7oitvTkPDKNOLw2HNMThTSvTPJ
Qq1kEkW9go3Dc2/3npSvx8IT+owA6lPIEJO74bKtEUMfUZUFfRgQdjhh5N5c
LOp67nLi29sIrx991FecZmKSaZ7w6+E7aETzqlveylPWgNtSttyWn92ZBF2t
VuR6SOuc6AtFCp/n1FhmKkYttUm6j3WBFDf5WAuNCmcMfg61NmrGofXNKwy9
BGSz+GzzI+rxRVVSNdG4DOZ4JV5J3KmGVjH/P8KP9YJGY/+STnAtZHCSJMkl
0TjmKriZKd8J1RMXuHQmES3oc4freuiYxBVUjpbhooGDvYXJIhPPfoTFlEkO
tgv4nFVUyUP+NauhI6u1KFm+Kryg14h8HV/Fffu8wbg8E0pILVhvTxB8UspE
TYr5mZW8QmBbrXIv70oCtsxHosgIGcQVZLwEBQdAeWlzRDmgAoh3ORsv63rR
WqDzIonih7unxNIr+3PxwLUZOre0ECryj/NVKw9gglr6QndMAxqO1sTWi+Tg
7A9d7TVeJk5r36bkNFBB7C/egVlBGsid+MB2RC6a85SuqXv8ARkORzTtNcnQ
xfJxDR5iQ4nHdOb+70QgO8+ZuRflY7B2DJv/ZhIqpxEXJ+63wvtMMb0fs2n4
8oL9kHRaEsibvr56IK4ZBC4KCewbIqFIs4HIKVcunqVg36AoE/M8Mp97H03B
Co6kt+SVRgj9r23Y6v564G3UUK35QcI8vNT35RodO459Ip9vr0Zjzh7RJFUO
jv/PXFvx25buVVqTr2w3KCn7sKWZNBC41S1zaKt3BnMb5EmkNGD959ugz3EW
XHJ5p52bWwXy7vNTzm71YCSo8tn5RTi2/TQdNKXNRjW5zTNzFzOQ7yH9Q7s6
HXcwJMXn1zjgrV9rxfbNwh5564rKuDoYSa2bF37RhdT17IxEJgObUkte3RIu
wYkkGwdFtyI8OT8bqGVZD+qTH44M+NNgl9mEvnY0GVdfNGbLFFTAj7JIlWMr
/ZD7m7HkXp08qLya2LvcWQQbo9kHSmOZMO9Ud+mLOh3+MdGbiHqQicqv2jom
n7HAj3T6nLJSMeTnBvYE9sVDfpUxPd2kHhfKCEf3r9dDb65qX7F9MrauHviW
erIB3GoNrZb1E3Bip0CcVGgbWjMkTwQLs1Bl1+M/ORKleD4t6revr7jgThiT
e+5Si/Fln6r+lSkB0bBEN5/nLXDVfZjnzR0mKvTw9sifqsLiCZkTUU7x2H7p
lmqYbyQatrxMvc0zhI4PbBtGPApw+Khdwr51MhYs0R5Vva8AVvx0xM0VOmxq
r6vG2cZj8bhd4ZpWB6YwnOv2bu1fu0wt7tR8jjtid47886AUdXhDOhQCmfCz
oKV11RQX2dtvSL+5Yoz+su/Tzw214GSiuENyDxlHDBt5Zoh0yBlUUv109ina
C5pomtUPYu7KuIbx9BOQLM2UWHpLR7xtZDgUUQX5l7+uZni04/jhgHVPqUao
+aq4QBLnQrG/XUVI9dZvePfZpeALEbVIicM9t/+E+pHq5c9CZAhOPejvOx6E
eiPlASdr83HbKaV9jw4O4l8vApSySClwxlIlNXKxG+19VcyF9lViWEFAxGCG
PtjcPEkbkKMhvaCmRJJIQjGZw1f2sPwwmFdRM0StBVrmZmRED3BBQGNES8rq
CV5IvFthlJWOCyqlM8XZNLw2q6NEbClG28Z2usRcHMxonuyvf9IKzquD54zi
GyE7wNsu/Hs1aPxCZUSkZsL/AWMq6S0=
"]}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJwNlnk8FAgfxq1crURFr5yppKjc5S36ybGJRCKhbK5KbI4Vg3K81JZB7vse
jGtyzBhjGL8x4z7XXY7WsSorOTu2Uq8/vn8/fzzP53keBWcvKzdeHh4e1y22
bZGjsvfa3+Z38VluX2TfBhU/unwNeVxSg/z3WO/2WFdDmMc0r4N/B95XNRfe
8aEc/s7ztkp+5owbKv91IQSVQfbrRezyagKbiNo2W94yoMQUnR9epMPG3fc9
jveLIJVYGG36mYS9O9VlpW6mo86hVmntsTYcltB/2CqUjjySzrvkH3ZghdY7
9mk9Fv7o/Lw9YoQONPenwcLGJOTdGSvAZ0rHruFKb1e9ZkgkhjRtX27FUeLI
IWJVAdx5WWJp4ErDjc39Hr494fDdjvk3oYCDlXM5be6QB8uHzH6VutkPU0Uc
hU8hVRBD3FEuvZeDviLhM2WURjTZ1q18qq4OpRKzfC5db0Mv4doqThMbL0qZ
ztQcjQG9prcZ/GdpIKs5FlJUyADHU0yl0aBKJAbisX9jqmA0ofNgzGoAdlq2
56z194FL6oBs8wcOwHffoLl/WuD3+Uz1qw+TUU0qTByUurEi7pgY/vEAHoyK
Jxv9mgRGWtG2asP+GC5qQwp/0YnRxvq5n+tYqHnljRLVsQhqeAhdq8jASGt+
XSdzJr61YlhJV7nASrWk/uXCy2CT87A3iX8QNRxibcSayBgcYBhyMHAA8sct
x4/bxOPSXyS6w3AXvDGfvC7bnQs7IoJCu8iR0BPD0Fw9TgYvcZ1fPQU5kMYj
mjB/NBMJhNMiToHt0HU6fJZiQEEzW1GhogtV0J9JtUvVaUThnDcfL/7ExhUL
auOieR4ccOa9clywBkjrHgT7c/H4+Hbkn0VqbcBn1r7HZrwYVBV60lKWe2Ah
1OL0t3Qy/C56SOuQaic63oo+Jy7SAKmFA5aKu/PBn3/Fs/NqCp54P7q9Zjwb
v0hu2jYUNqPfvZsPP16Kw9m1+IX2/BaUCz24Y82/Ca1+r7T4ZaUBSm3jpcWi
qFjryLvYTW1BDiHISmyYAufPaXefymJCitzixNP+DKRotSqsr7ZBTZjzv4IS
cWjh+jY3RZKNqx2G09NHEZXJVJVEVhZ2yJTJmE1yUSYgyzMhgIwrc7EcRl4d
CFgEq41V+8Fjt8K0cgEu2GkafUuQr8Fogyg/inkCiFMe5JsNRYH8ml9WViAN
SnZvtnKoTGAtmwR7aSaCAfmGZ+HtZlzfuM56dqcFa0VLLusSaDhu3tv10w0m
+G4K2jrZc7G56bLyyEYZEBKsr5PuU+FtyzgrID8YR4WOmPjHtsH3u07ciWkG
fBkpFxGYzAejjHsyr1YYWOmlUVfU2Qom8xeiOqIrUNg8p4GSXYR8q1+GUhc4
KDv1G2F8qRl2cxTNhQq52HU/1rSfvxrXxC7oitvTkPDKNOLw2HNMThTSvTPJ
Qq1kEkW9go3Dc2/3npSvx8IT+owA6lPIEJO74bKtEUMfUZUFfRgQdjhh5N5c
LOp67nLi29sIrx991FecZmKSaZ7w6+E7aETzqlveylPWgNtSttyWn92ZBF2t
VuR6SOuc6AtFCp/n1FhmKkYttUm6j3WBFDf5WAuNCmcMfg61NmrGofXNKwy9
BGSz+GzzI+rxRVVSNdG4DOZ4JV5J3KmGVjH/P8KP9YJGY/+STnAtZHCSJMkl
0TjmKriZKd8J1RMXuHQmES3oc4freuiYxBVUjpbhooGDvYXJIhPPfoTFlEkO
tgv4nFVUyUP+NauhI6u1KFm+Kryg14h8HV/Fffu8wbg8E0pILVhvTxB8UspE
TYr5mZW8QmBbrXIv70oCtsxHosgIGcQVZLwEBQdAeWlzRDmgAoh3ORsv63rR
WqDzIonih7unxNIr+3PxwLUZOre0ECryj/NVKw9gglr6QndMAxqO1sTWi+Tg
7A9d7TVeJk5r36bkNFBB7C/egVlBGsid+MB2RC6a85SuqXv8ARkORzTtNcnQ
xfJxDR5iQ4nHdOb+70QgO8+ZuRflY7B2DJv/ZhIqpxEXJ+63wvtMMb0fs2n4
8oL9kHRaEsibvr56IK4ZBC4KCewbIqFIs4HIKVcunqVg36AoE/M8Mp97H03B
Co6kt+SVRgj9r23Y6v564G3UUK35QcI8vNT35RodO459Ip9vr0Zjzh7RJFUO
jv/PXFvx25buVVqTr2w3KCn7sKWZNBC41S1zaKt3BnMb5EmkNGD959ugz3EW
XHJ5p52bWwXy7vNTzm71YCSo8tn5RTi2/TQdNKXNRjW5zTNzFzOQ7yH9Q7s6
HXcwJMXn1zjgrV9rxfbNwh5564rKuDoYSa2bF37RhdT17IxEJgObUkte3RIu
wYkkGwdFtyI8OT8bqGVZD+qTH44M+NNgl9mEvnY0GVdfNGbLFFTAj7JIlWMr
/ZD7m7HkXp08qLya2LvcWQQbo9kHSmOZMO9Ud+mLOh3+MdGbiHqQicqv2jom
n7HAj3T6nLJSMeTnBvYE9sVDfpUxPd2kHhfKCEf3r9dDb65qX7F9MrauHviW
erIB3GoNrZb1E3Bip0CcVGgbWjMkTwQLs1Bl1+M/ORKleD4t6revr7jgThiT
e+5Si/Fln6r+lSkB0bBEN5/nLXDVfZjnzR0mKvTw9sifqsLiCZkTUU7x2H7p
lmqYbyQatrxMvc0zhI4PbBtGPApw+Khdwr51MhYs0R5Vva8AVvx0xM0VOmxq
r6vG2cZj8bhd4ZpWB6YwnOv2bu1fu0wt7tR8jjtid47886AUdXhDOhQCmfCz
oKV11RQX2dtvSL+5Yoz+su/Tzw214GSiuENyDxlHDBt5Zoh0yBlUUv109ina
C5pomtUPYu7KuIbx9BOQLM2UWHpLR7xtZDgUUQX5l7+uZni04/jhgHVPqUao
+aq4QBLnQrG/XUVI9dZvePfZpeALEbVIicM9t/+E+pHq5c9CZAhOPejvOx6E
eiPlASdr83HbKaV9jw4O4l8vApSySClwxlIlNXKxG+19VcyF9lViWEFAxGCG
PtjcPEkbkKMhvaCmRJJIQjGZw1f2sPwwmFdRM0StBVrmZmRED3BBQGNES8rq
CV5IvFthlJWOCyqlM8XZNLw2q6NEbClG28Z2usRcHMxonuyvf9IKzquD54zi
GyE7wNsu/Hs1aPxCZUSkZsL/AWMq6S0=
"], {
{Hue[0, 1, 0.56], Arrowheads[0.04653118453936606], Arrow3DBox[TubeBox[CompressedData["
1:eJwVxdt/gQoAAOBRiZlrY3KP5JZCI42KSpRLTIVFhPfz95+38zvfy4c9/vl9
+N/e3v71vb39vy/vq/kGPtuf95P+H/8JAAEYKABtQARkQAe2wAW4gyEwDRbB
ElgG6+AAXEEINIZMyA2YARcuwjN4EUwEC8Fy8BA8hZDQOGSG3Hfiff3uhJGw
GXY/oI/2B/mxj/ARLWJH3Kg/CkSDUTz6HWWjQnQe3USN6D42jvExN07E2/FO
vB+fJJFkLTn+1FLFVDnFp2apRZpPa2kn7X5Vv6aZfKaTGWaUjJbZZ44oiKbQ
CkqhCrpDf1ELPaEX9Ia+skSWzzpZNwflsByR6+ShgllwS5GSg5mYW8lXsApR
6VT4il2FqnA1WS1XB1W+KlcPOIjDOIn38Qku4jKu4tuaWXMJjTDrkXq+TtRn
9UXdaRQb5cassWismkiTaDpNtwW3Mq1yi2h1W2zrpyW25JbeureRNtYekwhp
km4n1HGoAJWgClSJqlJ1qkNNKJGaUivqTn/QcTpNZ+gcXaLLdIWu0026S49o
iV7RO9qiz12oG+5iXbIH9UK9z1661+zZfaSP9ccMwMSYTybFZBmcaTAUIzAK
M2fWzIaxmNt37PvrG/1uDJCBOXCH0DA8xIa1ITkcsAE2xIbZPFtga2ybJdkB
O2E11hnlR4VRZzQcaaP96MgB3DsX5764DIdyOQ7nGlyXEziJm3MbzuA87vkT
+Cn83CbQBOMR3hRAISCEhYIgCrqwFY7CRbgLL9EnhsSkWBR5cSYuREd8TOFp
ecpP5ak2PUiwREhDiZVESZF0aS8dpbtclGfyQoGUgJJQCgqm1BRSGcyL8/Kc
n8/mi7mmptWiWlIxta521JW6Uy/qYzFe2At3mVl2l+zSWFrLkzbW8zqpd/S+
PtAnurbiV9rKXrlrfq2t3Q24gTe1jbxRt5Vtc7szYKNsEEbbGBqiIRuKoRsH
42bcd9AutCN2/M7eOfvwHtuPf6u/2qF4mB3sg2sFLNgKWwmrYBGWaMmWbh2t
u43Y5jF0bB/7x8nROSVPxdPgNDvZ58C5cCbOw7N+3p+P58df4C/xV3PGjnnh
L9rFvSLXzytxda7uLXFDbrW77568F++kB3qwF/OyXs3reX1v4sme6q29rXd9
5B+Dh/awn+Bz+GSfynP73D+t5+UFveBX5FV+ya/Vy/kPV3bQHw==
"]], 0.014399619678830035`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], SphereBox[1, 0.014399619678830035`], SphereBox[2, 0.014399619678830035`], SphereBox[3, 0.014399619678830035`], SphereBox[4, 0.014399619678830035`], SphereBox[5, 0.014399619678830035`], SphereBox[6, 0.014399619678830035`], SphereBox[7, 0.014399619678830035`], SphereBox[8, 0.014399619678830035`], SphereBox[9, 0.014399619678830035`], SphereBox[10, 0.014399619678830035`], SphereBox[11, 0.014399619678830035`], SphereBox[12, 0.014399619678830035`], SphereBox[13, 0.014399619678830035`], SphereBox[14, 0.014399619678830035`], SphereBox[15, 0.014399619678830035`], SphereBox[16, 0.014399619678830035`], SphereBox[17, 0.014399619678830035`], SphereBox[18, 0.014399619678830035`], SphereBox[19, 0.014399619678830035`], SphereBox[20, 0.014399619678830035`], SphereBox[21, 0.014399619678830035`], SphereBox[22, 0.014399619678830035`], SphereBox[23, 0.014399619678830035`], SphereBox[24, 0.014399619678830035`], SphereBox[25, 0.014399619678830035`], SphereBox[26, 0.014399619678830035`], SphereBox[27, 0.014399619678830035`], SphereBox[28, 0.014399619678830035`], SphereBox[29, 0.014399619678830035`], SphereBox[30, 0.014399619678830035`], SphereBox[31, 0.014399619678830035`], SphereBox[32, 0.014399619678830035`], SphereBox[33, 0.014399619678830035`], SphereBox[34, 0.014399619678830035`], SphereBox[35, 0.014399619678830035`], SphereBox[36, 0.014399619678830035`], SphereBox[37, 0.014399619678830035`], SphereBox[38, 0.014399619678830035`], SphereBox[39, 0.014399619678830035`], SphereBox[40, 0.014399619678830035`], SphereBox[41, 0.014399619678830035`], SphereBox[42, 0.014399619678830035`], SphereBox[43, 0.014399619678830035`], SphereBox[44, 0.014399619678830035`], SphereBox[45, 0.014399619678830035`], SphereBox[46, 0.014399619678830035`], SphereBox[47, 0.014399619678830035`], SphereBox[48, 0.014399619678830035`], SphereBox[49, 0.014399619678830035`], SphereBox[50, 0.014399619678830035`], SphereBox[51, 0.014399619678830035`], SphereBox[52, 0.014399619678830035`], SphereBox[53, 0.014399619678830035`], SphereBox[54, 0.014399619678830035`], SphereBox[55, 0.014399619678830035`], SphereBox[56, 0.014399619678830035`], SphereBox[57, 0.014399619678830035`], SphereBox[58, 0.014399619678830035`], SphereBox[59, 0.014399619678830035`], SphereBox[60, 0.014399619678830035`], SphereBox[61, 0.014399619678830035`], SphereBox[62, 0.014399619678830035`], SphereBox[63, 0.014399619678830035`], SphereBox[64, 0.014399619678830035`], SphereBox[65, 0.014399619678830035`], SphereBox[66, 0.014399619678830035`], SphereBox[67, 0.014399619678830035`], SphereBox[68, 0.014399619678830035`], SphereBox[69, 0.014399619678830035`], SphereBox[70, 0.014399619678830035`], SphereBox[71, 0.014399619678830035`], SphereBox[72, 0.014399619678830035`], SphereBox[73, 0.014399619678830035`], SphereBox[74, 0.014399619678830035`], SphereBox[75, 0.014399619678830035`], SphereBox[76, 0.014399619678830035`], SphereBox[77, 0.014399619678830035`], SphereBox[78, 0.014399619678830035`], SphereBox[79, 0.014399619678830035`], SphereBox[80, 0.014399619678830035`], SphereBox[81, 0.014399619678830035`], SphereBox[82, 0.014399619678830035`], SphereBox[83, 0.014399619678830035`], SphereBox[84, 0.014399619678830035`], SphereBox[85, 0.014399619678830035`], SphereBox[86, 0.014399619678830035`], SphereBox[87, 0.014399619678830035`], SphereBox[88, 0.014399619678830035`], SphereBox[89, 0.014399619678830035`], SphereBox[90, 0.014399619678830035`], SphereBox[91, 0.014399619678830035`], SphereBox[92, 0.014399619678830035`], SphereBox[93, 0.014399619678830035`], SphereBox[94, 0.014399619678830035`], SphereBox[95, 0.014399619678830035`], SphereBox[96, 0.014399619678830035`], SphereBox[97, 0.014399619678830035`], SphereBox[98, 0.014399619678830035`], SphereBox[99, 0.014399619678830035`], SphereBox[100, 0.014399619678830035`]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
Boxed->False,
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}}]\), \!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBmQJm/SFib1JlAgAAABsAAAADAAAAnisWWORNar+Pn86EzvSzv/Zj+36G
qLK/5KBwUpWPYr/0KzljeHqqP53m67/Kb74/1BVAfcUImb8AGGIRH33Iv6w0
7MA6Pb2//8n4CYPVtj+0aYl7C0WjvwIOjgYESra/jYsMqxsWwr9yDYHhqq28
v0gDyyo3t7e/RDSMVzDUdr+BD1WjgdjJv4xFQJ/4t72/M1PnJ7NepT+yAHjK
8b+4v4RUBTxhTbq/dgXwbMlWlr8u7tYJstqdv/oY/Ve7pMG/dG5gffZOkL/i
8pHpx6HEvx5/Iwzydr6/HHecbJJ3p7/w447CuKC3PwZPezDXsXQ/ve9Ie28z
kz9Cp11spGfBv/P0XL2PaMS/wb5RKtX0qj94klRco3WzP+jE2r13oXu/C02e
u62dpb8E8frTl+nCvx3dbXja7cE/EsIlTQikw7/KdY5KzwWxv/IQSTwUWrS/
eN5KgybXrr+Vkwg8aNy9vzSVo60xrMC/sdtJw7a6i79PtuMmt8y2v5TDByqM
HMO/qGvgmyD+iz+nYuNLaaWhv3s1jcAFYJS/KpiL69t1xT/umxA9/+KYv9lJ
WtMbmJQ/fzlXgPEguT8CvDIvsv+jv6C/Ts76WLa/MB79O+NMmr8Efbb1xzG2
vwy4GBTl8sI/s/OdmpO6uL++l6jeZguov9uUVVslZaW/oZ95zHnOkT+hsEW2
mUi5v+mqeCkg87k/zZ8vzqZalb/F8SL8lza7P2W1Q1LvQJK/XnxXu9Vror/U
KVmSGfOnv6LttIWw7qw/lrhitxa+wL/HHLW/DjOuvwyODtXqfKm/gKJ3g9Ka
QD9VYDa00R60v7aisqgYi6O/BjLVNBpSiL9Jk2qsRJyZv+krqeGmnbS/OyVk
vw==
"], {
SparseArray[
Automatic, {27, 27}, 0, {1, {{0, 3, 10, 10, 10, 10, 10, 11, 11, 11, 12, 12, 13, 18, 18, 18, 18, 21, 23, 23, 25, 28, 34, 34, 44, 45, 48, 50}, {{8}, {11}, {16}, {4}, {9}, {14}, {17}, {19}, {21}, {
26}, {11}, {8}, {8}, {4}, {17}, {19}, {21}, {26}, {1}, {
7}, {27}, {4}, {19}, {22}, {24}, {8}, {15}, {16}, {4}, {
14}, {17}, {19}, {21}, {26}, {3}, {4}, {5}, {6}, {9}, {
17}, {19}, {21}, {25}, {26}, {14}, {1}, {7}, {15}, {8}, {
16}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwBmQJm/SFib1JlAgAAABsAAAADAAAAnisWWORNar+Pn86EzvSzv/Zj+36G
qLK/5KBwUpWPYr/0KzljeHqqP53m67/Kb74/1BVAfcUImb8AGGIRH33Iv6w0
7MA6Pb2//8n4CYPVtj+0aYl7C0WjvwIOjgYESra/jYsMqxsWwr9yDYHhqq28
v0gDyyo3t7e/RDSMVzDUdr+BD1WjgdjJv4xFQJ/4t72/M1PnJ7NepT+yAHjK
8b+4v4RUBTxhTbq/dgXwbMlWlr8u7tYJstqdv/oY/Ve7pMG/dG5gffZOkL/i
8pHpx6HEvx5/Iwzydr6/HHecbJJ3p7/w447CuKC3PwZPezDXsXQ/ve9Ie28z
kz9Cp11spGfBv/P0XL2PaMS/wb5RKtX0qj94klRco3WzP+jE2r13oXu/C02e
u62dpb8E8frTl+nCvx3dbXja7cE/EsIlTQikw7/KdY5KzwWxv/IQSTwUWrS/
eN5KgybXrr+Vkwg8aNy9vzSVo60xrMC/sdtJw7a6i79PtuMmt8y2v5TDByqM
HMO/qGvgmyD+iz+nYuNLaaWhv3s1jcAFYJS/KpiL69t1xT/umxA9/+KYv9lJ
WtMbmJQ/fzlXgPEguT8CvDIvsv+jv6C/Ts76WLa/MB79O+NMmr8Efbb1xzG2
vwy4GBTl8sI/s/OdmpO6uL++l6jeZguov9uUVVslZaW/oZ95zHnOkT+hsEW2
mUi5v+mqeCkg87k/zZ8vzqZalb/F8SL8lza7P2W1Q1LvQJK/XnxXu9Vror/U
KVmSGfOnv6LttIWw7qw/lrhitxa+wL/HHLW/DjOuvwyODtXqfKm/gKJ3g9Ka
QD9VYDa00R60v7aisqgYi6O/BjLVNBpSiL9Jk2qsRJyZv+krqeGmnbS/OyVk
vw==
"]}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJwBmQJm/SFib1JlAgAAABsAAAADAAAAnisWWORNar+Pn86EzvSzv/Zj+36G
qLK/5KBwUpWPYr/0KzljeHqqP53m67/Kb74/1BVAfcUImb8AGGIRH33Iv6w0
7MA6Pb2//8n4CYPVtj+0aYl7C0WjvwIOjgYESra/jYsMqxsWwr9yDYHhqq28
v0gDyyo3t7e/RDSMVzDUdr+BD1WjgdjJv4xFQJ/4t72/M1PnJ7NepT+yAHjK
8b+4v4RUBTxhTbq/dgXwbMlWlr8u7tYJstqdv/oY/Ve7pMG/dG5gffZOkL/i
8pHpx6HEvx5/Iwzydr6/HHecbJJ3p7/w447CuKC3PwZPezDXsXQ/ve9Ie28z
kz9Cp11spGfBv/P0XL2PaMS/wb5RKtX0qj94klRco3WzP+jE2r13oXu/C02e
u62dpb8E8frTl+nCvx3dbXja7cE/EsIlTQikw7/KdY5KzwWxv/IQSTwUWrS/
eN5KgybXrr+Vkwg8aNy9vzSVo60xrMC/sdtJw7a6i79PtuMmt8y2v5TDByqM
HMO/qGvgmyD+iz+nYuNLaaWhv3s1jcAFYJS/KpiL69t1xT/umxA9/+KYv9lJ
WtMbmJQ/fzlXgPEguT8CvDIvsv+jv6C/Ts76WLa/MB79O+NMmr8Efbb1xzG2
vwy4GBTl8sI/s/OdmpO6uL++l6jeZguov9uUVVslZaW/oZ95zHnOkT+hsEW2
mUi5v+mqeCkg87k/zZ8vzqZalb/F8SL8lza7P2W1Q1LvQJK/XnxXu9Vror/U
KVmSGfOnv6LttIWw7qw/lrhitxa+wL/HHLW/DjOuvwyODtXqfKm/gKJ3g9Ka
QD9VYDa00R60v7aisqgYi6O/BjLVNBpSiL9Jk2qsRJyZv+krqeGmnbS/OyVk
vw==
"], {
{Hue[0, 1, 0.56], Arrowheads[0.04999376097487097], Arrow3DBox[TubeBox[{1, 8}], 0.008175273356231982], Arrow3DBox[TubeBox[{1, 11}], 0.008175273356231982], Arrow3DBox[TubeBox[{1, 16}], 0.008175273356231982], Arrow3DBox[TubeBox[{2, 4}], 0.008175273356231982], Arrow3DBox[TubeBox[{2, 9}], 0.008175273356231982], Arrow3DBox[TubeBox[{2, 14}], 0.008175273356231982], Arrow3DBox[TubeBox[{2, 17}], 0.008175273356231982], Arrow3DBox[TubeBox[{2, 19}], 0.008175273356231982], Arrow3DBox[TubeBox[{2, 21}], 0.008175273356231982], Arrow3DBox[TubeBox[{2, 26}], 0.008175273356231982], Arrow3DBox[TubeBox[{7, 11}], 0.008175273356231982], Arrow3DBox[TubeBox[{10, 8}], 0.008175273356231982], Arrow3DBox[TubeBox[{12, 8}], 0.008175273356231982], Arrow3DBox[TubeBox[{13, 4}], 0.008175273356231982], Arrow3DBox[TubeBox[{13, 17}], 0.008175273356231982], Arrow3DBox[TubeBox[{13, 19}], 0.008175273356231982], Arrow3DBox[TubeBox[{13, 21}], 0.008175273356231982], Arrow3DBox[TubeBox[{13, 26}], 0.008175273356231982], Arrow3DBox[TubeBox[{17, 1}], 0.008175273356231982], Arrow3DBox[TubeBox[{17, 7}], 0.008175273356231982], Arrow3DBox[TubeBox[{17, 27}], 0.008175273356231982], Arrow3DBox[TubeBox[{18, 4}], 0.008175273356231982], Arrow3DBox[TubeBox[{18, 19}], 0.008175273356231982], Arrow3DBox[TubeBox[{20, 22}], 0.008175273356231982], Arrow3DBox[TubeBox[{20, 24}], 0.008175273356231982], Arrow3DBox[TubeBox[{21, 8}], 0.008175273356231982], Arrow3DBox[TubeBox[{21, 15}], 0.008175273356231982], Arrow3DBox[TubeBox[{21, 16}], 0.008175273356231982], Arrow3DBox[TubeBox[{22, 4}], 0.008175273356231982], Arrow3DBox[TubeBox[{22, 14}], 0.008175273356231982], Arrow3DBox[TubeBox[{22, 17}], 0.008175273356231982], Arrow3DBox[TubeBox[{22, 19}], 0.008175273356231982], Arrow3DBox[TubeBox[{22, 21}], 0.008175273356231982], Arrow3DBox[TubeBox[{22, 26}], 0.008175273356231982], Arrow3DBox[TubeBox[{24, 3}], 0.008175273356231982], Arrow3DBox[TubeBox[{24, 4}], 0.008175273356231982], Arrow3DBox[TubeBox[{24, 5}], 0.008175273356231982], Arrow3DBox[TubeBox[{24, 6}], 0.008175273356231982], Arrow3DBox[TubeBox[{24, 9}], 0.008175273356231982], Arrow3DBox[TubeBox[{24, 17}], 0.008175273356231982], Arrow3DBox[TubeBox[{24, 19}], 0.008175273356231982], Arrow3DBox[TubeBox[{24, 21}], 0.008175273356231982], Arrow3DBox[TubeBox[{24, 25}], 0.008175273356231982], Arrow3DBox[TubeBox[{24, 26}], 0.008175273356231982], Arrow3DBox[TubeBox[{25, 14}], 0.008175273356231982], Arrow3DBox[TubeBox[{26, 1}], 0.008175273356231982], Arrow3DBox[TubeBox[{26, 7}], 0.008175273356231982], Arrow3DBox[TubeBox[{26, 15}], 0.008175273356231982], Arrow3DBox[TubeBox[{27, 8}], 0.008175273356231982], Arrow3DBox[TubeBox[{27, 16}], 0.008175273356231982]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], SphereBox[1, 0.008175273356231982], SphereBox[2, 0.008175273356231982], SphereBox[3, 0.008175273356231982], SphereBox[4, 0.008175273356231982], SphereBox[5, 0.008175273356231982], SphereBox[6, 0.008175273356231982], SphereBox[7, 0.008175273356231982], SphereBox[8, 0.008175273356231982], SphereBox[9, 0.008175273356231982], SphereBox[10, 0.008175273356231982], SphereBox[11, 0.008175273356231982], SphereBox[12, 0.008175273356231982], SphereBox[13, 0.008175273356231982], SphereBox[14, 0.008175273356231982], SphereBox[15, 0.008175273356231982], SphereBox[16, 0.008175273356231982], SphereBox[17, 0.008175273356231982], SphereBox[18, 0.008175273356231982], SphereBox[19, 0.008175273356231982], SphereBox[20, 0.008175273356231982], SphereBox[21, 0.008175273356231982], SphereBox[22, 0.008175273356231982], SphereBox[23, 0.008175273356231982], SphereBox[24, 0.008175273356231982], SphereBox[25, 0.008175273356231982], SphereBox[26, 0.008175273356231982], SphereBox[27, 0.008175273356231982]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
Boxed->False,
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}}]\), 3]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/4c046cca2b33be2f.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/c75dc1c2-a612-4820-a760-2572505e9948"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/374f6b6387496c61.png)
![ResourceFunction["CausalGraphEntanglementEntropyNaive"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
SparseArray[Automatic, {100, 100}, 0, {1, {CompressedData["
1:eJwt0L8rxHEAgOGvcuVX3XAldadOyXAKUVcuXZSSRblFyaWIwXAki5LSTTdY
LDZdBlcWk4nFIFJSyiLdIIPFwKYbeOo+bz3/wNu3slkotURRtBY1i9FOJ3ES
dJMkzQAZBhlmlGyQY4I8k0wzwyxzzLPAIksUWWaVdTYoBVtss8Mue+xzQJkK
hxxxzAlVTjmjxjkXwSVXXHPDLXfBPQ888sQzL8Erb9R554NPvvjmh18a/NFq
ZhsddBEnQQ8peknTT4YhRhgjyzg58kzxD6YDLiw=
"], CompressedData["
1:eJwdj1lTglAAhXFJ3MEIRiVATMRMGzavIoLhQuJUNOCGjGLqe///LXLmPH5n
Y8+/7jkOQZAZg6BIUJJ4elvRdY4nRjhpeUXq4yuerCQbrfaqSDFaUGT6mu2l
0Mf1N6sMJplmoIw31zon+vz4VUXURKPl8bMQ6PlCubOLdaUoy3JDRPWFkYGo
D87xFPFwzrBpzQzSfYIkjoKyuVwF0SFIzPjBrSxTe17uUujAhBlFCwRx5oRF
psn3+nvgAx0uVe0qJoObixJEJYor0Zztzm5kCa9aol+/H6YzF8llpq6kBXA2
N9wiPL1l5cG0Pf5vL5TNySn/0p0famxnOn9fAj+FtlexQlfqNfiWJ4jkJyca
mOyECZR8XMcri42uXK5R+eEG7fGR5QEdAX70ONdZ3GGUDKJZf1lFQCA=
"]}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.032577280450710414`], ArrowBox[CompressedData["
1:eJwVxVmbqQAAAFDZkiUZa4ySQbaotJF9G2FCkSXE1Pv8/7f73fNyiN8/7dft
crkmgMv1f8ALpIAvYAwc3Zi76C67SU/K0/cmvTnv0qv7YF/et/Wpfrff60dB
L1gCq2AdPAbgQD6AB+SACcEQDomQDCmQHvQHkeBn8BTah4kwF5bC0wgUqURM
mINHsAE7SBEpIwxyjZGx0UfroxuPxrsJT6KUqCb0JJmcJ62UkBqkw+lIOpNu
pi8ZIENlWBRDi2gZXaIaamWj2W72mqNz/c9hPprvYglshz2xFz7CDdwpgIVQ
YVhQCIyQiQlhfgW+xFKqlCunys8KXeEqRsWuOCRNMuSumqrmavHasPauJ+vL
RrCBNwqNWmPduDT9TaQpNScUSOEUR8mU2aJbTGve2rWsNtzG25U22ebbYvtG
C/SVEZgBC7IxNssqnSwX5zqcwNM8xxu8zTtiXqRFRuREQ3QkUIpJmFSWFEnr
znt0j+nNe7ueJcfkpJyVl32mfx0WRx+j3jgwhsb2hJ1oU3w6m2ozdibPzAW4
CC5Ci97ivIwuyW/s+7wiVp2VtJopdWW0Bteh9XCtbCKbzGaymW5e2/C2saW2
i5+HWlAJtanO1IX6ra53wu669++RfX1/PACHyIE6sAdeK2mkVtV0ndaZY+74
cyqfmNPQiBsdY2dYZ88ZOefOn+fTxX1BL6uLcR3cuJt9c8yYmTUV83EH7pE7
dWfv/P32SD76j+VDfwrPgRW1BOv6Kr2qL/0dejffq1+fHbfzdscWnLjTcYR/
cYJ+xw==
"], 0.007682766082629425]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.007682766082629425], DiskBox[2, 0.007682766082629425], DiskBox[3, 0.007682766082629425], DiskBox[4, 0.007682766082629425], DiskBox[5, 0.007682766082629425], DiskBox[6, 0.007682766082629425], DiskBox[7, 0.007682766082629425], DiskBox[8, 0.007682766082629425], DiskBox[9, 0.007682766082629425], DiskBox[10, 0.007682766082629425], DiskBox[11, 0.007682766082629425], DiskBox[12, 0.007682766082629425], DiskBox[13, 0.007682766082629425], DiskBox[14, 0.007682766082629425], DiskBox[15, 0.007682766082629425], DiskBox[16, 0.007682766082629425], DiskBox[17, 0.007682766082629425], DiskBox[18, 0.007682766082629425], DiskBox[19, 0.007682766082629425], DiskBox[20, 0.007682766082629425], DiskBox[21, 0.007682766082629425], DiskBox[22, 0.007682766082629425], DiskBox[23, 0.007682766082629425], DiskBox[24, 0.007682766082629425], DiskBox[25, 0.007682766082629425], DiskBox[26, 0.007682766082629425], DiskBox[27, 0.007682766082629425], DiskBox[28, 0.007682766082629425], DiskBox[29, 0.007682766082629425], DiskBox[30, 0.007682766082629425], DiskBox[31, 0.007682766082629425], DiskBox[32, 0.007682766082629425], DiskBox[33, 0.007682766082629425], DiskBox[34, 0.007682766082629425], DiskBox[35, 0.007682766082629425], DiskBox[36, 0.007682766082629425], DiskBox[37, 0.007682766082629425], DiskBox[38, 0.007682766082629425], DiskBox[39, 0.007682766082629425], DiskBox[40, 0.007682766082629425], DiskBox[41, 0.007682766082629425], DiskBox[42, 0.007682766082629425], DiskBox[43, 0.007682766082629425], DiskBox[44, 0.007682766082629425], DiskBox[45, 0.007682766082629425], DiskBox[46, 0.007682766082629425], DiskBox[47, 0.007682766082629425], DiskBox[48, 0.007682766082629425], DiskBox[49, 0.007682766082629425], DiskBox[50, 0.007682766082629425], DiskBox[51, 0.007682766082629425], DiskBox[52, 0.007682766082629425], DiskBox[53, 0.007682766082629425], DiskBox[54, 0.007682766082629425], DiskBox[55, 0.007682766082629425], DiskBox[56, 0.007682766082629425], DiskBox[57, 0.007682766082629425], DiskBox[58, 0.007682766082629425], DiskBox[59, 0.007682766082629425], DiskBox[60, 0.007682766082629425], DiskBox[61, 0.007682766082629425], DiskBox[62, 0.007682766082629425], DiskBox[63, 0.007682766082629425], DiskBox[64, 0.007682766082629425], DiskBox[65, 0.007682766082629425], DiskBox[66, 0.007682766082629425], DiskBox[67, 0.007682766082629425], DiskBox[68, 0.007682766082629425], DiskBox[69, 0.007682766082629425], DiskBox[70, 0.007682766082629425], DiskBox[71, 0.007682766082629425], DiskBox[72, 0.007682766082629425], DiskBox[73, 0.007682766082629425], DiskBox[74, 0.007682766082629425], DiskBox[75, 0.007682766082629425], DiskBox[76, 0.007682766082629425], DiskBox[77, 0.007682766082629425], DiskBox[78, 0.007682766082629425], DiskBox[79, 0.007682766082629425], DiskBox[80, 0.007682766082629425], DiskBox[81, 0.007682766082629425], DiskBox[82, 0.007682766082629425], DiskBox[83, 0.007682766082629425], DiskBox[84, 0.007682766082629425], DiskBox[85, 0.007682766082629425], DiskBox[86, 0.007682766082629425], DiskBox[87, 0.007682766082629425], DiskBox[88, 0.007682766082629425], DiskBox[89, 0.007682766082629425], DiskBox[90, 0.007682766082629425], DiskBox[91, 0.007682766082629425], DiskBox[92, 0.007682766082629425], DiskBox[93, 0.007682766082629425], DiskBox[94, 0.007682766082629425], DiskBox[95, 0.007682766082629425], DiskBox[96, 0.007682766082629425], DiskBox[97, 0.007682766082629425], DiskBox[98, 0.007682766082629425], DiskBox[99, 0.007682766082629425], DiskBox[100, 0.007682766082629425]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
SparseArray[
Automatic, {23, 23}, 0, {1, {{0, 2, 5, 6, 7, 7, 10, 12, 12, 15, 19, 19, 22, 24, 26, 29, 29, 32, 34, 35, 35, 36, 39, 41}, {{5}, {16}, {
1}, {7}, {21}, {13}, {8}, {12}, {14}, {22}, {5}, {16}, {
2}, {3}, {18}, {2}, {3}, {18}, {20}, {3}, {5}, {16}, {
4}, {11}, {9}, {20}, {9}, {12}, {22}, {6}, {10}, {15}, {
7}, {13}, {23}, {19}, {3}, {18}, {23}, {5}, {16}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.04146110156920305], ArrowBox[{1, 5}, 0.0036549079020560286`], ArrowBox[{1, 16}, 0.0036549079020560286`], ArrowBox[{2, 1}, 0.0036549079020560286`], ArrowBox[{2, 7}, 0.0036549079020560286`], ArrowBox[{2, 21}, 0.0036549079020560286`], ArrowBox[{3, 13}, 0.0036549079020560286`], ArrowBox[{4, 8}, 0.0036549079020560286`], ArrowBox[{6, 12}, 0.0036549079020560286`], ArrowBox[{6, 14}, 0.0036549079020560286`], ArrowBox[{6, 22}, 0.0036549079020560286`], ArrowBox[{7, 5}, 0.0036549079020560286`], ArrowBox[{7, 16}, 0.0036549079020560286`], ArrowBox[{9, 2}, 0.0036549079020560286`], ArrowBox[{9, 3}, 0.0036549079020560286`], ArrowBox[{9, 18}, 0.0036549079020560286`], ArrowBox[{10, 2}, 0.0036549079020560286`], ArrowBox[{10, 3}, 0.0036549079020560286`], ArrowBox[{10, 18}, 0.0036549079020560286`], ArrowBox[{10, 20}, 0.0036549079020560286`], ArrowBox[{12, 3}, 0.0036549079020560286`], ArrowBox[{12, 5}, 0.0036549079020560286`], ArrowBox[{12, 16}, 0.0036549079020560286`], ArrowBox[{13, 4}, 0.0036549079020560286`], ArrowBox[{13, 11}, 0.0036549079020560286`], ArrowBox[{14, 9}, 0.0036549079020560286`], ArrowBox[{14, 20}, 0.0036549079020560286`], ArrowBox[{15, 9}, 0.0036549079020560286`], ArrowBox[{15, 12}, 0.0036549079020560286`], ArrowBox[{15, 22}, 0.0036549079020560286`], ArrowBox[{17, 6}, 0.0036549079020560286`], ArrowBox[{17, 10}, 0.0036549079020560286`], ArrowBox[{17, 15}, 0.0036549079020560286`], ArrowBox[{18, 7}, 0.0036549079020560286`], ArrowBox[{18, 13}, 0.0036549079020560286`], ArrowBox[{19, 23}, 0.0036549079020560286`], ArrowBox[{21, 19}, 0.0036549079020560286`], ArrowBox[{22, 3}, 0.0036549079020560286`], ArrowBox[{22, 18}, 0.0036549079020560286`], ArrowBox[{22, 23}, 0.0036549079020560286`], ArrowBox[{23, 5}, 0.0036549079020560286`], ArrowBox[{23, 16}, 0.0036549079020560286`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.0036549079020560286], DiskBox[2, 0.0036549079020560286], DiskBox[3, 0.0036549079020560286], DiskBox[4, 0.0036549079020560286], DiskBox[5, 0.0036549079020560286], DiskBox[6, 0.0036549079020560286], DiskBox[7, 0.0036549079020560286], DiskBox[8, 0.0036549079020560286], DiskBox[9, 0.0036549079020560286], DiskBox[10, 0.0036549079020560286], DiskBox[11, 0.0036549079020560286], DiskBox[12, 0.0036549079020560286], DiskBox[13, 0.0036549079020560286], DiskBox[14, 0.0036549079020560286], DiskBox[15, 0.0036549079020560286], DiskBox[16, 0.0036549079020560286], DiskBox[17, 0.0036549079020560286], DiskBox[18, 0.0036549079020560286], DiskBox[19, 0.0036549079020560286], DiskBox[20, 0.0036549079020560286], DiskBox[21, 0.0036549079020560286], DiskBox[22, 0.0036549079020560286], DiskBox[23, 0.0036549079020560286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), 2, "EntanglementEntropy"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/4a76fb5a9d513a80.png)
![ResourceFunction["CausalGraphEntanglementEntropyNaive"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
SparseArray[Automatic, {100, 100}, 0, {1, {CompressedData["
1:eJwt0L8rxHEAgOGvcuVX3XAldadOyXAKUVcuXZSSRblFyaWIwXAki5LSTTdY
LDZdBlcWk4nFIFJSyiLdIIPFwKYbeOo+bz3/wNu3slkotURRtBY1i9FOJ3ES
dJMkzQAZBhlmlGyQY4I8k0wzwyxzzLPAIksUWWaVdTYoBVtss8Mue+xzQJkK
hxxxzAlVTjmjxjkXwSVXXHPDLXfBPQ888sQzL8Erb9R554NPvvjmh18a/NFq
ZhsddBEnQQ8peknTT4YhRhgjyzg58kzxD6YDLiw=
"], CompressedData["
1:eJwdj1lTglAAhXFJ3MEIRiVATMRMGzavIoLhQuJUNOCGjGLqe///LXLmPH5n
Y8+/7jkOQZAZg6BIUJJ4elvRdY4nRjhpeUXq4yuerCQbrfaqSDFaUGT6mu2l
0Mf1N6sMJplmoIw31zon+vz4VUXURKPl8bMQ6PlCubOLdaUoy3JDRPWFkYGo
D87xFPFwzrBpzQzSfYIkjoKyuVwF0SFIzPjBrSxTe17uUujAhBlFCwRx5oRF
psn3+nvgAx0uVe0qJoObixJEJYor0Zztzm5kCa9aol+/H6YzF8llpq6kBXA2
N9wiPL1l5cG0Pf5vL5TNySn/0p0famxnOn9fAj+FtlexQlfqNfiWJ4jkJyca
mOyECZR8XMcri42uXK5R+eEG7fGR5QEdAX70ONdZ3GGUDKJZf1lFQCA=
"]}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.032577280450710414`], ArrowBox[CompressedData["
1:eJwVxVmbqQAAAFDZkiUZa4ySQbaotJF9G2FCkSXE1Pv8/7f73fNyiN8/7dft
crkmgMv1f8ALpIAvYAwc3Zi76C67SU/K0/cmvTnv0qv7YF/et/Wpfrff60dB
L1gCq2AdPAbgQD6AB+SACcEQDomQDCmQHvQHkeBn8BTah4kwF5bC0wgUqURM
mINHsAE7SBEpIwxyjZGx0UfroxuPxrsJT6KUqCb0JJmcJ62UkBqkw+lIOpNu
pi8ZIENlWBRDi2gZXaIaamWj2W72mqNz/c9hPprvYglshz2xFz7CDdwpgIVQ
YVhQCIyQiQlhfgW+xFKqlCunys8KXeEqRsWuOCRNMuSumqrmavHasPauJ+vL
RrCBNwqNWmPduDT9TaQpNScUSOEUR8mU2aJbTGve2rWsNtzG25U22ebbYvtG
C/SVEZgBC7IxNssqnSwX5zqcwNM8xxu8zTtiXqRFRuREQ3QkUIpJmFSWFEnr
znt0j+nNe7ueJcfkpJyVl32mfx0WRx+j3jgwhsb2hJ1oU3w6m2ozdibPzAW4
CC5Ci97ivIwuyW/s+7wiVp2VtJopdWW0Bteh9XCtbCKbzGaymW5e2/C2saW2
i5+HWlAJtanO1IX6ra53wu669++RfX1/PACHyIE6sAdeK2mkVtV0ndaZY+74
cyqfmNPQiBsdY2dYZ88ZOefOn+fTxX1BL6uLcR3cuJt9c8yYmTUV83EH7pE7
dWfv/P32SD76j+VDfwrPgRW1BOv6Kr2qL/0dejffq1+fHbfzdscWnLjTcYR/
cYJ+xw==
"], 0.007682766082629425]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.007682766082629425], DiskBox[2, 0.007682766082629425], DiskBox[3, 0.007682766082629425], DiskBox[4, 0.007682766082629425], DiskBox[5, 0.007682766082629425], DiskBox[6, 0.007682766082629425], DiskBox[7, 0.007682766082629425], DiskBox[8, 0.007682766082629425], DiskBox[9, 0.007682766082629425], DiskBox[10, 0.007682766082629425], DiskBox[11, 0.007682766082629425], DiskBox[12, 0.007682766082629425], DiskBox[13, 0.007682766082629425], DiskBox[14, 0.007682766082629425], DiskBox[15, 0.007682766082629425], DiskBox[16, 0.007682766082629425], DiskBox[17, 0.007682766082629425], DiskBox[18, 0.007682766082629425], DiskBox[19, 0.007682766082629425], DiskBox[20, 0.007682766082629425], DiskBox[21, 0.007682766082629425], DiskBox[22, 0.007682766082629425], DiskBox[23, 0.007682766082629425], DiskBox[24, 0.007682766082629425], DiskBox[25, 0.007682766082629425], DiskBox[26, 0.007682766082629425], DiskBox[27, 0.007682766082629425], DiskBox[28, 0.007682766082629425], DiskBox[29, 0.007682766082629425], DiskBox[30, 0.007682766082629425], DiskBox[31, 0.007682766082629425], DiskBox[32, 0.007682766082629425], DiskBox[33, 0.007682766082629425], DiskBox[34, 0.007682766082629425], DiskBox[35, 0.007682766082629425], DiskBox[36, 0.007682766082629425], DiskBox[37, 0.007682766082629425], DiskBox[38, 0.007682766082629425], DiskBox[39, 0.007682766082629425], DiskBox[40, 0.007682766082629425], DiskBox[41, 0.007682766082629425], DiskBox[42, 0.007682766082629425], DiskBox[43, 0.007682766082629425], DiskBox[44, 0.007682766082629425], DiskBox[45, 0.007682766082629425], DiskBox[46, 0.007682766082629425], DiskBox[47, 0.007682766082629425], DiskBox[48, 0.007682766082629425], DiskBox[49, 0.007682766082629425], DiskBox[50, 0.007682766082629425], DiskBox[51, 0.007682766082629425], DiskBox[52, 0.007682766082629425], DiskBox[53, 0.007682766082629425], DiskBox[54, 0.007682766082629425], DiskBox[55, 0.007682766082629425], DiskBox[56, 0.007682766082629425], DiskBox[57, 0.007682766082629425], DiskBox[58, 0.007682766082629425], DiskBox[59, 0.007682766082629425], DiskBox[60, 0.007682766082629425], DiskBox[61, 0.007682766082629425], DiskBox[62, 0.007682766082629425], DiskBox[63, 0.007682766082629425], DiskBox[64, 0.007682766082629425], DiskBox[65, 0.007682766082629425], DiskBox[66, 0.007682766082629425], DiskBox[67, 0.007682766082629425], DiskBox[68, 0.007682766082629425], DiskBox[69, 0.007682766082629425], DiskBox[70, 0.007682766082629425], DiskBox[71, 0.007682766082629425], DiskBox[72, 0.007682766082629425], DiskBox[73, 0.007682766082629425], DiskBox[74, 0.007682766082629425], DiskBox[75, 0.007682766082629425], DiskBox[76, 0.007682766082629425], DiskBox[77, 0.007682766082629425], DiskBox[78, 0.007682766082629425], DiskBox[79, 0.007682766082629425], DiskBox[80, 0.007682766082629425], DiskBox[81, 0.007682766082629425], DiskBox[82, 0.007682766082629425], DiskBox[83, 0.007682766082629425], DiskBox[84, 0.007682766082629425], DiskBox[85, 0.007682766082629425], DiskBox[86, 0.007682766082629425], DiskBox[87, 0.007682766082629425], DiskBox[88, 0.007682766082629425], DiskBox[89, 0.007682766082629425], DiskBox[90, 0.007682766082629425], DiskBox[91, 0.007682766082629425], DiskBox[92, 0.007682766082629425], DiskBox[93, 0.007682766082629425], DiskBox[94, 0.007682766082629425], DiskBox[95, 0.007682766082629425], DiskBox[96, 0.007682766082629425], DiskBox[97, 0.007682766082629425], DiskBox[98, 0.007682766082629425], DiskBox[99, 0.007682766082629425], DiskBox[100, 0.007682766082629425]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
SparseArray[
Automatic, {23, 23}, 0, {1, {{0, 2, 5, 6, 7, 7, 10, 12, 12, 15, 19, 19, 22, 24, 26, 29, 29, 32, 34, 35, 35, 36, 39, 41}, {{5}, {16}, {
1}, {7}, {21}, {13}, {8}, {12}, {14}, {22}, {5}, {16}, {
2}, {3}, {18}, {2}, {3}, {18}, {20}, {3}, {5}, {16}, {
4}, {11}, {9}, {20}, {9}, {12}, {22}, {6}, {10}, {15}, {
7}, {13}, {23}, {19}, {3}, {18}, {23}, {5}, {16}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.04146110156920305], ArrowBox[{1, 5}, 0.0036549079020560286`], ArrowBox[{1, 16}, 0.0036549079020560286`], ArrowBox[{2, 1}, 0.0036549079020560286`], ArrowBox[{2, 7}, 0.0036549079020560286`], ArrowBox[{2, 21}, 0.0036549079020560286`], ArrowBox[{3, 13}, 0.0036549079020560286`], ArrowBox[{4, 8}, 0.0036549079020560286`], ArrowBox[{6, 12}, 0.0036549079020560286`], ArrowBox[{6, 14}, 0.0036549079020560286`], ArrowBox[{6, 22}, 0.0036549079020560286`], ArrowBox[{7, 5}, 0.0036549079020560286`], ArrowBox[{7, 16}, 0.0036549079020560286`], ArrowBox[{9, 2}, 0.0036549079020560286`], ArrowBox[{9, 3}, 0.0036549079020560286`], ArrowBox[{9, 18}, 0.0036549079020560286`], ArrowBox[{10, 2}, 0.0036549079020560286`], ArrowBox[{10, 3}, 0.0036549079020560286`], ArrowBox[{10, 18}, 0.0036549079020560286`], ArrowBox[{10, 20}, 0.0036549079020560286`], ArrowBox[{12, 3}, 0.0036549079020560286`], ArrowBox[{12, 5}, 0.0036549079020560286`], ArrowBox[{12, 16}, 0.0036549079020560286`], ArrowBox[{13, 4}, 0.0036549079020560286`], ArrowBox[{13, 11}, 0.0036549079020560286`], ArrowBox[{14, 9}, 0.0036549079020560286`], ArrowBox[{14, 20}, 0.0036549079020560286`], ArrowBox[{15, 9}, 0.0036549079020560286`], ArrowBox[{15, 12}, 0.0036549079020560286`], ArrowBox[{15, 22}, 0.0036549079020560286`], ArrowBox[{17, 6}, 0.0036549079020560286`], ArrowBox[{17, 10}, 0.0036549079020560286`], ArrowBox[{17, 15}, 0.0036549079020560286`], ArrowBox[{18, 7}, 0.0036549079020560286`], ArrowBox[{18, 13}, 0.0036549079020560286`], ArrowBox[{19, 23}, 0.0036549079020560286`], ArrowBox[{21, 19}, 0.0036549079020560286`], ArrowBox[{22, 3}, 0.0036549079020560286`], ArrowBox[{22, 18}, 0.0036549079020560286`], ArrowBox[{22, 23}, 0.0036549079020560286`], ArrowBox[{23, 5}, 0.0036549079020560286`], ArrowBox[{23, 16}, 0.0036549079020560286`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.0036549079020560286], DiskBox[2, 0.0036549079020560286], DiskBox[3, 0.0036549079020560286], DiskBox[4, 0.0036549079020560286], DiskBox[5, 0.0036549079020560286], DiskBox[6, 0.0036549079020560286], DiskBox[7, 0.0036549079020560286], DiskBox[8, 0.0036549079020560286], DiskBox[9, 0.0036549079020560286], DiskBox[10, 0.0036549079020560286], DiskBox[11, 0.0036549079020560286], DiskBox[12, 0.0036549079020560286], DiskBox[13, 0.0036549079020560286], DiskBox[14, 0.0036549079020560286], DiskBox[15, 0.0036549079020560286], DiskBox[16, 0.0036549079020560286], DiskBox[17, 0.0036549079020560286], DiskBox[18, 0.0036549079020560286], DiskBox[19, 0.0036549079020560286], DiskBox[20, 0.0036549079020560286], DiskBox[21, 0.0036549079020560286], DiskBox[22, 0.0036549079020560286], DiskBox[23, 0.0036549079020560286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), 2, "CausalGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/1c59dfdaaa9518c4.png)
![ResourceFunction["CausalGraphEntanglementEntropyNaive"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
SparseArray[Automatic, {100, 100}, 0, {1, {CompressedData["
1:eJwt0L8rxHEAgOGvcuVX3XAldadOyXAKUVcuXZSSRblFyaWIwXAki5LSTTdY
LDZdBlcWk4nFIFJSyiLdIIPFwKYbeOo+bz3/wNu3slkotURRtBY1i9FOJ3ES
dJMkzQAZBhlmlGyQY4I8k0wzwyxzzLPAIksUWWaVdTYoBVtss8Mue+xzQJkK
hxxxzAlVTjmjxjkXwSVXXHPDLXfBPQ888sQzL8Erb9R554NPvvjmh18a/NFq
ZhsddBEnQQ8peknTT4YhRhgjyzg58kzxD6YDLiw=
"], CompressedData["
1:eJwdj1lTglAAhXFJ3MEIRiVATMRMGzavIoLhQuJUNOCGjGLqe///LXLmPH5n
Y8+/7jkOQZAZg6BIUJJ4elvRdY4nRjhpeUXq4yuerCQbrfaqSDFaUGT6mu2l
0Mf1N6sMJplmoIw31zon+vz4VUXURKPl8bMQ6PlCubOLdaUoy3JDRPWFkYGo
D87xFPFwzrBpzQzSfYIkjoKyuVwF0SFIzPjBrSxTe17uUujAhBlFCwRx5oRF
psn3+nvgAx0uVe0qJoObixJEJYor0Zztzm5kCa9aol+/H6YzF8llpq6kBXA2
N9wiPL1l5cG0Pf5vL5TNySn/0p0famxnOn9fAj+FtlexQlfqNfiWJ4jkJyca
mOyECZR8XMcri42uXK5R+eEG7fGR5QEdAX70ONdZ3GGUDKJZf1lFQCA=
"]}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.032577280450710414`], ArrowBox[CompressedData["
1:eJwVxVmbqQAAAFDZkiUZa4ySQbaotJF9G2FCkSXE1Pv8/7f73fNyiN8/7dft
crkmgMv1f8ALpIAvYAwc3Zi76C67SU/K0/cmvTnv0qv7YF/et/Wpfrff60dB
L1gCq2AdPAbgQD6AB+SACcEQDomQDCmQHvQHkeBn8BTah4kwF5bC0wgUqURM
mINHsAE7SBEpIwxyjZGx0UfroxuPxrsJT6KUqCb0JJmcJ62UkBqkw+lIOpNu
pi8ZIENlWBRDi2gZXaIaamWj2W72mqNz/c9hPprvYglshz2xFz7CDdwpgIVQ
YVhQCIyQiQlhfgW+xFKqlCunys8KXeEqRsWuOCRNMuSumqrmavHasPauJ+vL
RrCBNwqNWmPduDT9TaQpNScUSOEUR8mU2aJbTGve2rWsNtzG25U22ebbYvtG
C/SVEZgBC7IxNssqnSwX5zqcwNM8xxu8zTtiXqRFRuREQ3QkUIpJmFSWFEnr
znt0j+nNe7ueJcfkpJyVl32mfx0WRx+j3jgwhsb2hJ1oU3w6m2ozdibPzAW4
CC5Ci97ivIwuyW/s+7wiVp2VtJopdWW0Bteh9XCtbCKbzGaymW5e2/C2saW2
i5+HWlAJtanO1IX6ra53wu669++RfX1/PACHyIE6sAdeK2mkVtV0ndaZY+74
cyqfmNPQiBsdY2dYZ88ZOefOn+fTxX1BL6uLcR3cuJt9c8yYmTUV83EH7pE7
dWfv/P32SD76j+VDfwrPgRW1BOv6Kr2qL/0dejffq1+fHbfzdscWnLjTcYR/
cYJ+xw==
"], 0.007682766082629425]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.007682766082629425], DiskBox[2, 0.007682766082629425], DiskBox[3, 0.007682766082629425], DiskBox[4, 0.007682766082629425], DiskBox[5, 0.007682766082629425], DiskBox[6, 0.007682766082629425], DiskBox[7, 0.007682766082629425], DiskBox[8, 0.007682766082629425], DiskBox[9, 0.007682766082629425], DiskBox[10, 0.007682766082629425], DiskBox[11, 0.007682766082629425], DiskBox[12, 0.007682766082629425], DiskBox[13, 0.007682766082629425], DiskBox[14, 0.007682766082629425], DiskBox[15, 0.007682766082629425], DiskBox[16, 0.007682766082629425], DiskBox[17, 0.007682766082629425], DiskBox[18, 0.007682766082629425], DiskBox[19, 0.007682766082629425], DiskBox[20, 0.007682766082629425], DiskBox[21, 0.007682766082629425], DiskBox[22, 0.007682766082629425], DiskBox[23, 0.007682766082629425], DiskBox[24, 0.007682766082629425], DiskBox[25, 0.007682766082629425], DiskBox[26, 0.007682766082629425], DiskBox[27, 0.007682766082629425], DiskBox[28, 0.007682766082629425], DiskBox[29, 0.007682766082629425], DiskBox[30, 0.007682766082629425], DiskBox[31, 0.007682766082629425], DiskBox[32, 0.007682766082629425], DiskBox[33, 0.007682766082629425], DiskBox[34, 0.007682766082629425], DiskBox[35, 0.007682766082629425], DiskBox[36, 0.007682766082629425], DiskBox[37, 0.007682766082629425], DiskBox[38, 0.007682766082629425], DiskBox[39, 0.007682766082629425], DiskBox[40, 0.007682766082629425], DiskBox[41, 0.007682766082629425], DiskBox[42, 0.007682766082629425], DiskBox[43, 0.007682766082629425], DiskBox[44, 0.007682766082629425], DiskBox[45, 0.007682766082629425], DiskBox[46, 0.007682766082629425], DiskBox[47, 0.007682766082629425], DiskBox[48, 0.007682766082629425], DiskBox[49, 0.007682766082629425], DiskBox[50, 0.007682766082629425], DiskBox[51, 0.007682766082629425], DiskBox[52, 0.007682766082629425], DiskBox[53, 0.007682766082629425], DiskBox[54, 0.007682766082629425], DiskBox[55, 0.007682766082629425], DiskBox[56, 0.007682766082629425], DiskBox[57, 0.007682766082629425], DiskBox[58, 0.007682766082629425], DiskBox[59, 0.007682766082629425], DiskBox[60, 0.007682766082629425], DiskBox[61, 0.007682766082629425], DiskBox[62, 0.007682766082629425], DiskBox[63, 0.007682766082629425], DiskBox[64, 0.007682766082629425], DiskBox[65, 0.007682766082629425], DiskBox[66, 0.007682766082629425], DiskBox[67, 0.007682766082629425], DiskBox[68, 0.007682766082629425], DiskBox[69, 0.007682766082629425], DiskBox[70, 0.007682766082629425], DiskBox[71, 0.007682766082629425], DiskBox[72, 0.007682766082629425], DiskBox[73, 0.007682766082629425], DiskBox[74, 0.007682766082629425], DiskBox[75, 0.007682766082629425], DiskBox[76, 0.007682766082629425], DiskBox[77, 0.007682766082629425], DiskBox[78, 0.007682766082629425], DiskBox[79, 0.007682766082629425], DiskBox[80, 0.007682766082629425], DiskBox[81, 0.007682766082629425], DiskBox[82, 0.007682766082629425], DiskBox[83, 0.007682766082629425], DiskBox[84, 0.007682766082629425], DiskBox[85, 0.007682766082629425], DiskBox[86, 0.007682766082629425], DiskBox[87, 0.007682766082629425], DiskBox[88, 0.007682766082629425], DiskBox[89, 0.007682766082629425], DiskBox[90, 0.007682766082629425], DiskBox[91, 0.007682766082629425], DiskBox[92, 0.007682766082629425], DiskBox[93, 0.007682766082629425], DiskBox[94, 0.007682766082629425], DiskBox[95, 0.007682766082629425], DiskBox[96, 0.007682766082629425], DiskBox[97, 0.007682766082629425], DiskBox[98, 0.007682766082629425], DiskBox[99, 0.007682766082629425], DiskBox[100, 0.007682766082629425]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
SparseArray[
Automatic, {23, 23}, 0, {1, {{0, 2, 5, 6, 7, 7, 10, 12, 12, 15, 19, 19, 22, 24, 26, 29, 29, 32, 34, 35, 35, 36, 39, 41}, {{5}, {16}, {
1}, {7}, {21}, {13}, {8}, {12}, {14}, {22}, {5}, {16}, {
2}, {3}, {18}, {2}, {3}, {18}, {20}, {3}, {5}, {16}, {
4}, {11}, {9}, {20}, {9}, {12}, {22}, {6}, {10}, {15}, {
7}, {13}, {23}, {19}, {3}, {18}, {23}, {5}, {16}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.04146110156920305], ArrowBox[{1, 5}, 0.0036549079020560286`], ArrowBox[{1, 16}, 0.0036549079020560286`], ArrowBox[{2, 1}, 0.0036549079020560286`], ArrowBox[{2, 7}, 0.0036549079020560286`], ArrowBox[{2, 21}, 0.0036549079020560286`], ArrowBox[{3, 13}, 0.0036549079020560286`], ArrowBox[{4, 8}, 0.0036549079020560286`], ArrowBox[{6, 12}, 0.0036549079020560286`], ArrowBox[{6, 14}, 0.0036549079020560286`], ArrowBox[{6, 22}, 0.0036549079020560286`], ArrowBox[{7, 5}, 0.0036549079020560286`], ArrowBox[{7, 16}, 0.0036549079020560286`], ArrowBox[{9, 2}, 0.0036549079020560286`], ArrowBox[{9, 3}, 0.0036549079020560286`], ArrowBox[{9, 18}, 0.0036549079020560286`], ArrowBox[{10, 2}, 0.0036549079020560286`], ArrowBox[{10, 3}, 0.0036549079020560286`], ArrowBox[{10, 18}, 0.0036549079020560286`], ArrowBox[{10, 20}, 0.0036549079020560286`], ArrowBox[{12, 3}, 0.0036549079020560286`], ArrowBox[{12, 5}, 0.0036549079020560286`], ArrowBox[{12, 16}, 0.0036549079020560286`], ArrowBox[{13, 4}, 0.0036549079020560286`], ArrowBox[{13, 11}, 0.0036549079020560286`], ArrowBox[{14, 9}, 0.0036549079020560286`], ArrowBox[{14, 20}, 0.0036549079020560286`], ArrowBox[{15, 9}, 0.0036549079020560286`], ArrowBox[{15, 12}, 0.0036549079020560286`], ArrowBox[{15, 22}, 0.0036549079020560286`], ArrowBox[{17, 6}, 0.0036549079020560286`], ArrowBox[{17, 10}, 0.0036549079020560286`], ArrowBox[{17, 15}, 0.0036549079020560286`], ArrowBox[{18, 7}, 0.0036549079020560286`], ArrowBox[{18, 13}, 0.0036549079020560286`], ArrowBox[{19, 23}, 0.0036549079020560286`], ArrowBox[{21, 19}, 0.0036549079020560286`], ArrowBox[{22, 3}, 0.0036549079020560286`], ArrowBox[{22, 18}, 0.0036549079020560286`], ArrowBox[{22, 23}, 0.0036549079020560286`], ArrowBox[{23, 5}, 0.0036549079020560286`], ArrowBox[{23, 16}, 0.0036549079020560286`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.0036549079020560286], DiskBox[2, 0.0036549079020560286], DiskBox[3, 0.0036549079020560286], DiskBox[4, 0.0036549079020560286], DiskBox[5, 0.0036549079020560286], DiskBox[6, 0.0036549079020560286], DiskBox[7, 0.0036549079020560286], DiskBox[8, 0.0036549079020560286], DiskBox[9, 0.0036549079020560286], DiskBox[10, 0.0036549079020560286], DiskBox[11, 0.0036549079020560286], DiskBox[12, 0.0036549079020560286], DiskBox[13, 0.0036549079020560286], DiskBox[14, 0.0036549079020560286], DiskBox[15, 0.0036549079020560286], DiskBox[16, 0.0036549079020560286], DiskBox[17, 0.0036549079020560286], DiskBox[18, 0.0036549079020560286], DiskBox[19, 0.0036549079020560286], DiskBox[20, 0.0036549079020560286], DiskBox[21, 0.0036549079020560286], DiskBox[22, 0.0036549079020560286], DiskBox[23, 0.0036549079020560286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), 2, "FullCausalGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/2de5998391978abd.png)
![ResourceFunction["CausalGraphEntanglementEntropyNaive"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
SparseArray[Automatic, {100, 100}, 0, {1, {CompressedData["
1:eJwt0L8rxHEAgOGvcuVX3XAldadOyXAKUVcuXZSSRblFyaWIwXAki5LSTTdY
LDZdBlcWk4nFIFJSyiLdIIPFwKYbeOo+bz3/wNu3slkotURRtBY1i9FOJ3ES
dJMkzQAZBhlmlGyQY4I8k0wzwyxzzLPAIksUWWaVdTYoBVtss8Mue+xzQJkK
hxxxzAlVTjmjxjkXwSVXXHPDLXfBPQ888sQzL8Erb9R554NPvvjmh18a/NFq
ZhsddBEnQQ8peknTT4YhRhgjyzg58kzxD6YDLiw=
"], CompressedData["
1:eJwdj1lTglAAhXFJ3MEIRiVATMRMGzavIoLhQuJUNOCGjGLqe///LXLmPH5n
Y8+/7jkOQZAZg6BIUJJ4elvRdY4nRjhpeUXq4yuerCQbrfaqSDFaUGT6mu2l
0Mf1N6sMJplmoIw31zon+vz4VUXURKPl8bMQ6PlCubOLdaUoy3JDRPWFkYGo
D87xFPFwzrBpzQzSfYIkjoKyuVwF0SFIzPjBrSxTe17uUujAhBlFCwRx5oRF
psn3+nvgAx0uVe0qJoObixJEJYor0Zztzm5kCa9aol+/H6YzF8llpq6kBXA2
N9wiPL1l5cG0Pf5vL5TNySn/0p0famxnOn9fAj+FtlexQlfqNfiWJ4jkJyca
mOyECZR8XMcri42uXK5R+eEG7fGR5QEdAX70ONdZ3GGUDKJZf1lFQCA=
"]}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.032577280450710414`], ArrowBox[CompressedData["
1:eJwVxVmbqQAAAFDZkiUZa4ySQbaotJF9G2FCkSXE1Pv8/7f73fNyiN8/7dft
crkmgMv1f8ALpIAvYAwc3Zi76C67SU/K0/cmvTnv0qv7YF/et/Wpfrff60dB
L1gCq2AdPAbgQD6AB+SACcEQDomQDCmQHvQHkeBn8BTah4kwF5bC0wgUqURM
mINHsAE7SBEpIwxyjZGx0UfroxuPxrsJT6KUqCb0JJmcJ62UkBqkw+lIOpNu
pi8ZIENlWBRDi2gZXaIaamWj2W72mqNz/c9hPprvYglshz2xFz7CDdwpgIVQ
YVhQCIyQiQlhfgW+xFKqlCunys8KXeEqRsWuOCRNMuSumqrmavHasPauJ+vL
RrCBNwqNWmPduDT9TaQpNScUSOEUR8mU2aJbTGve2rWsNtzG25U22ebbYvtG
C/SVEZgBC7IxNssqnSwX5zqcwNM8xxu8zTtiXqRFRuREQ3QkUIpJmFSWFEnr
znt0j+nNe7ueJcfkpJyVl32mfx0WRx+j3jgwhsb2hJ1oU3w6m2ozdibPzAW4
CC5Ci97ivIwuyW/s+7wiVp2VtJopdWW0Bteh9XCtbCKbzGaymW5e2/C2saW2
i5+HWlAJtanO1IX6ra53wu669++RfX1/PACHyIE6sAdeK2mkVtV0ndaZY+74
cyqfmNPQiBsdY2dYZ88ZOefOn+fTxX1BL6uLcR3cuJt9c8yYmTUV83EH7pE7
dWfv/P32SD76j+VDfwrPgRW1BOv6Kr2qL/0dejffq1+fHbfzdscWnLjTcYR/
cYJ+xw==
"], 0.007682766082629425]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.007682766082629425], DiskBox[2, 0.007682766082629425], DiskBox[3, 0.007682766082629425], DiskBox[4, 0.007682766082629425], DiskBox[5, 0.007682766082629425], DiskBox[6, 0.007682766082629425], DiskBox[7, 0.007682766082629425], DiskBox[8, 0.007682766082629425], DiskBox[9, 0.007682766082629425], DiskBox[10, 0.007682766082629425], DiskBox[11, 0.007682766082629425], DiskBox[12, 0.007682766082629425], DiskBox[13, 0.007682766082629425], DiskBox[14, 0.007682766082629425], DiskBox[15, 0.007682766082629425], DiskBox[16, 0.007682766082629425], DiskBox[17, 0.007682766082629425], DiskBox[18, 0.007682766082629425], DiskBox[19, 0.007682766082629425], DiskBox[20, 0.007682766082629425], DiskBox[21, 0.007682766082629425], DiskBox[22, 0.007682766082629425], DiskBox[23, 0.007682766082629425], DiskBox[24, 0.007682766082629425], DiskBox[25, 0.007682766082629425], DiskBox[26, 0.007682766082629425], DiskBox[27, 0.007682766082629425], DiskBox[28, 0.007682766082629425], DiskBox[29, 0.007682766082629425], DiskBox[30, 0.007682766082629425], DiskBox[31, 0.007682766082629425], DiskBox[32, 0.007682766082629425], DiskBox[33, 0.007682766082629425], DiskBox[34, 0.007682766082629425], DiskBox[35, 0.007682766082629425], DiskBox[36, 0.007682766082629425], DiskBox[37, 0.007682766082629425], DiskBox[38, 0.007682766082629425], DiskBox[39, 0.007682766082629425], DiskBox[40, 0.007682766082629425], DiskBox[41, 0.007682766082629425], DiskBox[42, 0.007682766082629425], DiskBox[43, 0.007682766082629425], DiskBox[44, 0.007682766082629425], DiskBox[45, 0.007682766082629425], DiskBox[46, 0.007682766082629425], DiskBox[47, 0.007682766082629425], DiskBox[48, 0.007682766082629425], DiskBox[49, 0.007682766082629425], DiskBox[50, 0.007682766082629425], DiskBox[51, 0.007682766082629425], DiskBox[52, 0.007682766082629425], DiskBox[53, 0.007682766082629425], DiskBox[54, 0.007682766082629425], DiskBox[55, 0.007682766082629425], DiskBox[56, 0.007682766082629425], DiskBox[57, 0.007682766082629425], DiskBox[58, 0.007682766082629425], DiskBox[59, 0.007682766082629425], DiskBox[60, 0.007682766082629425], DiskBox[61, 0.007682766082629425], DiskBox[62, 0.007682766082629425], DiskBox[63, 0.007682766082629425], DiskBox[64, 0.007682766082629425], DiskBox[65, 0.007682766082629425], DiskBox[66, 0.007682766082629425], DiskBox[67, 0.007682766082629425], DiskBox[68, 0.007682766082629425], DiskBox[69, 0.007682766082629425], DiskBox[70, 0.007682766082629425], DiskBox[71, 0.007682766082629425], DiskBox[72, 0.007682766082629425], DiskBox[73, 0.007682766082629425], DiskBox[74, 0.007682766082629425], DiskBox[75, 0.007682766082629425], DiskBox[76, 0.007682766082629425], DiskBox[77, 0.007682766082629425], DiskBox[78, 0.007682766082629425], DiskBox[79, 0.007682766082629425], DiskBox[80, 0.007682766082629425], DiskBox[81, 0.007682766082629425], DiskBox[82, 0.007682766082629425], DiskBox[83, 0.007682766082629425], DiskBox[84, 0.007682766082629425], DiskBox[85, 0.007682766082629425], DiskBox[86, 0.007682766082629425], DiskBox[87, 0.007682766082629425], DiskBox[88, 0.007682766082629425], DiskBox[89, 0.007682766082629425], DiskBox[90, 0.007682766082629425], DiskBox[91, 0.007682766082629425], DiskBox[92, 0.007682766082629425], DiskBox[93, 0.007682766082629425], DiskBox[94, 0.007682766082629425], DiskBox[95, 0.007682766082629425], DiskBox[96, 0.007682766082629425], DiskBox[97, 0.007682766082629425], DiskBox[98, 0.007682766082629425], DiskBox[99, 0.007682766082629425], DiskBox[100, 0.007682766082629425]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
SparseArray[
Automatic, {23, 23}, 0, {1, {{0, 2, 5, 6, 7, 7, 10, 12, 12, 15, 19, 19, 22, 24, 26, 29, 29, 32, 34, 35, 35, 36, 39, 41}, {{5}, {16}, {
1}, {7}, {21}, {13}, {8}, {12}, {14}, {22}, {5}, {16}, {
2}, {3}, {18}, {2}, {3}, {18}, {20}, {3}, {5}, {16}, {
4}, {11}, {9}, {20}, {9}, {12}, {22}, {6}, {10}, {15}, {
7}, {13}, {23}, {19}, {3}, {18}, {23}, {5}, {16}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.04146110156920305], ArrowBox[{1, 5}, 0.0036549079020560286`], ArrowBox[{1, 16}, 0.0036549079020560286`], ArrowBox[{2, 1}, 0.0036549079020560286`], ArrowBox[{2, 7}, 0.0036549079020560286`], ArrowBox[{2, 21}, 0.0036549079020560286`], ArrowBox[{3, 13}, 0.0036549079020560286`], ArrowBox[{4, 8}, 0.0036549079020560286`], ArrowBox[{6, 12}, 0.0036549079020560286`], ArrowBox[{6, 14}, 0.0036549079020560286`], ArrowBox[{6, 22}, 0.0036549079020560286`], ArrowBox[{7, 5}, 0.0036549079020560286`], ArrowBox[{7, 16}, 0.0036549079020560286`], ArrowBox[{9, 2}, 0.0036549079020560286`], ArrowBox[{9, 3}, 0.0036549079020560286`], ArrowBox[{9, 18}, 0.0036549079020560286`], ArrowBox[{10, 2}, 0.0036549079020560286`], ArrowBox[{10, 3}, 0.0036549079020560286`], ArrowBox[{10, 18}, 0.0036549079020560286`], ArrowBox[{10, 20}, 0.0036549079020560286`], ArrowBox[{12, 3}, 0.0036549079020560286`], ArrowBox[{12, 5}, 0.0036549079020560286`], ArrowBox[{12, 16}, 0.0036549079020560286`], ArrowBox[{13, 4}, 0.0036549079020560286`], ArrowBox[{13, 11}, 0.0036549079020560286`], ArrowBox[{14, 9}, 0.0036549079020560286`], ArrowBox[{14, 20}, 0.0036549079020560286`], ArrowBox[{15, 9}, 0.0036549079020560286`], ArrowBox[{15, 12}, 0.0036549079020560286`], ArrowBox[{15, 22}, 0.0036549079020560286`], ArrowBox[{17, 6}, 0.0036549079020560286`], ArrowBox[{17, 10}, 0.0036549079020560286`], ArrowBox[{17, 15}, 0.0036549079020560286`], ArrowBox[{18, 7}, 0.0036549079020560286`], ArrowBox[{18, 13}, 0.0036549079020560286`], ArrowBox[{19, 23}, 0.0036549079020560286`], ArrowBox[{21, 19}, 0.0036549079020560286`], ArrowBox[{22, 3}, 0.0036549079020560286`], ArrowBox[{22, 18}, 0.0036549079020560286`], ArrowBox[{22, 23}, 0.0036549079020560286`], ArrowBox[{23, 5}, 0.0036549079020560286`], ArrowBox[{23, 16}, 0.0036549079020560286`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.0036549079020560286], DiskBox[2, 0.0036549079020560286], DiskBox[3, 0.0036549079020560286], DiskBox[4, 0.0036549079020560286], DiskBox[5, 0.0036549079020560286], DiskBox[6, 0.0036549079020560286], DiskBox[7, 0.0036549079020560286], DiskBox[8, 0.0036549079020560286], DiskBox[9, 0.0036549079020560286], DiskBox[10, 0.0036549079020560286], DiskBox[11, 0.0036549079020560286], DiskBox[12, 0.0036549079020560286], DiskBox[13, 0.0036549079020560286], DiskBox[14, 0.0036549079020560286], DiskBox[15, 0.0036549079020560286], DiskBox[16, 0.0036549079020560286], DiskBox[17, 0.0036549079020560286], DiskBox[18, 0.0036549079020560286], DiskBox[19, 0.0036549079020560286], DiskBox[20, 0.0036549079020560286], DiskBox[21, 0.0036549079020560286], DiskBox[22, 0.0036549079020560286], DiskBox[23, 0.0036549079020560286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), 2, "CausalSubgraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/7471dfd196c51758.png)
![ResourceFunction["CausalGraphEntanglementEntropyNaive"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
SparseArray[Automatic, {100, 100}, 0, {1, {CompressedData["
1:eJwt0L8rxHEAgOGvcuVX3XAldadOyXAKUVcuXZSSRblFyaWIwXAki5LSTTdY
LDZdBlcWk4nFIFJSyiLdIIPFwKYbeOo+bz3/wNu3slkotURRtBY1i9FOJ3ES
dJMkzQAZBhlmlGyQY4I8k0wzwyxzzLPAIksUWWaVdTYoBVtss8Mue+xzQJkK
hxxxzAlVTjmjxjkXwSVXXHPDLXfBPQ888sQzL8Erb9R554NPvvjmh18a/NFq
ZhsddBEnQQ8peknTT4YhRhgjyzg58kzxD6YDLiw=
"], CompressedData["
1:eJwdj1lTglAAhXFJ3MEIRiVATMRMGzavIoLhQuJUNOCGjGLqe///LXLmPH5n
Y8+/7jkOQZAZg6BIUJJ4elvRdY4nRjhpeUXq4yuerCQbrfaqSDFaUGT6mu2l
0Mf1N6sMJplmoIw31zon+vz4VUXURKPl8bMQ6PlCubOLdaUoy3JDRPWFkYGo
D87xFPFwzrBpzQzSfYIkjoKyuVwF0SFIzPjBrSxTe17uUujAhBlFCwRx5oRF
psn3+nvgAx0uVe0qJoObixJEJYor0Zztzm5kCa9aol+/H6YzF8llpq6kBXA2
N9wiPL1l5cG0Pf5vL5TNySn/0p0famxnOn9fAj+FtlexQlfqNfiWJ4jkJyca
mOyECZR8XMcri42uXK5R+eEG7fGR5QEdAX70ONdZ3GGUDKJZf1lFQCA=
"]}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.032577280450710414`], ArrowBox[CompressedData["
1:eJwVxVmbqQAAAFDZkiUZa4ySQbaotJF9G2FCkSXE1Pv8/7f73fNyiN8/7dft
crkmgMv1f8ALpIAvYAwc3Zi76C67SU/K0/cmvTnv0qv7YF/et/Wpfrff60dB
L1gCq2AdPAbgQD6AB+SACcEQDomQDCmQHvQHkeBn8BTah4kwF5bC0wgUqURM
mINHsAE7SBEpIwxyjZGx0UfroxuPxrsJT6KUqCb0JJmcJ62UkBqkw+lIOpNu
pi8ZIENlWBRDi2gZXaIaamWj2W72mqNz/c9hPprvYglshz2xFz7CDdwpgIVQ
YVhQCIyQiQlhfgW+xFKqlCunys8KXeEqRsWuOCRNMuSumqrmavHasPauJ+vL
RrCBNwqNWmPduDT9TaQpNScUSOEUR8mU2aJbTGve2rWsNtzG25U22ebbYvtG
C/SVEZgBC7IxNssqnSwX5zqcwNM8xxu8zTtiXqRFRuREQ3QkUIpJmFSWFEnr
znt0j+nNe7ueJcfkpJyVl32mfx0WRx+j3jgwhsb2hJ1oU3w6m2ozdibPzAW4
CC5Ci97ivIwuyW/s+7wiVp2VtJopdWW0Bteh9XCtbCKbzGaymW5e2/C2saW2
i5+HWlAJtanO1IX6ra53wu669++RfX1/PACHyIE6sAdeK2mkVtV0ndaZY+74
cyqfmNPQiBsdY2dYZ88ZOefOn+fTxX1BL6uLcR3cuJt9c8yYmTUV83EH7pE7
dWfv/P32SD76j+VDfwrPgRW1BOv6Kr2qL/0dejffq1+fHbfzdscWnLjTcYR/
cYJ+xw==
"], 0.007682766082629425]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.007682766082629425], DiskBox[2, 0.007682766082629425], DiskBox[3, 0.007682766082629425], DiskBox[4, 0.007682766082629425], DiskBox[5, 0.007682766082629425], DiskBox[6, 0.007682766082629425], DiskBox[7, 0.007682766082629425], DiskBox[8, 0.007682766082629425], DiskBox[9, 0.007682766082629425], DiskBox[10, 0.007682766082629425], DiskBox[11, 0.007682766082629425], DiskBox[12, 0.007682766082629425], DiskBox[13, 0.007682766082629425], DiskBox[14, 0.007682766082629425], DiskBox[15, 0.007682766082629425], DiskBox[16, 0.007682766082629425], DiskBox[17, 0.007682766082629425], DiskBox[18, 0.007682766082629425], DiskBox[19, 0.007682766082629425], DiskBox[20, 0.007682766082629425], DiskBox[21, 0.007682766082629425], DiskBox[22, 0.007682766082629425], DiskBox[23, 0.007682766082629425], DiskBox[24, 0.007682766082629425], DiskBox[25, 0.007682766082629425], DiskBox[26, 0.007682766082629425], DiskBox[27, 0.007682766082629425], DiskBox[28, 0.007682766082629425], DiskBox[29, 0.007682766082629425], DiskBox[30, 0.007682766082629425], DiskBox[31, 0.007682766082629425], DiskBox[32, 0.007682766082629425], DiskBox[33, 0.007682766082629425], DiskBox[34, 0.007682766082629425], DiskBox[35, 0.007682766082629425], DiskBox[36, 0.007682766082629425], DiskBox[37, 0.007682766082629425], DiskBox[38, 0.007682766082629425], DiskBox[39, 0.007682766082629425], DiskBox[40, 0.007682766082629425], DiskBox[41, 0.007682766082629425], DiskBox[42, 0.007682766082629425], DiskBox[43, 0.007682766082629425], DiskBox[44, 0.007682766082629425], DiskBox[45, 0.007682766082629425], DiskBox[46, 0.007682766082629425], DiskBox[47, 0.007682766082629425], DiskBox[48, 0.007682766082629425], DiskBox[49, 0.007682766082629425], DiskBox[50, 0.007682766082629425], DiskBox[51, 0.007682766082629425], DiskBox[52, 0.007682766082629425], DiskBox[53, 0.007682766082629425], DiskBox[54, 0.007682766082629425], DiskBox[55, 0.007682766082629425], DiskBox[56, 0.007682766082629425], DiskBox[57, 0.007682766082629425], DiskBox[58, 0.007682766082629425], DiskBox[59, 0.007682766082629425], DiskBox[60, 0.007682766082629425], DiskBox[61, 0.007682766082629425], DiskBox[62, 0.007682766082629425], DiskBox[63, 0.007682766082629425], DiskBox[64, 0.007682766082629425], DiskBox[65, 0.007682766082629425], DiskBox[66, 0.007682766082629425], DiskBox[67, 0.007682766082629425], DiskBox[68, 0.007682766082629425], DiskBox[69, 0.007682766082629425], DiskBox[70, 0.007682766082629425], DiskBox[71, 0.007682766082629425], DiskBox[72, 0.007682766082629425], DiskBox[73, 0.007682766082629425], DiskBox[74, 0.007682766082629425], DiskBox[75, 0.007682766082629425], DiskBox[76, 0.007682766082629425], DiskBox[77, 0.007682766082629425], DiskBox[78, 0.007682766082629425], DiskBox[79, 0.007682766082629425], DiskBox[80, 0.007682766082629425], DiskBox[81, 0.007682766082629425], DiskBox[82, 0.007682766082629425], DiskBox[83, 0.007682766082629425], DiskBox[84, 0.007682766082629425], DiskBox[85, 0.007682766082629425], DiskBox[86, 0.007682766082629425], DiskBox[87, 0.007682766082629425], DiskBox[88, 0.007682766082629425], DiskBox[89, 0.007682766082629425], DiskBox[90, 0.007682766082629425], DiskBox[91, 0.007682766082629425], DiskBox[92, 0.007682766082629425], DiskBox[93, 0.007682766082629425], DiskBox[94, 0.007682766082629425], DiskBox[95, 0.007682766082629425], DiskBox[96, 0.007682766082629425], DiskBox[97, 0.007682766082629425], DiskBox[98, 0.007682766082629425], DiskBox[99, 0.007682766082629425], DiskBox[100, 0.007682766082629425]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
SparseArray[
Automatic, {23, 23}, 0, {1, {{0, 2, 5, 6, 7, 7, 10, 12, 12, 15, 19, 19, 22, 24, 26, 29, 29, 32, 34, 35, 35, 36, 39, 41}, {{5}, {16}, {
1}, {7}, {21}, {13}, {8}, {12}, {14}, {22}, {5}, {16}, {
2}, {3}, {18}, {2}, {3}, {18}, {20}, {3}, {5}, {16}, {
4}, {11}, {9}, {20}, {9}, {12}, {22}, {6}, {10}, {15}, {
7}, {13}, {23}, {19}, {3}, {18}, {23}, {5}, {16}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.04146110156920305], ArrowBox[{1, 5}, 0.0036549079020560286`], ArrowBox[{1, 16}, 0.0036549079020560286`], ArrowBox[{2, 1}, 0.0036549079020560286`], ArrowBox[{2, 7}, 0.0036549079020560286`], ArrowBox[{2, 21}, 0.0036549079020560286`], ArrowBox[{3, 13}, 0.0036549079020560286`], ArrowBox[{4, 8}, 0.0036549079020560286`], ArrowBox[{6, 12}, 0.0036549079020560286`], ArrowBox[{6, 14}, 0.0036549079020560286`], ArrowBox[{6, 22}, 0.0036549079020560286`], ArrowBox[{7, 5}, 0.0036549079020560286`], ArrowBox[{7, 16}, 0.0036549079020560286`], ArrowBox[{9, 2}, 0.0036549079020560286`], ArrowBox[{9, 3}, 0.0036549079020560286`], ArrowBox[{9, 18}, 0.0036549079020560286`], ArrowBox[{10, 2}, 0.0036549079020560286`], ArrowBox[{10, 3}, 0.0036549079020560286`], ArrowBox[{10, 18}, 0.0036549079020560286`], ArrowBox[{10, 20}, 0.0036549079020560286`], ArrowBox[{12, 3}, 0.0036549079020560286`], ArrowBox[{12, 5}, 0.0036549079020560286`], ArrowBox[{12, 16}, 0.0036549079020560286`], ArrowBox[{13, 4}, 0.0036549079020560286`], ArrowBox[{13, 11}, 0.0036549079020560286`], ArrowBox[{14, 9}, 0.0036549079020560286`], ArrowBox[{14, 20}, 0.0036549079020560286`], ArrowBox[{15, 9}, 0.0036549079020560286`], ArrowBox[{15, 12}, 0.0036549079020560286`], ArrowBox[{15, 22}, 0.0036549079020560286`], ArrowBox[{17, 6}, 0.0036549079020560286`], ArrowBox[{17, 10}, 0.0036549079020560286`], ArrowBox[{17, 15}, 0.0036549079020560286`], ArrowBox[{18, 7}, 0.0036549079020560286`], ArrowBox[{18, 13}, 0.0036549079020560286`], ArrowBox[{19, 23}, 0.0036549079020560286`], ArrowBox[{21, 19}, 0.0036549079020560286`], ArrowBox[{22, 3}, 0.0036549079020560286`], ArrowBox[{22, 18}, 0.0036549079020560286`], ArrowBox[{22, 23}, 0.0036549079020560286`], ArrowBox[{23, 5}, 0.0036549079020560286`], ArrowBox[{23, 16}, 0.0036549079020560286`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.0036549079020560286], DiskBox[2, 0.0036549079020560286], DiskBox[3, 0.0036549079020560286], DiskBox[4, 0.0036549079020560286], DiskBox[5, 0.0036549079020560286], DiskBox[6, 0.0036549079020560286], DiskBox[7, 0.0036549079020560286], DiskBox[8, 0.0036549079020560286], DiskBox[9, 0.0036549079020560286], DiskBox[10, 0.0036549079020560286], DiskBox[11, 0.0036549079020560286], DiskBox[12, 0.0036549079020560286], DiskBox[13, 0.0036549079020560286], DiskBox[14, 0.0036549079020560286], DiskBox[15, 0.0036549079020560286], DiskBox[16, 0.0036549079020560286], DiskBox[17, 0.0036549079020560286], DiskBox[18, 0.0036549079020560286], DiskBox[19, 0.0036549079020560286], DiskBox[20, 0.0036549079020560286], DiskBox[21, 0.0036549079020560286], DiskBox[22, 0.0036549079020560286], DiskBox[23, 0.0036549079020560286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), 2, "FullCausalSubgraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/2689db282722b67e.png)
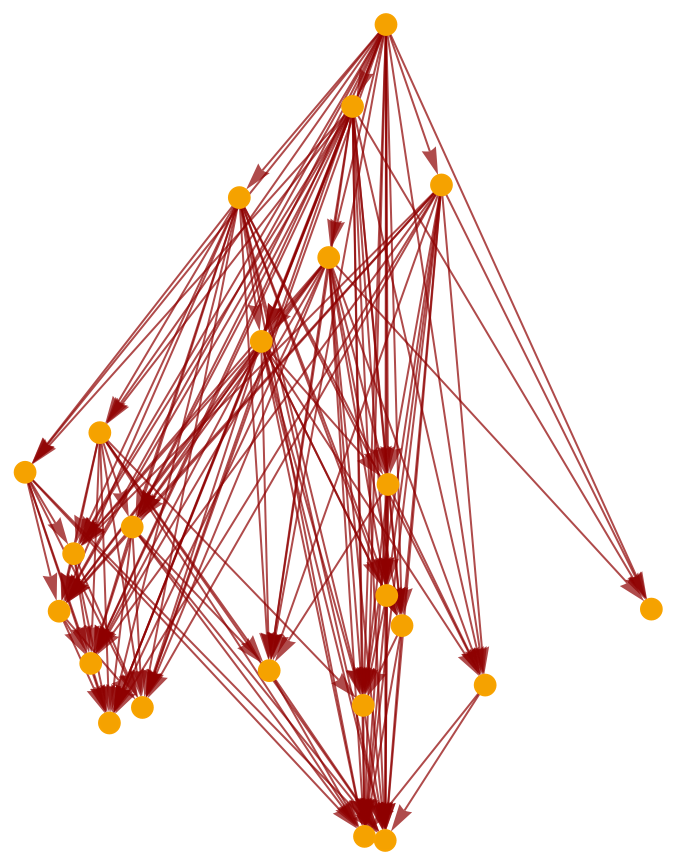
![ResourceFunction["CausalGraphEntanglementEntropyNaive"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
SparseArray[Automatic, {100, 100}, 0, {1, {CompressedData["
1:eJwt0L8rxHEAgOGvcuVX3XAldadOyXAKUVcuXZSSRblFyaWIwXAki5LSTTdY
LDZdBlcWk4nFIFJSyiLdIIPFwKYbeOo+bz3/wNu3slkotURRtBY1i9FOJ3ES
dJMkzQAZBhlmlGyQY4I8k0wzwyxzzLPAIksUWWaVdTYoBVtss8Mue+xzQJkK
hxxxzAlVTjmjxjkXwSVXXHPDLXfBPQ888sQzL8Erb9R554NPvvjmh18a/NFq
ZhsddBEnQQ8peknTT4YhRhgjyzg58kzxD6YDLiw=
"], CompressedData["
1:eJwdj1lTglAAhXFJ3MEIRiVATMRMGzavIoLhQuJUNOCGjGLqe///LXLmPH5n
Y8+/7jkOQZAZg6BIUJJ4elvRdY4nRjhpeUXq4yuerCQbrfaqSDFaUGT6mu2l
0Mf1N6sMJplmoIw31zon+vz4VUXURKPl8bMQ6PlCubOLdaUoy3JDRPWFkYGo
D87xFPFwzrBpzQzSfYIkjoKyuVwF0SFIzPjBrSxTe17uUujAhBlFCwRx5oRF
psn3+nvgAx0uVe0qJoObixJEJYor0Zztzm5kCa9aol+/H6YzF8llpq6kBXA2
N9wiPL1l5cG0Pf5vL5TNySn/0p0famxnOn9fAj+FtlexQlfqNfiWJ4jkJyca
mOyECZR8XMcri42uXK5R+eEG7fGR5QEdAX70ONdZ3GGUDKJZf1lFQCA=
"]}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.032577280450710414`], ArrowBox[CompressedData["
1:eJwVxVmbqQAAAFDZkiUZa4ySQbaotJF9G2FCkSXE1Pv8/7f73fNyiN8/7dft
crkmgMv1f8ALpIAvYAwc3Zi76C67SU/K0/cmvTnv0qv7YF/et/Wpfrff60dB
L1gCq2AdPAbgQD6AB+SACcEQDomQDCmQHvQHkeBn8BTah4kwF5bC0wgUqURM
mINHsAE7SBEpIwxyjZGx0UfroxuPxrsJT6KUqCb0JJmcJ62UkBqkw+lIOpNu
pi8ZIENlWBRDi2gZXaIaamWj2W72mqNz/c9hPprvYglshz2xFz7CDdwpgIVQ
YVhQCIyQiQlhfgW+xFKqlCunys8KXeEqRsWuOCRNMuSumqrmavHasPauJ+vL
RrCBNwqNWmPduDT9TaQpNScUSOEUR8mU2aJbTGve2rWsNtzG25U22ebbYvtG
C/SVEZgBC7IxNssqnSwX5zqcwNM8xxu8zTtiXqRFRuREQ3QkUIpJmFSWFEnr
znt0j+nNe7ueJcfkpJyVl32mfx0WRx+j3jgwhsb2hJ1oU3w6m2ozdibPzAW4
CC5Ci97ivIwuyW/s+7wiVp2VtJopdWW0Bteh9XCtbCKbzGaymW5e2/C2saW2
i5+HWlAJtanO1IX6ra53wu669++RfX1/PACHyIE6sAdeK2mkVtV0ndaZY+74
cyqfmNPQiBsdY2dYZ88ZOefOn+fTxX1BL6uLcR3cuJt9c8yYmTUV83EH7pE7
dWfv/P32SD76j+VDfwrPgRW1BOv6Kr2qL/0dejffq1+fHbfzdscWnLjTcYR/
cYJ+xw==
"], 0.007682766082629425]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.007682766082629425], DiskBox[2, 0.007682766082629425], DiskBox[3, 0.007682766082629425], DiskBox[4, 0.007682766082629425], DiskBox[5, 0.007682766082629425], DiskBox[6, 0.007682766082629425], DiskBox[7, 0.007682766082629425], DiskBox[8, 0.007682766082629425], DiskBox[9, 0.007682766082629425], DiskBox[10, 0.007682766082629425], DiskBox[11, 0.007682766082629425], DiskBox[12, 0.007682766082629425], DiskBox[13, 0.007682766082629425], DiskBox[14, 0.007682766082629425], DiskBox[15, 0.007682766082629425], DiskBox[16, 0.007682766082629425], DiskBox[17, 0.007682766082629425], DiskBox[18, 0.007682766082629425], DiskBox[19, 0.007682766082629425], DiskBox[20, 0.007682766082629425], DiskBox[21, 0.007682766082629425], DiskBox[22, 0.007682766082629425], DiskBox[23, 0.007682766082629425], DiskBox[24, 0.007682766082629425], DiskBox[25, 0.007682766082629425], DiskBox[26, 0.007682766082629425], DiskBox[27, 0.007682766082629425], DiskBox[28, 0.007682766082629425], DiskBox[29, 0.007682766082629425], DiskBox[30, 0.007682766082629425], DiskBox[31, 0.007682766082629425], DiskBox[32, 0.007682766082629425], DiskBox[33, 0.007682766082629425], DiskBox[34, 0.007682766082629425], DiskBox[35, 0.007682766082629425], DiskBox[36, 0.007682766082629425], DiskBox[37, 0.007682766082629425], DiskBox[38, 0.007682766082629425], DiskBox[39, 0.007682766082629425], DiskBox[40, 0.007682766082629425], DiskBox[41, 0.007682766082629425], DiskBox[42, 0.007682766082629425], DiskBox[43, 0.007682766082629425], DiskBox[44, 0.007682766082629425], DiskBox[45, 0.007682766082629425], DiskBox[46, 0.007682766082629425], DiskBox[47, 0.007682766082629425], DiskBox[48, 0.007682766082629425], DiskBox[49, 0.007682766082629425], DiskBox[50, 0.007682766082629425], DiskBox[51, 0.007682766082629425], DiskBox[52, 0.007682766082629425], DiskBox[53, 0.007682766082629425], DiskBox[54, 0.007682766082629425], DiskBox[55, 0.007682766082629425], DiskBox[56, 0.007682766082629425], DiskBox[57, 0.007682766082629425], DiskBox[58, 0.007682766082629425], DiskBox[59, 0.007682766082629425], DiskBox[60, 0.007682766082629425], DiskBox[61, 0.007682766082629425], DiskBox[62, 0.007682766082629425], DiskBox[63, 0.007682766082629425], DiskBox[64, 0.007682766082629425], DiskBox[65, 0.007682766082629425], DiskBox[66, 0.007682766082629425], DiskBox[67, 0.007682766082629425], DiskBox[68, 0.007682766082629425], DiskBox[69, 0.007682766082629425], DiskBox[70, 0.007682766082629425], DiskBox[71, 0.007682766082629425], DiskBox[72, 0.007682766082629425], DiskBox[73, 0.007682766082629425], DiskBox[74, 0.007682766082629425], DiskBox[75, 0.007682766082629425], DiskBox[76, 0.007682766082629425], DiskBox[77, 0.007682766082629425], DiskBox[78, 0.007682766082629425], DiskBox[79, 0.007682766082629425], DiskBox[80, 0.007682766082629425], DiskBox[81, 0.007682766082629425], DiskBox[82, 0.007682766082629425], DiskBox[83, 0.007682766082629425], DiskBox[84, 0.007682766082629425], DiskBox[85, 0.007682766082629425], DiskBox[86, 0.007682766082629425], DiskBox[87, 0.007682766082629425], DiskBox[88, 0.007682766082629425], DiskBox[89, 0.007682766082629425], DiskBox[90, 0.007682766082629425], DiskBox[91, 0.007682766082629425], DiskBox[92, 0.007682766082629425], DiskBox[93, 0.007682766082629425], DiskBox[94, 0.007682766082629425], DiskBox[95, 0.007682766082629425], DiskBox[96, 0.007682766082629425], DiskBox[97, 0.007682766082629425], DiskBox[98, 0.007682766082629425], DiskBox[99, 0.007682766082629425], DiskBox[100, 0.007682766082629425]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
SparseArray[
Automatic, {23, 23}, 0, {1, {{0, 2, 5, 6, 7, 7, 10, 12, 12, 15, 19, 19, 22, 24, 26, 29, 29, 32, 34, 35, 35, 36, 39, 41}, {{5}, {16}, {
1}, {7}, {21}, {13}, {8}, {12}, {14}, {22}, {5}, {16}, {
2}, {3}, {18}, {2}, {3}, {18}, {20}, {3}, {5}, {16}, {
4}, {11}, {9}, {20}, {9}, {12}, {22}, {6}, {10}, {15}, {
7}, {13}, {23}, {19}, {3}, {18}, {23}, {5}, {16}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.04146110156920305], ArrowBox[{1, 5}, 0.0036549079020560286`], ArrowBox[{1, 16}, 0.0036549079020560286`], ArrowBox[{2, 1}, 0.0036549079020560286`], ArrowBox[{2, 7}, 0.0036549079020560286`], ArrowBox[{2, 21}, 0.0036549079020560286`], ArrowBox[{3, 13}, 0.0036549079020560286`], ArrowBox[{4, 8}, 0.0036549079020560286`], ArrowBox[{6, 12}, 0.0036549079020560286`], ArrowBox[{6, 14}, 0.0036549079020560286`], ArrowBox[{6, 22}, 0.0036549079020560286`], ArrowBox[{7, 5}, 0.0036549079020560286`], ArrowBox[{7, 16}, 0.0036549079020560286`], ArrowBox[{9, 2}, 0.0036549079020560286`], ArrowBox[{9, 3}, 0.0036549079020560286`], ArrowBox[{9, 18}, 0.0036549079020560286`], ArrowBox[{10, 2}, 0.0036549079020560286`], ArrowBox[{10, 3}, 0.0036549079020560286`], ArrowBox[{10, 18}, 0.0036549079020560286`], ArrowBox[{10, 20}, 0.0036549079020560286`], ArrowBox[{12, 3}, 0.0036549079020560286`], ArrowBox[{12, 5}, 0.0036549079020560286`], ArrowBox[{12, 16}, 0.0036549079020560286`], ArrowBox[{13, 4}, 0.0036549079020560286`], ArrowBox[{13, 11}, 0.0036549079020560286`], ArrowBox[{14, 9}, 0.0036549079020560286`], ArrowBox[{14, 20}, 0.0036549079020560286`], ArrowBox[{15, 9}, 0.0036549079020560286`], ArrowBox[{15, 12}, 0.0036549079020560286`], ArrowBox[{15, 22}, 0.0036549079020560286`], ArrowBox[{17, 6}, 0.0036549079020560286`], ArrowBox[{17, 10}, 0.0036549079020560286`], ArrowBox[{17, 15}, 0.0036549079020560286`], ArrowBox[{18, 7}, 0.0036549079020560286`], ArrowBox[{18, 13}, 0.0036549079020560286`], ArrowBox[{19, 23}, 0.0036549079020560286`], ArrowBox[{21, 19}, 0.0036549079020560286`], ArrowBox[{22, 3}, 0.0036549079020560286`], ArrowBox[{22, 18}, 0.0036549079020560286`], ArrowBox[{22, 23}, 0.0036549079020560286`], ArrowBox[{23, 5}, 0.0036549079020560286`], ArrowBox[{23, 16}, 0.0036549079020560286`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.0036549079020560286], DiskBox[2, 0.0036549079020560286], DiskBox[3, 0.0036549079020560286], DiskBox[4, 0.0036549079020560286], DiskBox[5, 0.0036549079020560286], DiskBox[6, 0.0036549079020560286], DiskBox[7, 0.0036549079020560286], DiskBox[8, 0.0036549079020560286], DiskBox[9, 0.0036549079020560286], DiskBox[10, 0.0036549079020560286], DiskBox[11, 0.0036549079020560286], DiskBox[12, 0.0036549079020560286], DiskBox[13, 0.0036549079020560286], DiskBox[14, 0.0036549079020560286], DiskBox[15, 0.0036549079020560286], DiskBox[16, 0.0036549079020560286], DiskBox[17, 0.0036549079020560286], DiskBox[18, 0.0036549079020560286], DiskBox[19, 0.0036549079020560286], DiskBox[20, 0.0036549079020560286], DiskBox[21, 0.0036549079020560286], DiskBox[22, 0.0036549079020560286], DiskBox[23, 0.0036549079020560286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), 2, "CausalGraphHighlighted"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/3ab82b6be00e51e1.png)
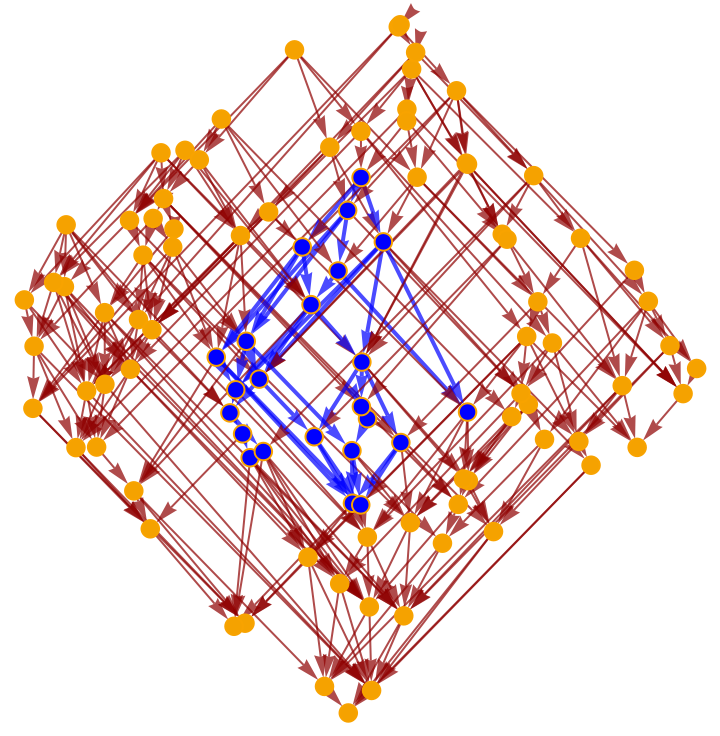
![ResourceFunction["CausalGraphEntanglementEntropyNaive"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
SparseArray[Automatic, {100, 100}, 0, {1, {CompressedData["
1:eJwt0L8rxHEAgOGvcuVX3XAldadOyXAKUVcuXZSSRblFyaWIwXAki5LSTTdY
LDZdBlcWk4nFIFJSyiLdIIPFwKYbeOo+bz3/wNu3slkotURRtBY1i9FOJ3ES
dJMkzQAZBhlmlGyQY4I8k0wzwyxzzLPAIksUWWaVdTYoBVtss8Mue+xzQJkK
hxxxzAlVTjmjxjkXwSVXXHPDLXfBPQ888sQzL8Erb9R554NPvvjmh18a/NFq
ZhsddBEnQQ8peknTT4YhRhgjyzg58kzxD6YDLiw=
"], CompressedData["
1:eJwdj1lTglAAhXFJ3MEIRiVATMRMGzavIoLhQuJUNOCGjGLqe///LXLmPH5n
Y8+/7jkOQZAZg6BIUJJ4elvRdY4nRjhpeUXq4yuerCQbrfaqSDFaUGT6mu2l
0Mf1N6sMJplmoIw31zon+vz4VUXURKPl8bMQ6PlCubOLdaUoy3JDRPWFkYGo
D87xFPFwzrBpzQzSfYIkjoKyuVwF0SFIzPjBrSxTe17uUujAhBlFCwRx5oRF
psn3+nvgAx0uVe0qJoObixJEJYor0Zztzm5kCa9aol+/H6YzF8llpq6kBXA2
N9wiPL1l5cG0Pf5vL5TNySn/0p0famxnOn9fAj+FtlexQlfqNfiWJ4jkJyca
mOyECZR8XMcri42uXK5R+eEG7fGR5QEdAX70ONdZ3GGUDKJZf1lFQCA=
"]}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwVk/0/FIYfwFHKHEqtm+eSqfVwJs9P+ZjHZb7n6ZbHkCLTN5QXzSTRQrqU
ua+HnHE2zlPOnTjOnQ/3QM7TuSSKMrvWPLSaZWOT1veH9+v9D7zfxtGJATEq
SkpKp9/zf3913mv1dY8IJ1cTl0I8e6FuPDPMSNEPem6sXYKtWcAqetjZqtwP
Qsxm+mS2YspK/mJnTiMkJE55km3uoct12eO9oQ3wyfZnBhFecgjeaR4l/KwP
zD0vPh8W14KL98AfKQQa7L5pObOon4Vku1lDBk+IW99Qrk00cGHmjFxfuq0P
/VUPbd79uA14xczILZqDYGnopmbD7ATX3caFGm5CeHN0hRNG5UFK99W/f8/K
QsYPxb/0qvdDSaZvriutHw94PX33likAx7w3dYWFffj6omL0BK0CsrcH5STY
tyGRnWuviB5Bs+MFRi94o2DzuXvypv4KND8Y+1bPl4sE30pdeU8Vdjjzh2bE
bVhNHM955spBOiVUsFQ8jErUnfm7Qtvwb6u1a6nmEiBv7JkJ+IKJsYv+x/z2
50JsSJRQd6kH53bR4jheveAyY29apydGz572rF6HH/GNq0p8+roMUk3GX2lm
IHofp47yKiVw+UhecJCyBIrpHPodMRU2h6QSy3X68Vtl64rG7Yj7dM6Zm9Xz
4M+V9OBsQi9+v6+mpUZ9HJ490dAo76Si01ffj5rajOEUxOfItOuRHnZbURMh
hvmxIzYJMdV4ZeeAvr62BJdby4xEF2lA4y6azCTx4bKBhc+giwRomYs1Qq0M
2P+ByDptHuEoPSX551YZJFpoxHn8pw2PfZP9u0WJELfUt6eT+V0QTGplnVrg
Q97p0yrhA3y8vS2cf2taChdIGpdwpRWTruufmZgbQVk4wTbt5l0Iii4TVCyX
QtZP4/N/csV4hZ1ilf+wC95tMr7md5KP54XZjVSHZjB77tPt6T8IEccTmoiS
YizNtn7nM8/BzuRL0ghSC1hWGvrPjY2CYvSlc0EcG2YTWu6vN4ng19axSKZz
O+qEm2q1ub7vI6E+T7DrHiq51510q+JirKKbPd4ygv6xtwtC6/kwUvSpWm33
HUjfYbbpp4Ih/K5S8LT6YRMsQ/WJR7eG8UcvVZcmRhm2qRG9izJqgBs7on3Q
YxAvRWgQMx3acMugR8XmmCGMrixx5fowsKH/15Vpggw70mZ8X6SxYPVm1z8U
pMMaNNox/pIjx/twSGiUFCOdKLpuzxmQGkk58h3zBwgvMToonegA1Z/ldDJI
8GGVZor7oAgVufMPjhmyMcWQTC1waMc01X75/5q70K9ci3uYlYQ77s/9Zq3L
BbJUYOASJ0HlE+Q2z5BMqPPSbLZ0HMeKyQXHDa8H4EFRJdJSq5G69ex0ckUH
frEqtfvAqBFHmleaQ1+K8Y+w/I5gnW5YKpxYc9L+EvU/1hrTInOAbS+5MTDF
wo9fXs/55ybCEzHzpEJUhZvcE2xaWrmQX26Wd47DxaKA/y7f6hrBUjuZokD6
vmP6hsNHT0Tw6ZXALJJ6EaxHyqZH9HoxIPBopB1VBgeolevuyRw4f+DUnh0B
ReAneTRkVSOC2W9s68vUOBj4qjo9ea4EczYOPtjfyYfth0zYC3slcNbCL+Zu
Hg9XCEwew1oK668e77H8kA1vNQjM+Ecy+Hy5xTPwozKYT5wuDGm/iy2UsqRX
n/Eg4YJqHPHkMCgdjg/P8jSA15kmxNXXA2jAmM2+OCiEYfbQmcTETqAs7M0w
CunFUp9oNQW7D5zWHV1C+e//+GvfRDG/AQOczQMC+ljwjptbcU5XhAZRD8wU
pUXgLphlnfCuw7PV8Ycab8hh7UJrsX/v11Cb4R6jlt6PqzRDUppKAT6dnCbw
KGOw8Mta7pertXAbfaZ8PymCLSbxUbPj92FS3UqnZ9sNrLK9k3JXIMcGQVyw
GnsMe7oF4RblTNhj6l2Uv3wP87QDnXysvgXSh+vPSQQxMlQSFA3xfSBOYhy6
4ZwDIlJi9Jp6O1JXjPy1HIegaeHZCx9yJ9qasC7xw+hIMBiuJaz3YW8H7wnb
XwRWk2kHPAab0I96VS9+bzOor0+uGCtL4fG5JQKL1Ai2QRsU2Wk5uGjOkE+Z
juH+y+qmSqmpYD/VQNscJEXDOWNSPJWO/wLmFzal
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.032577280450710414`], ArrowBox[CompressedData["
1:eJwVxVmbqQAAAFDZkiUZa4ySQbaotJF9G2FCkSXE1Pv8/7f73fNyiN8/7dft
crkmgMv1f8ALpIAvYAwc3Zi76C67SU/K0/cmvTnv0qv7YF/et/Wpfrff60dB
L1gCq2AdPAbgQD6AB+SACcEQDomQDCmQHvQHkeBn8BTah4kwF5bC0wgUqURM
mINHsAE7SBEpIwxyjZGx0UfroxuPxrsJT6KUqCb0JJmcJ62UkBqkw+lIOpNu
pi8ZIENlWBRDi2gZXaIaamWj2W72mqNz/c9hPprvYglshz2xFz7CDdwpgIVQ
YVhQCIyQiQlhfgW+xFKqlCunys8KXeEqRsWuOCRNMuSumqrmavHasPauJ+vL
RrCBNwqNWmPduDT9TaQpNScUSOEUR8mU2aJbTGve2rWsNtzG25U22ebbYvtG
C/SVEZgBC7IxNssqnSwX5zqcwNM8xxu8zTtiXqRFRuREQ3QkUIpJmFSWFEnr
znt0j+nNe7ueJcfkpJyVl32mfx0WRx+j3jgwhsb2hJ1oU3w6m2ozdibPzAW4
CC5Ci97ivIwuyW/s+7wiVp2VtJopdWW0Bteh9XCtbCKbzGaymW5e2/C2saW2
i5+HWlAJtanO1IX6ra53wu669++RfX1/PACHyIE6sAdeK2mkVtV0ndaZY+74
cyqfmNPQiBsdY2dYZ88ZOefOn+fTxX1BL6uLcR3cuJt9c8yYmTUV83EH7pE7
dWfv/P32SD76j+VDfwrPgRW1BOv6Kr2qL/0dejffq1+fHbfzdscWnLjTcYR/
cYJ+xw==
"], 0.007682766082629425]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.007682766082629425], DiskBox[2, 0.007682766082629425], DiskBox[3, 0.007682766082629425], DiskBox[4, 0.007682766082629425], DiskBox[5, 0.007682766082629425], DiskBox[6, 0.007682766082629425], DiskBox[7, 0.007682766082629425], DiskBox[8, 0.007682766082629425], DiskBox[9, 0.007682766082629425], DiskBox[10, 0.007682766082629425], DiskBox[11, 0.007682766082629425], DiskBox[12, 0.007682766082629425], DiskBox[13, 0.007682766082629425], DiskBox[14, 0.007682766082629425], DiskBox[15, 0.007682766082629425], DiskBox[16, 0.007682766082629425], DiskBox[17, 0.007682766082629425], DiskBox[18, 0.007682766082629425], DiskBox[19, 0.007682766082629425], DiskBox[20, 0.007682766082629425], DiskBox[21, 0.007682766082629425], DiskBox[22, 0.007682766082629425], DiskBox[23, 0.007682766082629425], DiskBox[24, 0.007682766082629425], DiskBox[25, 0.007682766082629425], DiskBox[26, 0.007682766082629425], DiskBox[27, 0.007682766082629425], DiskBox[28, 0.007682766082629425], DiskBox[29, 0.007682766082629425], DiskBox[30, 0.007682766082629425], DiskBox[31, 0.007682766082629425], DiskBox[32, 0.007682766082629425], DiskBox[33, 0.007682766082629425], DiskBox[34, 0.007682766082629425], DiskBox[35, 0.007682766082629425], DiskBox[36, 0.007682766082629425], DiskBox[37, 0.007682766082629425], DiskBox[38, 0.007682766082629425], DiskBox[39, 0.007682766082629425], DiskBox[40, 0.007682766082629425], DiskBox[41, 0.007682766082629425], DiskBox[42, 0.007682766082629425], DiskBox[43, 0.007682766082629425], DiskBox[44, 0.007682766082629425], DiskBox[45, 0.007682766082629425], DiskBox[46, 0.007682766082629425], DiskBox[47, 0.007682766082629425], DiskBox[48, 0.007682766082629425], DiskBox[49, 0.007682766082629425], DiskBox[50, 0.007682766082629425], DiskBox[51, 0.007682766082629425], DiskBox[52, 0.007682766082629425], DiskBox[53, 0.007682766082629425], DiskBox[54, 0.007682766082629425], DiskBox[55, 0.007682766082629425], DiskBox[56, 0.007682766082629425], DiskBox[57, 0.007682766082629425], DiskBox[58, 0.007682766082629425], DiskBox[59, 0.007682766082629425], DiskBox[60, 0.007682766082629425], DiskBox[61, 0.007682766082629425], DiskBox[62, 0.007682766082629425], DiskBox[63, 0.007682766082629425], DiskBox[64, 0.007682766082629425], DiskBox[65, 0.007682766082629425], DiskBox[66, 0.007682766082629425], DiskBox[67, 0.007682766082629425], DiskBox[68, 0.007682766082629425], DiskBox[69, 0.007682766082629425], DiskBox[70, 0.007682766082629425], DiskBox[71, 0.007682766082629425], DiskBox[72, 0.007682766082629425], DiskBox[73, 0.007682766082629425], DiskBox[74, 0.007682766082629425], DiskBox[75, 0.007682766082629425], DiskBox[76, 0.007682766082629425], DiskBox[77, 0.007682766082629425], DiskBox[78, 0.007682766082629425], DiskBox[79, 0.007682766082629425], DiskBox[80, 0.007682766082629425], DiskBox[81, 0.007682766082629425], DiskBox[82, 0.007682766082629425], DiskBox[83, 0.007682766082629425], DiskBox[84, 0.007682766082629425], DiskBox[85, 0.007682766082629425], DiskBox[86, 0.007682766082629425], DiskBox[87, 0.007682766082629425], DiskBox[88, 0.007682766082629425], DiskBox[89, 0.007682766082629425], DiskBox[90, 0.007682766082629425], DiskBox[91, 0.007682766082629425], DiskBox[92, 0.007682766082629425], DiskBox[93, 0.007682766082629425], DiskBox[94, 0.007682766082629425], DiskBox[95, 0.007682766082629425], DiskBox[96, 0.007682766082629425], DiskBox[97, 0.007682766082629425], DiskBox[98, 0.007682766082629425], DiskBox[99, 0.007682766082629425], DiskBox[100, 0.007682766082629425]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
SparseArray[
Automatic, {23, 23}, 0, {1, {{0, 2, 5, 6, 7, 7, 10, 12, 12, 15, 19, 19, 22, 24, 26, 29, 29, 32, 34, 35, 35, 36, 39, 41}, {{5}, {16}, {
1}, {7}, {21}, {13}, {8}, {12}, {14}, {22}, {5}, {16}, {
2}, {3}, {18}, {2}, {3}, {18}, {20}, {3}, {5}, {16}, {
4}, {11}, {9}, {20}, {9}, {12}, {22}, {6}, {10}, {15}, {
7}, {13}, {23}, {19}, {3}, {18}, {23}, {5}, {16}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"]}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJwBgQF+/iFib1JlAgAAABcAAAACAAAAdfWK67mGqz9ub9lGTja0v0BKyfN1
C5Q/H40z3esbgb8wKmb9Gk+3vwtPnxnSwKC/uD68zN3Etb+iFtSG30Kyv2br
UUlQJ4c/ZllgwhnswL+Uf+ulwg59PycJwzV56b8/XlZurBbFlr+YgjX/TOmy
v3VuqYi9FbS/AESoYUOgt7+kRwVArKGZv7UIFkqTfaU/dl9UMZKnoz9clx4q
yta4P+SH6dNJHbG/dR1OjI46tr95BcfSla67v1CbDrcsr3C/jAdr3HOduL9L
+Mo4CR6rv+yR1vk8EVW/GyQO0Q5Osj/bxKdh5MOgvwNEbjaws7c/L4BTgS0K
kz/8X9DczhrBv3EpYyASUpM/UMXXzDSlwz/gejepmQiyv1Pvontz4pe/SPKw
RlMXmT/pb9yRWbatvzz8O0BavLw/fvcm1pa8qr8cYNMu5JiTP0S94K9dSqi/
ICVKk4rytL+IEVM8TDSEP8RwoSuLPoY/wy1vYvkKtr8P97yM
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[0.04146110156920305], ArrowBox[{1, 5}, 0.0036549079020560286`], ArrowBox[{1, 16}, 0.0036549079020560286`], ArrowBox[{2, 1}, 0.0036549079020560286`], ArrowBox[{2, 7}, 0.0036549079020560286`], ArrowBox[{2, 21}, 0.0036549079020560286`], ArrowBox[{3, 13}, 0.0036549079020560286`], ArrowBox[{4, 8}, 0.0036549079020560286`], ArrowBox[{6, 12}, 0.0036549079020560286`], ArrowBox[{6, 14}, 0.0036549079020560286`], ArrowBox[{6, 22}, 0.0036549079020560286`], ArrowBox[{7, 5}, 0.0036549079020560286`], ArrowBox[{7, 16}, 0.0036549079020560286`], ArrowBox[{9, 2}, 0.0036549079020560286`], ArrowBox[{9, 3}, 0.0036549079020560286`], ArrowBox[{9, 18}, 0.0036549079020560286`], ArrowBox[{10, 2}, 0.0036549079020560286`], ArrowBox[{10, 3}, 0.0036549079020560286`], ArrowBox[{10, 18}, 0.0036549079020560286`], ArrowBox[{10, 20}, 0.0036549079020560286`], ArrowBox[{12, 3}, 0.0036549079020560286`], ArrowBox[{12, 5}, 0.0036549079020560286`], ArrowBox[{12, 16}, 0.0036549079020560286`], ArrowBox[{13, 4}, 0.0036549079020560286`], ArrowBox[{13, 11}, 0.0036549079020560286`], ArrowBox[{14, 9}, 0.0036549079020560286`], ArrowBox[{14, 20}, 0.0036549079020560286`], ArrowBox[{15, 9}, 0.0036549079020560286`], ArrowBox[{15, 12}, 0.0036549079020560286`], ArrowBox[{15, 22}, 0.0036549079020560286`], ArrowBox[{17, 6}, 0.0036549079020560286`], ArrowBox[{17, 10}, 0.0036549079020560286`], ArrowBox[{17, 15}, 0.0036549079020560286`], ArrowBox[{18, 7}, 0.0036549079020560286`], ArrowBox[{18, 13}, 0.0036549079020560286`], ArrowBox[{19, 23}, 0.0036549079020560286`], ArrowBox[{21, 19}, 0.0036549079020560286`], ArrowBox[{22, 3}, 0.0036549079020560286`], ArrowBox[{22, 18}, 0.0036549079020560286`], ArrowBox[{22, 23}, 0.0036549079020560286`], ArrowBox[{23, 5}, 0.0036549079020560286`], ArrowBox[{23, 16}, 0.0036549079020560286`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.0036549079020560286], DiskBox[2, 0.0036549079020560286], DiskBox[3, 0.0036549079020560286], DiskBox[4, 0.0036549079020560286], DiskBox[5, 0.0036549079020560286], DiskBox[6, 0.0036549079020560286], DiskBox[7, 0.0036549079020560286], DiskBox[8, 0.0036549079020560286], DiskBox[9, 0.0036549079020560286], DiskBox[10, 0.0036549079020560286], DiskBox[11, 0.0036549079020560286], DiskBox[12, 0.0036549079020560286], DiskBox[13, 0.0036549079020560286], DiskBox[14, 0.0036549079020560286], DiskBox[15, 0.0036549079020560286], DiskBox[16, 0.0036549079020560286], DiskBox[17, 0.0036549079020560286], DiskBox[18, 0.0036549079020560286], DiskBox[19, 0.0036549079020560286], DiskBox[20, 0.0036549079020560286], DiskBox[21, 0.0036549079020560286], DiskBox[22, 0.0036549079020560286], DiskBox[23, 0.0036549079020560286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), 2, "FullCausalGraphHighlighted"]](https://www.wolframcloud.com/obj/resourcesystem/images/470/470a040e-480c-4ae0-b573-a97ff07070e7/01c64fe69d5aec7e.png)