Basic Examples (4)
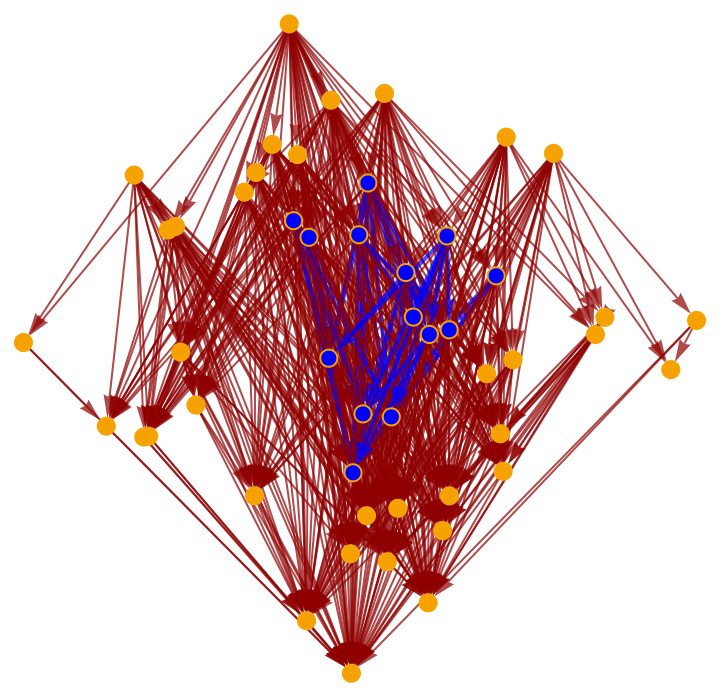
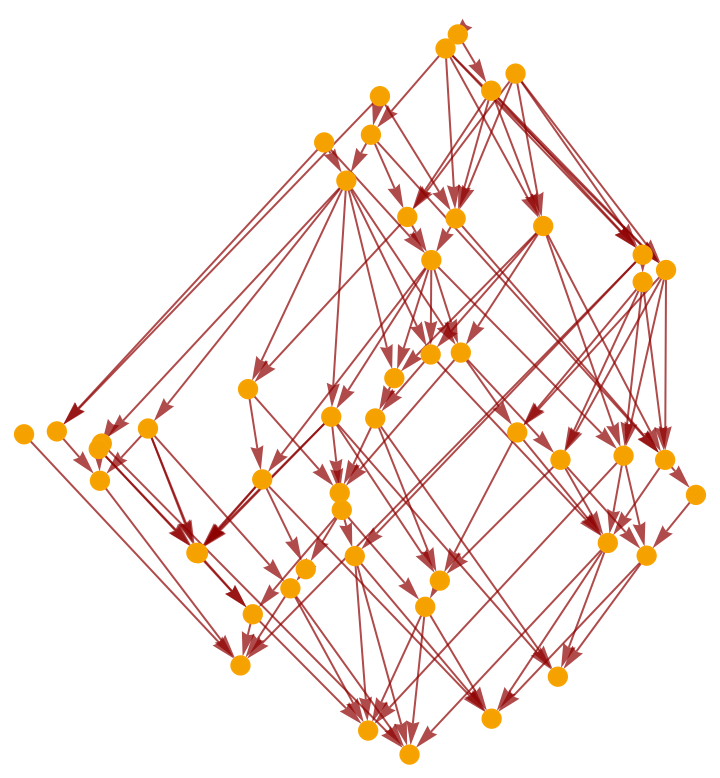
Construct a causal graph by randomly sprinkling 50 points within a diamond-shaped region of 1+1-dimensional Minkowski space:
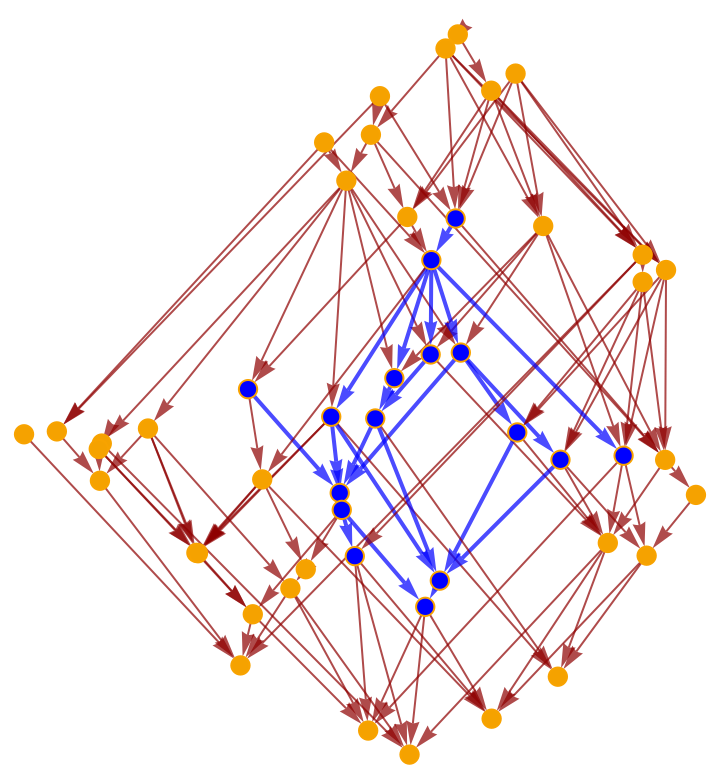
Construct a subgraph of this causal graph corresponding to a smaller, interior diamond region:
Compute the entanglement entropy associated with this subgraph using the generalized approach:
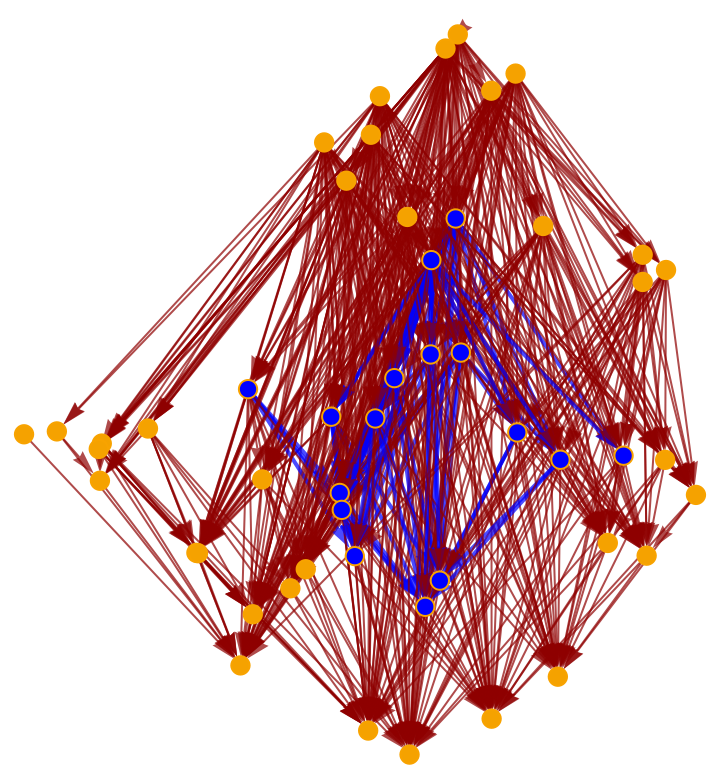
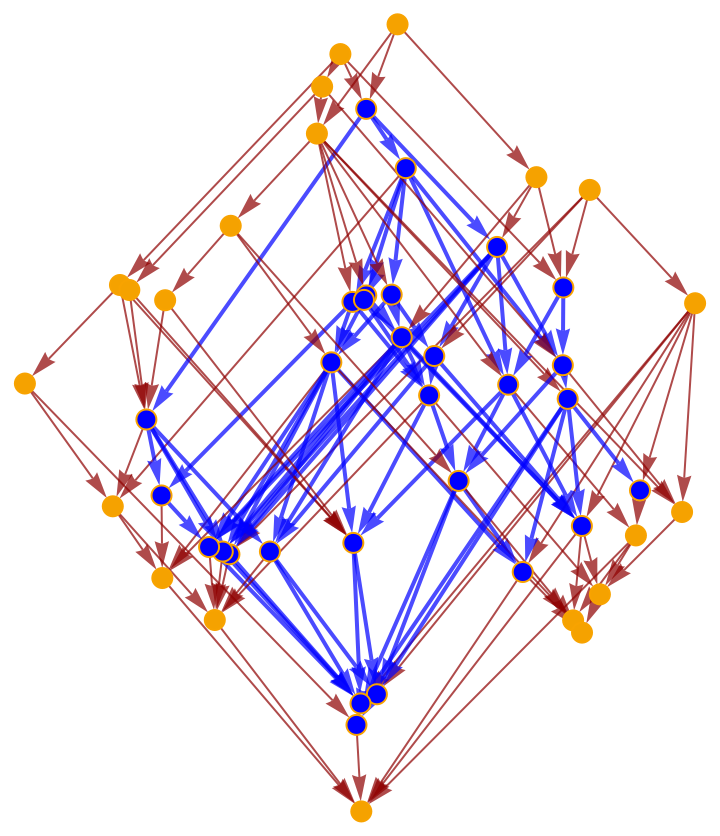
Highlight the interior subgraph within the larger (transitively reduced) causal graph:
Highlight the interior subgraph within the full (i.e. transitively closed) causal graph:
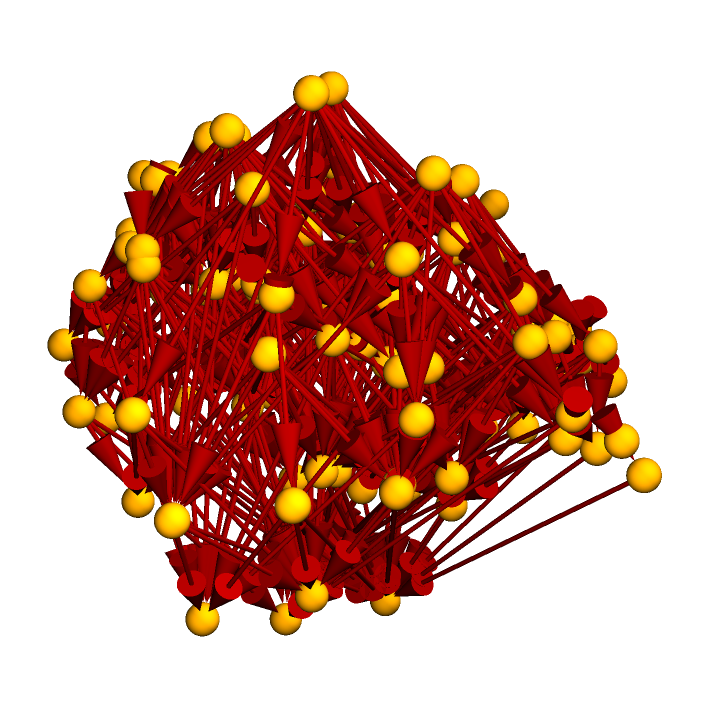
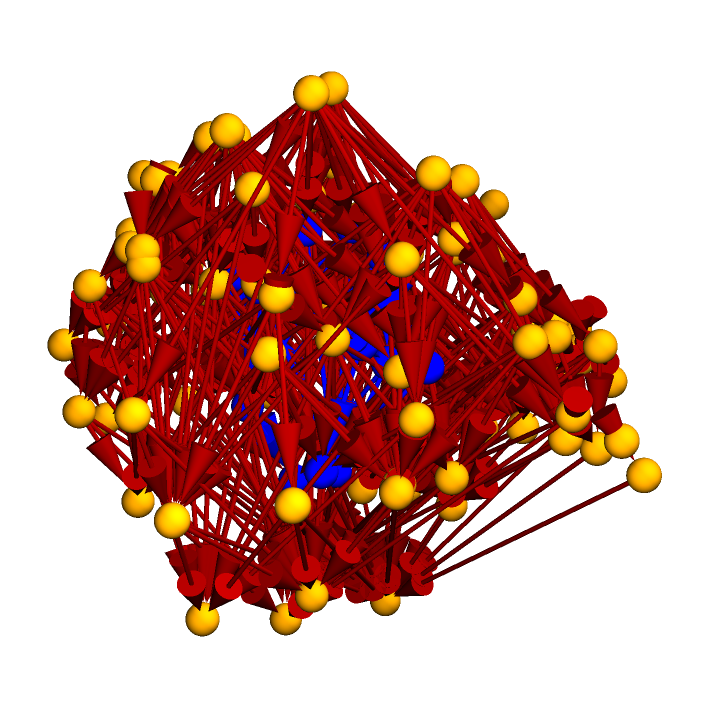
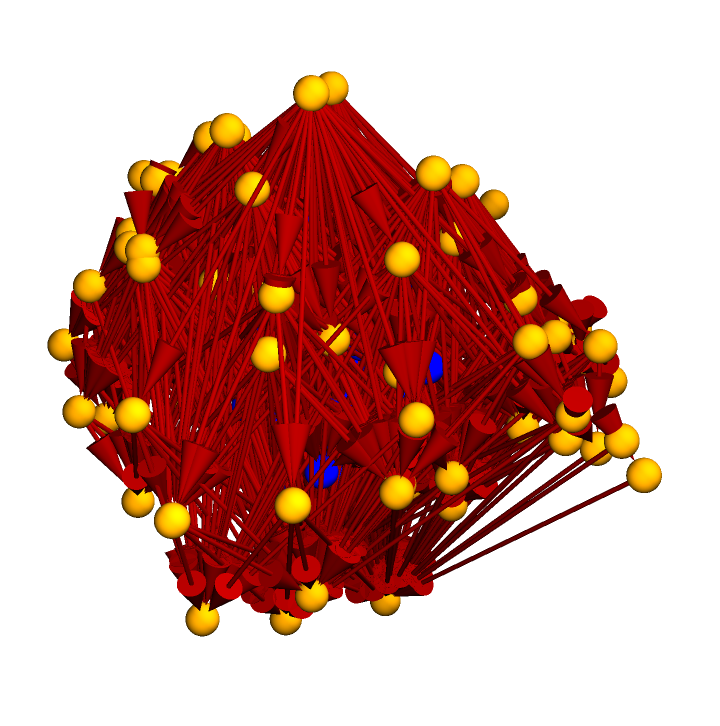
Construct a causal graph by randomly sprinkling 100 points within a diamond-shaped region of 2+1-dimensional Minkowski space:
Construct a subgraph of this causal graph corresponding to a smaller, interior diamond region:
Compute the entanglement entropy associated with this subgraph using the generalized approach:
Highlight the interior subgraph within the larger (transitively reduced) causal graph:
Highlight the interior subgraph within the full (i.e. transitively closed) causal graph:
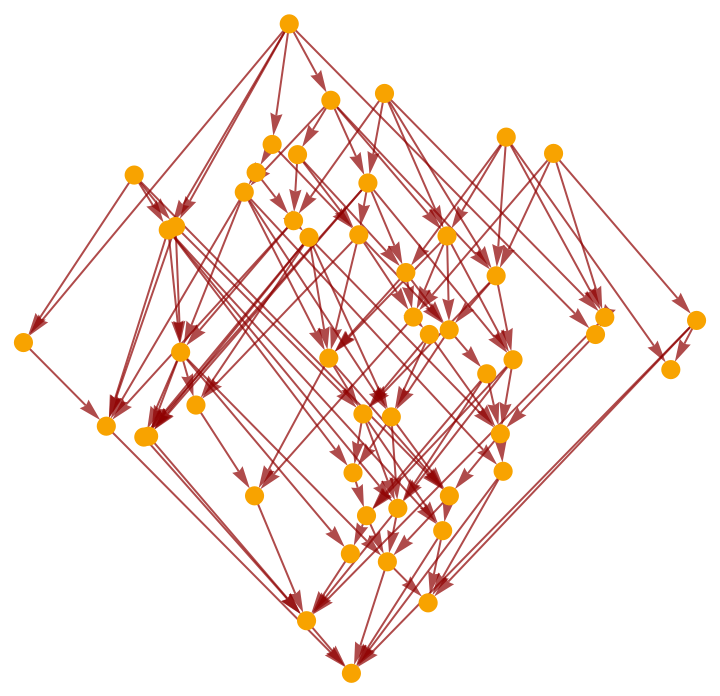
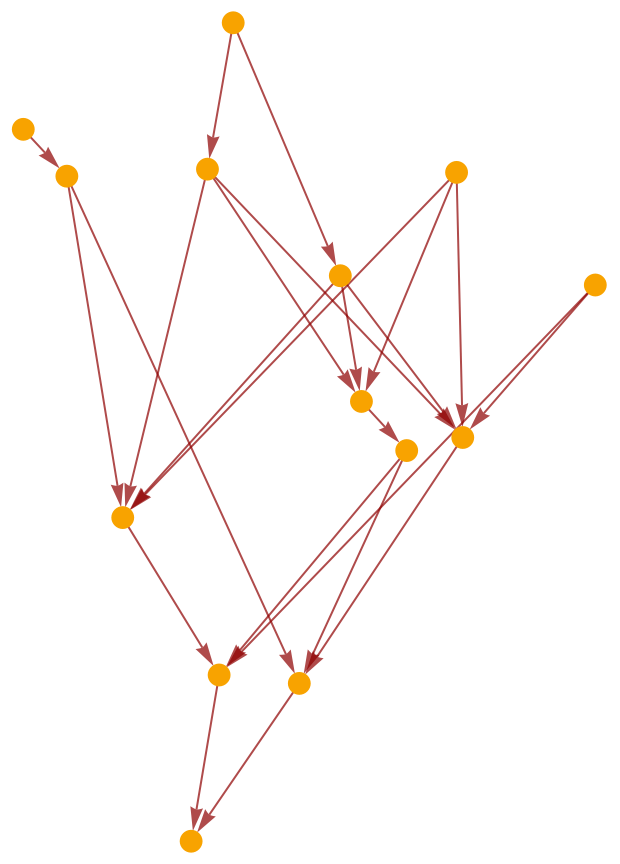
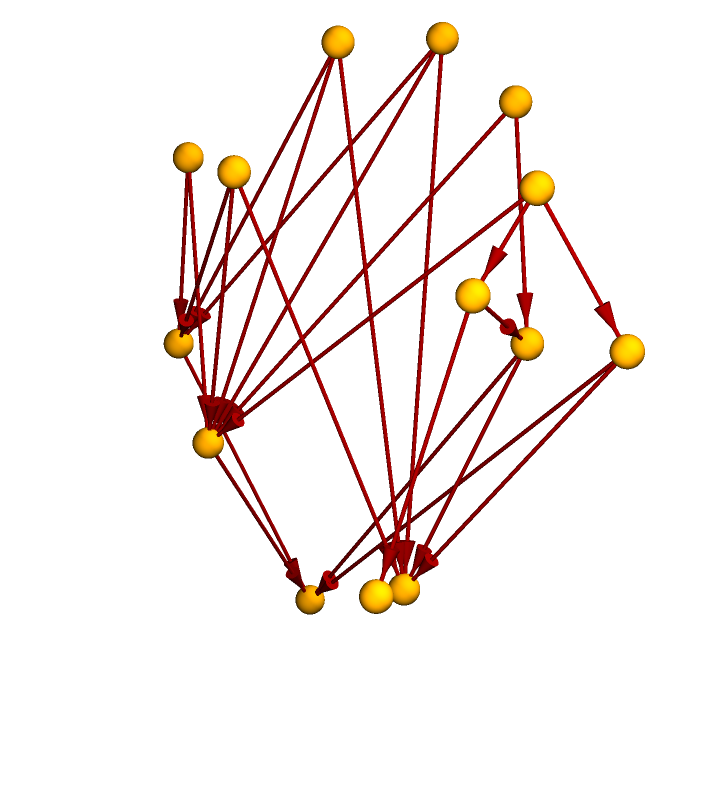
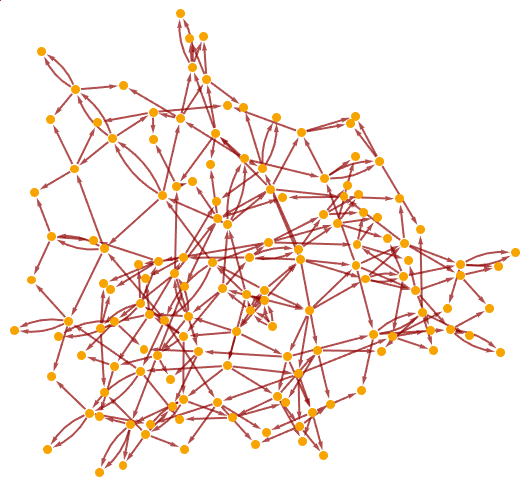
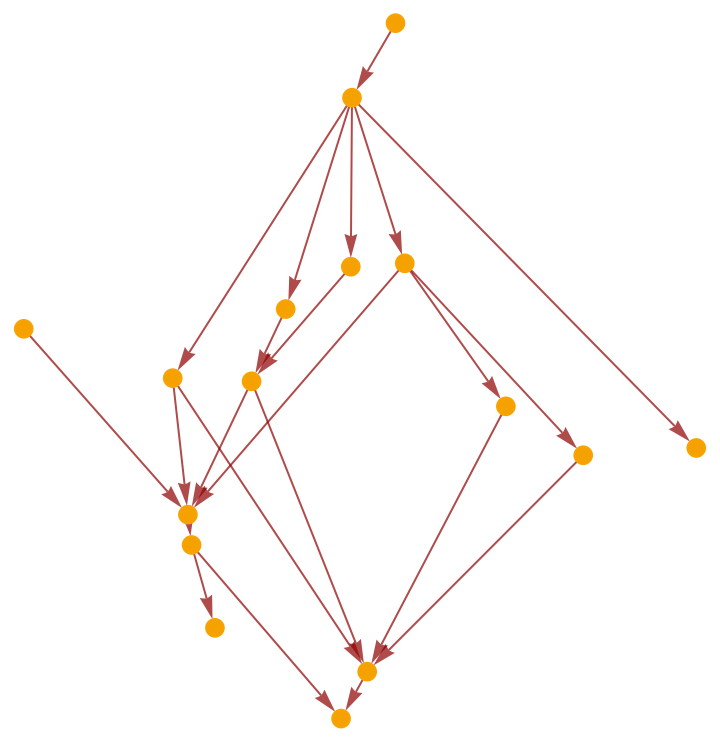
Construct a causal graph by means of a deterministic algorithmic process, e.g. Wolfram model evolution:
Select a random subgraph of the resulting causal graph:
Compute the entanglement entropy associated with this subgraph using the generalized approach (note that when an explicit dimension is not specified, CausalGraphEntanglementEntropyGeneralized will assume that the dimension of the causal graph is equal to 2):
Compute the entanglement entropy associated with this subgraph using the generalized approach, assuming a causal graph dimension of 4 instead (yields an indeterminate result):
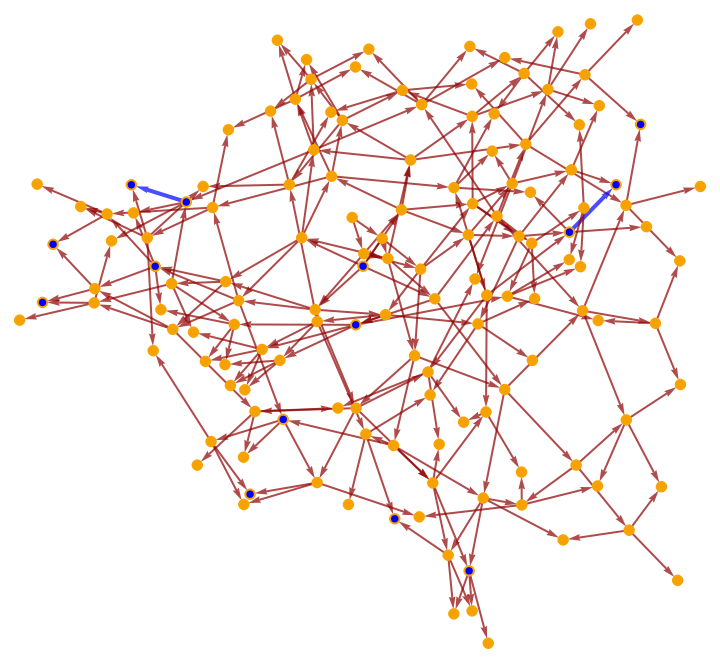
Highlight the interior random subgraph within the larger (transitively reduced) causal graph:
When the generalized eigenvalue problem for the Sorkin–Johnston Wightman function (or, equivalently, the Pauli–Jordan operator) of the corresponding causal set cannot be solved, CausalGraphEntanglementEntropyGeneralized will return Indeterminate:
Highlight the interior subgraph within the larger (transitively reduced) causal graph:
Scope (2)
CausalGraphEntanglementEntropyGeneralized currently supports the computation of causal set Green's functions (and hence entanglement entropies) in 1+1 dimensions:
2+1 dimensions:
And 3+1 dimensions:
When calling CausalGraphEntanglementEntropyGeneralized without any property specified, the property "EntanglementEntropy" is assumed by default:
Render the (transitively reduced) causal graph:
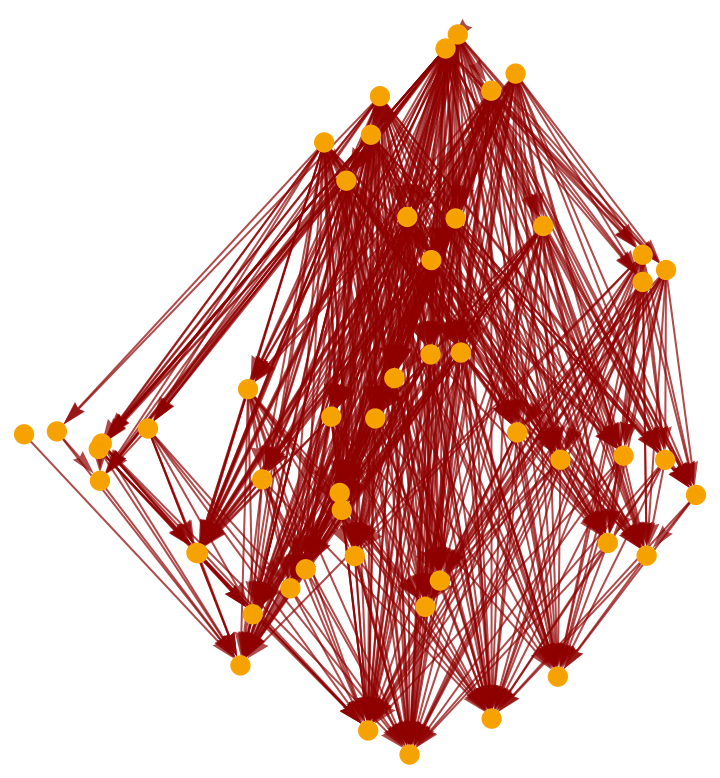
Render the full (i.e. transitively closed) causal graph instead:
Render the (transitively reduced) interior subgraph of the overall causal graph:
Render the full (i.e. transitively closed) interior subgraph of the overall causal graph instead:
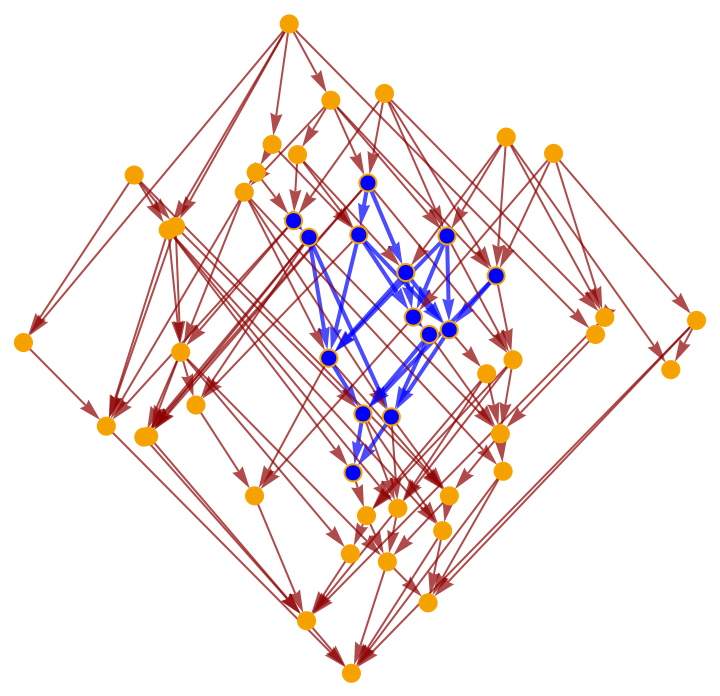
Highlight the interior subgraph within the larger (transitively reduced) causal graph:
Highlight the interior subgraph within the full (i.e. transitively closed) causal graph instead:
![SeedRandom[100];
causalGraph = ResourceFunction["CurvedSpacetimeRegionSprinkling"][
Abs[x] + Abs[y] < N[(Sqrt[0.5]/2)], {x, y}, {{-0.5, 0.5}, {-0.5, 0.5}}, 50]["CausalGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/5c61aab0ccc4a7a2.png)
![subgraph = Subgraph[causalGraph, Select[VertexList[causalGraph], Abs[First[#]] + Abs[Last[#]] < N[(Sqrt[0.125]/2)] &]]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/3a30ed65dad9055e.png)
![SeedRandom[100];
causalGraph = ResourceFunction["CurvedSpacetimeRegionSprinkling"][
Abs[x] + Abs[y] + Abs[z] < N[(Sqrt[0.5]/2)], {x, y, z}, {{-0.5, 0.5}, {-0.5, 0.5}, {-0.5, 0.5}}, 100]["CausalGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/2e40a584161a95a3.png)
![subgraph = Subgraph[causalGraph, Select[VertexList[causalGraph], Abs[#[[1]]] + Abs[#[[2]]] + Abs[#[[3]]] < N[(Sqrt[0.125]/2)] &]]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/53a59dd0095bec50.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/dbca6fd3-7f11-4d33-892d-dde9c923d5db"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/589dbd2fd3060bdf.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/e362666a-ee0c-46c9-8e8c-1d22bf6b0a8d"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/44531b9cae72aab1.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/47947dff-3cd5-40dd-b145-b4c6aef2abeb"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/5efebd50b553f895.png)
![ResourceFunction["CausalGraphEntanglementEntropyGeneralized"][\!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwNlHk8FAgfh2kkUbxRtMorSrYcb7FM6+hXYiNHmlWyEeUq1l1SqzGxIUck
EU1yjWPcDGbG8JsZw7imXCFXIUklFW1bktcfz//fz/P5PF+18wEkzzViYmIe
qxBWOW/hwtB0zAMWfU0owYWNVjepEvWfm5Ewkn3m+0AzfHB5KTLIpYOJQkD4
gN6vmCzs3Fi+qQcUojtlVkhxaCBylZr4nIukHz8lbDtSDbnJlRPqpt0QKbN8
nrk7DUVbJ4jdV3Kx0l1OZDPbg4bPbBocMx9Cls7/lDnhHDTSlimse8UE98HK
1wUXyEDV8pLz06SiFi/FRlWvDMkGPeHHfWmQG+iqtD2sDYu+mMleFlJgXO7w
fEFmEB4aNqJbRwpBQtqWb0QpQae4rPmXGwpBYp6zh1ZwG2hNc/y1PRwcO3GR
pyfIAN6liTFvnXxcnsxkPqX0gJIko9/r+H3UVHcy13iYhxWUIUVR7iNkKzl0
/yPTA19S05TCxWpgzJxAXTkrwLJPE3W6eckw3GrkNetLR+EfJnfYGa2wezS7
fAu5Dk4lpoeNr2SDfbCLW6ZXPfxKbTFmJvMx/seM9nWtQmxZlrA1VWlGFU70
QIJxHSzl1MauOVMGReudKLpXaoFw21Zl/5AQLXI9Jv3a0nCD/7/tx3WFEJ9p
HeDjzAMWdbZk5rcGzO2WxvUfb8PZ4fmWqGIG5loLwut/8MByrF7N26AZ7l/a
neDgQMebzkIry4pGpHjttTp6V4Aq57iBNmkUtDR19p3XE+JspOHx6261KG9f
Mxz2MwM8NloOvLxWiVfcHQxCZjqhPultDOdHLHiLLRyOCEpHjTMee3LN+Oj1
t/ixqrMMaNt8NdH9mgCZGy3mg8q5EKL8DtYGRKBJcPRI4lw9xO5wTHJaYuN/
ae0Zeofywb6LkaBGyYBiUBQ3k27BYSvLhPfm0fjBa5xTO9CCxITe1xUdlaCx
i3C5xomOtR0rPU1XGpF18KSDfoAAdNus5Ezyq6BD45asiEDF2J7Ov3x3O8DS
4uZ0aS4DcqkKo8azbEgvku17iVUg9+LjbFAIF3wVrV+ORnWDp0yy9aATDQ57
laV8ZBWBcPmz2O6xbuw7cIasfTIfKXWbvT+1pKJ1p6xGpuJj3EzRf5dUT0U5
P+2pPp9CvH3d4LVcSSNSnXeu6I9lQHqhjuWOnCpoG8XFoCgW3H2lkxfGKYIX
6isXdeKawTngCJVUwkAFpdSW1ooUPJHUdtB5pQg19n47MvgmHsfO6Xhbuldi
ktaLATVrAZCeGmlnhzLwTfNNqyTZK1AzZ2a2/ToXzM0VxUnuTPS4eHIkNi4H
5CZ3jjyXbUQXztlh/5BexJkmSZJLMngdXf/m89sAfNQ56VSaWQMZrryWd2M8
CLsn8cTChwu/k+2D/FW48NXLMLa5nY/PnlgE8ncxoEZa9Y/iEy04F+3B2pZz
GDe8/BrQFliFb999xUSze2BKI1r9rdcGW1VoH5hxpTD608GLoh8MDFMachpU
6UJ1HpXGVkrH0i+eim1mqVhkqEqMmL+G/5zMV5eS5OEbNy2qg6QA1hwP0REc
QhQRtfN40xX4Iur++Pr1dyHvWEKMS1E3pATbyzVr+SNlcUm1s+ECRjezK+96
0GGXU/+3qVWP+3ZuSTYNpQNW6lgQyHVY1bpV76pUPXzP6jjRMBiCdsVbdElx
lWgkJyFhalAHiq43Qt6/b0JW9IDNnk90lLLzdz/gWIKp/5K4t5RrYLfazPi0
OR+3RD97vPFLMSwZLJZut4yG/RmhHn7hArDb++dOiW8C7A7aI/HrJhYe/Z7x
7uCxYpSaW7f1rFUeRIl2xGUMCZAuKX9ZSrkIxlOCXlWZMfBWzi8eYmv78Pde
SaK2bTZeeK4eQ1lIRmNN2asmxDIgaXnqtIYV41bVjCdcPS7Y34lwdDLOgXDZ
+0Rn3y6Ym3lLmHGrw5+PlkWY3OThsR9163KyeCgd1RQiNHuA2pJJvaJQPqyj
yS/++a0BZPUvSq2xYiFT5iOXY8eHnvcq1l8n0/CwnsGLQ6WNqFi6qW/Xk2rk
1c9f8IrsQnPykq1bWi4Wx6p71RyogVpHZXuN6Szsthyd2iQSAJ1uAkwFLjKa
QiXkBpNhqOnY5sOUdkxpLf2QadiK+TyLA621gVDkcPmohCsLX5eW33s+QMP4
E5BDf5UJMnpGe8+v9qf3sd/9RHchvm7cNerXdwnvdXVbnhsox43iY7aZqe1w
dcusKs++Cu0WNncwiQU49WxsGMU7UGo2aa1VGQf79Z3spiIDMLVCxWZWqQqN
pwNo1Qq1mHjyb2d7Uj0OnN6+QOcxoaZ+/q34qndK2WPNy2waDo1UXtWdZ6O6
h3+g5r5G5A0+uKGYwEAbG0fXAHI5eHyfZP+HKILrDXYufOtK3OB9yOdIaQxU
vP8t1vssD1SDMtNpBc0gme5K0BN1YJetznNXiXxocu5NvmlTAkbflQqI8TQ4
tkjOSPxUgJ5uG1ImHjWh1TRJxv0IHWymMm/lvOHA4GljTXkfFv4hP0J+RKxG
Vht/dp96NUjWZe71UVj9v0ey7ibbRHBwkeRspJ2L4l9tjgf3lMM/YsTGvwaT
4Nx2gf9e/TKstB5v525qgsA9kYoxwU0w9EE4bBoXBVyL+o0H5PPxwXJDzZ2S
FgwlL7cshdBw67h6l9xjNoao9Ofp57DhQOl+zxQCD7L4fvaq/RQ0vXQv1kRY
ip8iTPKY/HLonfR5sTDahvbtDOs+NgvrBE+32Naxscj146d37VzgJKloXiXy
4ZqLppqtfDMsji6qCUapmKZLjwlic6DVh7zfbF87VCdS+jwb86HLecpzp18L
Lgf3xMUYJmIBIYCwTnF1B7txyPuXB/BX6nnSvWAhzoTrKBv6xmCt2Fg0TUCD
EbMLJT9fo+I2m8/Zl+OFMJT+bPpkdAH0V5UlTkATfp28tvR0/hb82VFtOVdO
w9LwSIP3yq0gHT697SaBDVGec5eylOgY8i1G41R5KbqQI04Vsugo43ap5YNd
AcTf6np4/0kKUG6rhwUSOLDDunbNHRUeTNyIz56zYiIWqjmcLopGS9esZ/4L
tcCMd02wUmpDkwTLB1K951GyPFbT2qACY9sWnJaO3oC5ntphczcuGK9rCFoh
52NTr/N3RyMGfjbAh2YOjfB/6+vd2A==
"], {
SparseArray[
Automatic, {100, 100}, 0, {1, {CompressedData["
1:eJxdz70uQwEYgOEjYvAzGUwVaVhYaUi0exeDtiKxqb+txaCxWZiMEhLt0K0x
HCaxNsw26aSJuACTGHmGLyHe5LmAN1utl2oDSZLsJL8NhqEwwjgTZJhmhnly
5ClQDCXKrLFOlV3qHHBEg2NOOOeSa5q06JByxwNdHnnimRd6vNL/4413Pvjk
i+8wbHSUMTJMMvXPbJhjgcWwFJZDnhVWQ5kKG2yyxTZ7YZ9DGpxyxgVXNGlz
Q8ot93T5AUBOLQw=
"], CompressedData["
1:eJwlkW1vmzAUhTGJQkuVZZabZQ0oU1PRMSmNU7rMsPJSmZAU0AwK4KXLMhra
7/2N+2czmnS/3aNzn3PuZfO2bWRJkv4CSRIjDfzATQcIEwcZ1jJKWG3OnBLA
RbBmAGL6yDh5/2H08eL685fv6Y+fv36/AHY2MrGVZhAONXO+9CK2r0G3d3Mb
Rqz6Y0KfJgBdTo3Z0vE2j9CluSp0UVLua5pDHPMjcPIButAxCZExs5ZOIA5n
tWxabrSO06LadaAfUIr0dktaqg76ZNRHE/fH+mS+bV57ysn0yvaCFc0pkLuC
hxXVUx/idXxsQu76NM3yByiy5epYMy1hUuwPtaKSMD6UvA81vIh5A1FL2R6g
nKporIkS/GidZK2Y0ETuKKf9u/uwauh/0khwYpqXIGCk2zsb6cbNrSVyF2W1
q0+QPh0QDjptfdpXX7gcYUDPM64Mtemc2N7mnLhpxndCKQoS2bxow2og65O7
b/a966221e4ZYMbfIccHon4u3uJHcVbUYBEwIGJPruyVog4123uIs/3hH4Ic
Xuw=
"]}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwNlHk8FAgfh2kkUbxRtMorSrYcb7FM6+hXYiNHmlWyEeUq1l1SqzGxIUck
EU1yjWPcDGbG8JsZw7imXCFXIUklFW1bktcfz//fz/P5PF+18wEkzzViYmIe
qxBWOW/hwtB0zAMWfU0owYWNVjepEvWfm5Ewkn3m+0AzfHB5KTLIpYOJQkD4
gN6vmCzs3Fi+qQcUojtlVkhxaCBylZr4nIukHz8lbDtSDbnJlRPqpt0QKbN8
nrk7DUVbJ4jdV3Kx0l1OZDPbg4bPbBocMx9Cls7/lDnhHDTSlimse8UE98HK
1wUXyEDV8pLz06SiFi/FRlWvDMkGPeHHfWmQG+iqtD2sDYu+mMleFlJgXO7w
fEFmEB4aNqJbRwpBQtqWb0QpQae4rPmXGwpBYp6zh1ZwG2hNc/y1PRwcO3GR
pyfIAN6liTFvnXxcnsxkPqX0gJIko9/r+H3UVHcy13iYhxWUIUVR7iNkKzl0
/yPTA19S05TCxWpgzJxAXTkrwLJPE3W6eckw3GrkNetLR+EfJnfYGa2wezS7
fAu5Dk4lpoeNr2SDfbCLW6ZXPfxKbTFmJvMx/seM9nWtQmxZlrA1VWlGFU70
QIJxHSzl1MauOVMGReudKLpXaoFw21Zl/5AQLXI9Jv3a0nCD/7/tx3WFEJ9p
HeDjzAMWdbZk5rcGzO2WxvUfb8PZ4fmWqGIG5loLwut/8MByrF7N26AZ7l/a
neDgQMebzkIry4pGpHjttTp6V4Aq57iBNmkUtDR19p3XE+JspOHx6261KG9f
Mxz2MwM8NloOvLxWiVfcHQxCZjqhPultDOdHLHiLLRyOCEpHjTMee3LN+Oj1
t/ixqrMMaNt8NdH9mgCZGy3mg8q5EKL8DtYGRKBJcPRI4lw9xO5wTHJaYuN/
ae0Zeofywb6LkaBGyYBiUBQ3k27BYSvLhPfm0fjBa5xTO9CCxITe1xUdlaCx
i3C5xomOtR0rPU1XGpF18KSDfoAAdNus5Ezyq6BD45asiEDF2J7Ov3x3O8DS
4uZ0aS4DcqkKo8azbEgvku17iVUg9+LjbFAIF3wVrV+ORnWDp0yy9aATDQ57
laV8ZBWBcPmz2O6xbuw7cIasfTIfKXWbvT+1pKJ1p6xGpuJj3EzRf5dUT0U5
P+2pPp9CvH3d4LVcSSNSnXeu6I9lQHqhjuWOnCpoG8XFoCgW3H2lkxfGKYIX
6isXdeKawTngCJVUwkAFpdSW1ooUPJHUdtB5pQg19n47MvgmHsfO6Xhbuldi
ktaLATVrAZCeGmlnhzLwTfNNqyTZK1AzZ2a2/ToXzM0VxUnuTPS4eHIkNi4H
5CZ3jjyXbUQXztlh/5BexJkmSZJLMngdXf/m89sAfNQ56VSaWQMZrryWd2M8
CLsn8cTChwu/k+2D/FW48NXLMLa5nY/PnlgE8ncxoEZa9Y/iEy04F+3B2pZz
GDe8/BrQFliFb999xUSze2BKI1r9rdcGW1VoH5hxpTD608GLoh8MDFMachpU
6UJ1HpXGVkrH0i+eim1mqVhkqEqMmL+G/5zMV5eS5OEbNy2qg6QA1hwP0REc
QhQRtfN40xX4Iur++Pr1dyHvWEKMS1E3pATbyzVr+SNlcUm1s+ECRjezK+96
0GGXU/+3qVWP+3ZuSTYNpQNW6lgQyHVY1bpV76pUPXzP6jjRMBiCdsVbdElx
lWgkJyFhalAHiq43Qt6/b0JW9IDNnk90lLLzdz/gWIKp/5K4t5RrYLfazPi0
OR+3RD97vPFLMSwZLJZut4yG/RmhHn7hArDb++dOiW8C7A7aI/HrJhYe/Z7x
7uCxYpSaW7f1rFUeRIl2xGUMCZAuKX9ZSrkIxlOCXlWZMfBWzi8eYmv78Pde
SaK2bTZeeK4eQ1lIRmNN2asmxDIgaXnqtIYV41bVjCdcPS7Y34lwdDLOgXDZ
+0Rn3y6Ym3lLmHGrw5+PlkWY3OThsR9163KyeCgd1RQiNHuA2pJJvaJQPqyj
yS/++a0BZPUvSq2xYiFT5iOXY8eHnvcq1l8n0/CwnsGLQ6WNqFi6qW/Xk2rk
1c9f8IrsQnPykq1bWi4Wx6p71RyogVpHZXuN6Szsthyd2iQSAJ1uAkwFLjKa
QiXkBpNhqOnY5sOUdkxpLf2QadiK+TyLA621gVDkcPmohCsLX5eW33s+QMP4
E5BDf5UJMnpGe8+v9qf3sd/9RHchvm7cNerXdwnvdXVbnhsox43iY7aZqe1w
dcusKs++Cu0WNncwiQU49WxsGMU7UGo2aa1VGQf79Z3spiIDMLVCxWZWqQqN
pwNo1Qq1mHjyb2d7Uj0OnN6+QOcxoaZ+/q34qndK2WPNy2waDo1UXtWdZ6O6
h3+g5r5G5A0+uKGYwEAbG0fXAHI5eHyfZP+HKILrDXYufOtK3OB9yOdIaQxU
vP8t1vssD1SDMtNpBc0gme5K0BN1YJetznNXiXxocu5NvmlTAkbflQqI8TQ4
tkjOSPxUgJ5uG1ImHjWh1TRJxv0IHWymMm/lvOHA4GljTXkfFv4hP0J+RKxG
Vht/dp96NUjWZe71UVj9v0ey7ibbRHBwkeRspJ2L4l9tjgf3lMM/YsTGvwaT
4Nx2gf9e/TKstB5v525qgsA9kYoxwU0w9EE4bBoXBVyL+o0H5PPxwXJDzZ2S
FgwlL7cshdBw67h6l9xjNoao9Ofp57DhQOl+zxQCD7L4fvaq/RQ0vXQv1kRY
ip8iTPKY/HLonfR5sTDahvbtDOs+NgvrBE+32Naxscj146d37VzgJKloXiXy
4ZqLppqtfDMsji6qCUapmKZLjwlic6DVh7zfbF87VCdS+jwb86HLecpzp18L
Lgf3xMUYJmIBIYCwTnF1B7txyPuXB/BX6nnSvWAhzoTrKBv6xmCt2Fg0TUCD
EbMLJT9fo+I2m8/Zl+OFMJT+bPpkdAH0V5UlTkATfp28tvR0/hb82VFtOVdO
w9LwSIP3yq0gHT697SaBDVGec5eylOgY8i1G41R5KbqQI04Vsugo43ap5YNd
AcTf6np4/0kKUG6rhwUSOLDDunbNHRUeTNyIz56zYiIWqjmcLopGS9esZ/4L
tcCMd02wUmpDkwTLB1K951GyPFbT2qACY9sWnJaO3oC5ntphczcuGK9rCFoh
52NTr/N3RyMGfjbAh2YOjfB/6+vd2A==
"]}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJwNlHk8FAgfh2kkUbxRtMorSrYcb7FM6+hXYiNHmlWyEeUq1l1SqzGxIUck
EU1yjWPcDGbG8JsZw7imXCFXIUklFW1bktcfz//fz/P5PF+18wEkzzViYmIe
qxBWOW/hwtB0zAMWfU0owYWNVjepEvWfm5Ewkn3m+0AzfHB5KTLIpYOJQkD4
gN6vmCzs3Fi+qQcUojtlVkhxaCBylZr4nIukHz8lbDtSDbnJlRPqpt0QKbN8
nrk7DUVbJ4jdV3Kx0l1OZDPbg4bPbBocMx9Cls7/lDnhHDTSlimse8UE98HK
1wUXyEDV8pLz06SiFi/FRlWvDMkGPeHHfWmQG+iqtD2sDYu+mMleFlJgXO7w
fEFmEB4aNqJbRwpBQtqWb0QpQae4rPmXGwpBYp6zh1ZwG2hNc/y1PRwcO3GR
pyfIAN6liTFvnXxcnsxkPqX0gJIko9/r+H3UVHcy13iYhxWUIUVR7iNkKzl0
/yPTA19S05TCxWpgzJxAXTkrwLJPE3W6eckw3GrkNetLR+EfJnfYGa2wezS7
fAu5Dk4lpoeNr2SDfbCLW6ZXPfxKbTFmJvMx/seM9nWtQmxZlrA1VWlGFU70
QIJxHSzl1MauOVMGReudKLpXaoFw21Zl/5AQLXI9Jv3a0nCD/7/tx3WFEJ9p
HeDjzAMWdbZk5rcGzO2WxvUfb8PZ4fmWqGIG5loLwut/8MByrF7N26AZ7l/a
neDgQMebzkIry4pGpHjttTp6V4Aq57iBNmkUtDR19p3XE+JspOHx6261KG9f
Mxz2MwM8NloOvLxWiVfcHQxCZjqhPultDOdHLHiLLRyOCEpHjTMee3LN+Oj1
t/ixqrMMaNt8NdH9mgCZGy3mg8q5EKL8DtYGRKBJcPRI4lw9xO5wTHJaYuN/
ae0Zeofywb6LkaBGyYBiUBQ3k27BYSvLhPfm0fjBa5xTO9CCxITe1xUdlaCx
i3C5xomOtR0rPU1XGpF18KSDfoAAdNus5Ezyq6BD45asiEDF2J7Ov3x3O8DS
4uZ0aS4DcqkKo8azbEgvku17iVUg9+LjbFAIF3wVrV+ORnWDp0yy9aATDQ57
laV8ZBWBcPmz2O6xbuw7cIasfTIfKXWbvT+1pKJ1p6xGpuJj3EzRf5dUT0U5
P+2pPp9CvH3d4LVcSSNSnXeu6I9lQHqhjuWOnCpoG8XFoCgW3H2lkxfGKYIX
6isXdeKawTngCJVUwkAFpdSW1ooUPJHUdtB5pQg19n47MvgmHsfO6Xhbuldi
ktaLATVrAZCeGmlnhzLwTfNNqyTZK1AzZ2a2/ToXzM0VxUnuTPS4eHIkNi4H
5CZ3jjyXbUQXztlh/5BexJkmSZJLMngdXf/m89sAfNQ56VSaWQMZrryWd2M8
CLsn8cTChwu/k+2D/FW48NXLMLa5nY/PnlgE8ncxoEZa9Y/iEy04F+3B2pZz
GDe8/BrQFliFb999xUSze2BKI1r9rdcGW1VoH5hxpTD608GLoh8MDFMachpU
6UJ1HpXGVkrH0i+eim1mqVhkqEqMmL+G/5zMV5eS5OEbNy2qg6QA1hwP0REc
QhQRtfN40xX4Iur++Pr1dyHvWEKMS1E3pATbyzVr+SNlcUm1s+ECRjezK+96
0GGXU/+3qVWP+3ZuSTYNpQNW6lgQyHVY1bpV76pUPXzP6jjRMBiCdsVbdElx
lWgkJyFhalAHiq43Qt6/b0JW9IDNnk90lLLzdz/gWIKp/5K4t5RrYLfazPi0
OR+3RD97vPFLMSwZLJZut4yG/RmhHn7hArDb++dOiW8C7A7aI/HrJhYe/Z7x
7uCxYpSaW7f1rFUeRIl2xGUMCZAuKX9ZSrkIxlOCXlWZMfBWzi8eYmv78Pde
SaK2bTZeeK4eQ1lIRmNN2asmxDIgaXnqtIYV41bVjCdcPS7Y34lwdDLOgXDZ
+0Rn3y6Ym3lLmHGrw5+PlkWY3OThsR9163KyeCgd1RQiNHuA2pJJvaJQPqyj
yS/++a0BZPUvSq2xYiFT5iOXY8eHnvcq1l8n0/CwnsGLQ6WNqFi6qW/Xk2rk
1c9f8IrsQnPykq1bWi4Wx6p71RyogVpHZXuN6Szsthyd2iQSAJ1uAkwFLjKa
QiXkBpNhqOnY5sOUdkxpLf2QadiK+TyLA621gVDkcPmohCsLX5eW33s+QMP4
E5BDf5UJMnpGe8+v9qf3sd/9RHchvm7cNerXdwnvdXVbnhsox43iY7aZqe1w
dcusKs++Cu0WNncwiQU49WxsGMU7UGo2aa1VGQf79Z3spiIDMLVCxWZWqQqN
pwNo1Qq1mHjyb2d7Uj0OnN6+QOcxoaZ+/q34qndK2WPNy2waDo1UXtWdZ6O6
h3+g5r5G5A0+uKGYwEAbG0fXAHI5eHyfZP+HKILrDXYufOtK3OB9yOdIaQxU
vP8t1vssD1SDMtNpBc0gme5K0BN1YJetznNXiXxocu5NvmlTAkbflQqI8TQ4
tkjOSPxUgJ5uG1ImHjWh1TRJxv0IHWymMm/lvOHA4GljTXkfFv4hP0J+RKxG
Vht/dp96NUjWZe71UVj9v0ey7ibbRHBwkeRspJ2L4l9tjgf3lMM/YsTGvwaT
4Nx2gf9e/TKstB5v525qgsA9kYoxwU0w9EE4bBoXBVyL+o0H5PPxwXJDzZ2S
FgwlL7cshdBw67h6l9xjNoao9Ofp57DhQOl+zxQCD7L4fvaq/RQ0vXQv1kRY
ip8iTPKY/HLonfR5sTDahvbtDOs+NgvrBE+32Naxscj146d37VzgJKloXiXy
4ZqLppqtfDMsji6qCUapmKZLjwlic6DVh7zfbF87VCdS+jwb86HLecpzp18L
Lgf3xMUYJmIBIYCwTnF1B7txyPuXB/BX6nnSvWAhzoTrKBv6xmCt2Fg0TUCD
EbMLJT9fo+I2m8/Zl+OFMJT+bPpkdAH0V5UlTkATfp28tvR0/hb82VFtOVdO
w9LwSIP3yq0gHT697SaBDVGec5eylOgY8i1G41R5KbqQI04Vsugo43ap5YNd
AcTf6np4/0kKUG6rhwUSOLDDunbNHRUeTNyIz56zYiIWqjmcLopGS9esZ/4L
tcCMd02wUmpDkwTLB1K951GyPFbT2qACY9sWnJaO3oC5ntphczcuGK9rCFoh
52NTr/N3RyMGfjbAh2YOjfB/6+vd2A==
"], {
{Hue[0, 1, 0.56], Arrowheads[0.046553254371331225`], Arrow3DBox[TubeBox[CompressedData["
1:eJwVxVmbqQwAAGAZj2hCacRYakZSx9YoKSfLKWUmUtaQyNL99xu/f3ae8968
n4//No9oJBL5H4hE/h3NRMfRSWwYW8QzcSzOxaX4AMRAGuRBETTAOWiDQYJN
tBKDxC4JJNHkV3KSnCVtCIBQiIM06AeyIfdVghEYh/NwAX6H6zAD/4J/wwt4
CR9gD/bhZwpI2enXdD7Nprk0n16knQyKoEgOKSEs0kFEZIQYiI2ckSALZGPZ
eLad7WanWSNrZ/fZK8a+oW/jnJab4wCO4Z94FafxFi7iA3yEf+M/eTQ/zGv5
VQEqlApsoVMwCvPCrnAuBO/a+6qIFrmiWXSL9xJQHpRXlUwFq7xXyhWuIlWm
BEbQRIvgCZEYEBPCIOaETThEQEZJluTJIWmQM9IkF+SW3JPHj5cP9GP8MfnU
qhqFUWWKploUT4mURBnUnLKpoPZSw2pkja4FtTvN0lw9VS/Wy3Wi3qlv6o96
yMQZkEkwVYZiZGbETBid1djVL60BNKKNWINtcA2+YTe2jX3j1Ew10SbXnDXN
5r35aE1bbnvYHre19qLttFedP120O+wu+Ay/EiChKJQEVuAFSTCEubAVzsJF
CHpgD+pJvWnP7F3Enej2U320X+pz/a++2Xf7DxmVMZmWW7IoD2RDnsu2HAy0
gftbUyAFU4pKSaEVXhGVsWIoM2WuOMpWOSsXJRhKI200V6PqiwqqSTWlCqqi
TtW9+phqOqbTekvndVEf6IZu644eGJyhGavvnQmYE9NeSFbMiluvVt4qW7TV
troWb00tw7KtrbWz9tbRCpaJJbYsL6tOxpFW7hpYv6zR9dd6sp5tSpveZrxx
NtvNeXPfotvJTtu/7Z29ewAPuUPpUD10DtJBPowO38e3o3QanhYn5+Sejl7C
w7yy9+lVPdrjPdGTvJFneN+e7QVnwI/6ZZ/wBb/vy77iD/2Rr/sbf+8f/dsF
uHAX++Je01fsOriOAyDgAi34CdwbdqNv/G18M27mzbltb8EduH/dJ3f7ATzj
T/CZeBJP6ik/9RAMoTAXlkI5HIV/QjN0wnN4+QtmdbhM
"]], 0.01435649591870683]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], SphereBox[1, 0.01435649591870683], SphereBox[2, 0.01435649591870683], SphereBox[3, 0.01435649591870683], SphereBox[4, 0.01435649591870683], SphereBox[5, 0.01435649591870683], SphereBox[6, 0.01435649591870683], SphereBox[7, 0.01435649591870683], SphereBox[8, 0.01435649591870683], SphereBox[9, 0.01435649591870683], SphereBox[10, 0.01435649591870683], SphereBox[11, 0.01435649591870683], SphereBox[12, 0.01435649591870683], SphereBox[13, 0.01435649591870683], SphereBox[14, 0.01435649591870683], SphereBox[15, 0.01435649591870683], SphereBox[16, 0.01435649591870683], SphereBox[17, 0.01435649591870683], SphereBox[18, 0.01435649591870683], SphereBox[19, 0.01435649591870683], SphereBox[20, 0.01435649591870683], SphereBox[21, 0.01435649591870683], SphereBox[22, 0.01435649591870683], SphereBox[23, 0.01435649591870683], SphereBox[24, 0.01435649591870683], SphereBox[25, 0.01435649591870683], SphereBox[26, 0.01435649591870683], SphereBox[27, 0.01435649591870683], SphereBox[28, 0.01435649591870683], SphereBox[29, 0.01435649591870683], SphereBox[30, 0.01435649591870683], SphereBox[31, 0.01435649591870683], SphereBox[32, 0.01435649591870683], SphereBox[33, 0.01435649591870683], SphereBox[34, 0.01435649591870683], SphereBox[35, 0.01435649591870683], SphereBox[36, 0.01435649591870683], SphereBox[37, 0.01435649591870683], SphereBox[38, 0.01435649591870683], SphereBox[39, 0.01435649591870683], SphereBox[40, 0.01435649591870683], SphereBox[41, 0.01435649591870683], SphereBox[42, 0.01435649591870683], SphereBox[43, 0.01435649591870683], SphereBox[44, 0.01435649591870683], SphereBox[45, 0.01435649591870683], SphereBox[46, 0.01435649591870683], SphereBox[47, 0.01435649591870683], SphereBox[48, 0.01435649591870683], SphereBox[49, 0.01435649591870683], SphereBox[50, 0.01435649591870683], SphereBox[51, 0.01435649591870683], SphereBox[52, 0.01435649591870683], SphereBox[53, 0.01435649591870683], SphereBox[54, 0.01435649591870683], SphereBox[55, 0.01435649591870683], SphereBox[56, 0.01435649591870683], SphereBox[57, 0.01435649591870683], SphereBox[58, 0.01435649591870683], SphereBox[59, 0.01435649591870683], SphereBox[60, 0.01435649591870683], SphereBox[61, 0.01435649591870683], SphereBox[62, 0.01435649591870683], SphereBox[63, 0.01435649591870683], SphereBox[64, 0.01435649591870683], SphereBox[65, 0.01435649591870683], SphereBox[66, 0.01435649591870683], SphereBox[67, 0.01435649591870683], SphereBox[68, 0.01435649591870683], SphereBox[69, 0.01435649591870683], SphereBox[70, 0.01435649591870683], SphereBox[71, 0.01435649591870683], SphereBox[72, 0.01435649591870683], SphereBox[73, 0.01435649591870683], SphereBox[74, 0.01435649591870683], SphereBox[75, 0.01435649591870683], SphereBox[76, 0.01435649591870683], SphereBox[77, 0.01435649591870683], SphereBox[78, 0.01435649591870683], SphereBox[79, 0.01435649591870683], SphereBox[80, 0.01435649591870683], SphereBox[81, 0.01435649591870683], SphereBox[82, 0.01435649591870683], SphereBox[83, 0.01435649591870683], SphereBox[84, 0.01435649591870683], SphereBox[85, 0.01435649591870683], SphereBox[86, 0.01435649591870683], SphereBox[87, 0.01435649591870683], SphereBox[88, 0.01435649591870683], SphereBox[89, 0.01435649591870683], SphereBox[90, 0.01435649591870683], SphereBox[91, 0.01435649591870683], SphereBox[92, 0.01435649591870683], SphereBox[93, 0.01435649591870683], SphereBox[94, 0.01435649591870683], SphereBox[95, 0.01435649591870683], SphereBox[96, 0.01435649591870683], SphereBox[97, 0.01435649591870683], SphereBox[98, 0.01435649591870683], SphereBox[99, 0.01435649591870683], SphereBox[100, 0.01435649591870683]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
Boxed->False,
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}}]\), \!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBSQG2/iFib1JlAgAAAA0AAAADAAAAnCtmD20nnL8rwZJMHzKtv3410XxP
a6U/BO+8KaWmjj+lvu3CBdG8v91RacEyxJk/yiWJDs0DnL+I0ct7ayZUP/v0
FJcKwLQ/XG9DnFKrtL8TF5TFxq+Sv1GPyD5c/6i/rPdlFshClL+oNh83f+96
v/ZVpCIIBsG/gPT7H8u7aL+Gw7qwk2SqPyRZ1Prjq7S//J7KUbvXc79OqRUu
UoqwvzoPBAQ9NbY/6Kyuld/Wpb+LUT+hquaaPwsyOipiv7E/MvHUY1HQp7/o
vSTcbdN0v5XM0Ehh1q6/cCmCFodyvj/Y8MfaPYqDP8BFtw04EqS/2JfZ5VWG
pj/Usa2N4T++v/nievvV74k/g2XtdJ4Xqr9z+oclVq6sv11+f1anuaq/C2B0
xfBOpj+LicydmM+SP4COInhwA7w/KEuoqw==
"], {
SparseArray[
Automatic, {13, 13}, 0, {1, {{0, 4, 5, 9, 10, 10, 10, 13, 17, 18, 18, 19, 20, 25}, {{4}, {6}, {9}, {12}, {5}, {4}, {6}, {9}, {12}, {
5}, {1}, {2}, {11}, {4}, {6}, {9}, {12}, {5}, {5}, {5}, {
4}, {6}, {9}, {10}, {12}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}, VertexCoordinates -> CompressedData["
1:eJwBSQG2/iFib1JlAgAAAA0AAAADAAAAnCtmD20nnL8rwZJMHzKtv3410XxP
a6U/BO+8KaWmjj+lvu3CBdG8v91RacEyxJk/yiWJDs0DnL+I0ct7ayZUP/v0
FJcKwLQ/XG9DnFKrtL8TF5TFxq+Sv1GPyD5c/6i/rPdlFshClL+oNh83f+96
v/ZVpCIIBsG/gPT7H8u7aL+Gw7qwk2SqPyRZ1Prjq7S//J7KUbvXc79OqRUu
UoqwvzoPBAQ9NbY/6Kyuld/Wpb+LUT+hquaaPwsyOipiv7E/MvHUY1HQp7/o
vSTcbdN0v5XM0Ehh1q6/cCmCFodyvj/Y8MfaPYqDP8BFtw04EqS/2JfZ5VWG
pj/Usa2N4T++v/nievvV74k/g2XtdJ4Xqr9z+oclVq6sv11+f1anuaq/C2B0
xfBOpj+LicydmM+SP4COInhwA7w/KEuoqw==
"]}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJwBSQG2/iFib1JlAgAAAA0AAAADAAAAnCtmD20nnL8rwZJMHzKtv3410XxP
a6U/BO+8KaWmjj+lvu3CBdG8v91RacEyxJk/yiWJDs0DnL+I0ct7ayZUP/v0
FJcKwLQ/XG9DnFKrtL8TF5TFxq+Sv1GPyD5c/6i/rPdlFshClL+oNh83f+96
v/ZVpCIIBsG/gPT7H8u7aL+Gw7qwk2SqPyRZ1Prjq7S//J7KUbvXc79OqRUu
UoqwvzoPBAQ9NbY/6Kyuld/Wpb+LUT+hquaaPwsyOipiv7E/MvHUY1HQp7/o
vSTcbdN0v5XM0Ehh1q6/cCmCFodyvj/Y8MfaPYqDP8BFtw04EqS/2JfZ5VWG
pj/Usa2N4T++v/nievvV74k/g2XtdJ4Xqr9z+oclVq6sv11+f1anuaq/C2B0
xfBOpj+LicydmM+SP4COInhwA7w/KEuoqw==
"], {
{Hue[0, 1, 0.56], Arrowheads[Medium], Arrow3DBox[TubeBox[{1, 4}], 0.00617211644877777], Arrow3DBox[TubeBox[{1, 6}], 0.00617211644877777], Arrow3DBox[TubeBox[{1, 9}], 0.00617211644877777], Arrow3DBox[TubeBox[{1, 12}], 0.00617211644877777], Arrow3DBox[TubeBox[{2, 5}], 0.00617211644877777], Arrow3DBox[TubeBox[{3, 4}], 0.00617211644877777], Arrow3DBox[TubeBox[{3, 6}], 0.00617211644877777], Arrow3DBox[TubeBox[{3, 9}], 0.00617211644877777], Arrow3DBox[TubeBox[{3, 12}], 0.00617211644877777], Arrow3DBox[TubeBox[{4, 5}], 0.00617211644877777], Arrow3DBox[TubeBox[{7, 1}], 0.00617211644877777], Arrow3DBox[TubeBox[{7, 2}], 0.00617211644877777], Arrow3DBox[TubeBox[{7, 11}], 0.00617211644877777], Arrow3DBox[TubeBox[{8, 4}], 0.00617211644877777], Arrow3DBox[TubeBox[{8, 6}], 0.00617211644877777], Arrow3DBox[TubeBox[{8, 9}], 0.00617211644877777], Arrow3DBox[TubeBox[{8, 12}], 0.00617211644877777], Arrow3DBox[TubeBox[{9, 5}], 0.00617211644877777], Arrow3DBox[TubeBox[{11, 5}], 0.00617211644877777], Arrow3DBox[TubeBox[{12, 5}], 0.00617211644877777], Arrow3DBox[TubeBox[{13, 4}], 0.00617211644877777], Arrow3DBox[TubeBox[{13, 6}], 0.00617211644877777], Arrow3DBox[TubeBox[{13, 9}], 0.00617211644877777], Arrow3DBox[TubeBox[{13, 10}], 0.00617211644877777], Arrow3DBox[TubeBox[{13, 12}], 0.00617211644877777]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], SphereBox[1, 0.00617211644877777], SphereBox[2, 0.00617211644877777], SphereBox[3, 0.00617211644877777], SphereBox[4, 0.00617211644877777], SphereBox[5, 0.00617211644877777], SphereBox[6, 0.00617211644877777], SphereBox[7, 0.00617211644877777], SphereBox[8, 0.00617211644877777], SphereBox[9, 0.00617211644877777], SphereBox[10, 0.00617211644877777], SphereBox[11, 0.00617211644877777], SphereBox[12, 0.00617211644877777], SphereBox[13, 0.00617211644877777]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
Boxed->False,
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}}]\), 3]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/501a179880ba3a2b.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/069d575d-cb80-40c1-bf9d-680038bc5ae6"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/10115c3007750e24.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/8fdb3560-3bb3-48aa-9fec-7795e9cf4261"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/4782e7236f82e62e.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/7a9c1699-4687-447c-94a4-97b0a6c5546f"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/62dfdc321f237f14.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/efc0c97a-d038-4697-8046-e51c436da8d1"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/749647d3bdeb0442.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/70a4026c-6a7e-490c-a3f1-1a038805843c"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/7484e9d32b5263f6.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/20b45782-3ca4-4037-8cf2-7d91e812d664"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/67381db39b4dbdbd.png)

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/d78ae3f3-2726-460f-99a6-c90c3e625c60"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/1f66ef7922adb560.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/4a912d9e-8a65-499a-8bed-b2b3272b953a"]](https://www.wolframcloud.com/obj/resourcesystem/images/c98/c980dbae-d927-43e9-8245-3505fd89cee3/3b861876bbe872bc.png)