Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 CarlemanMatrix

Source Notebook

Evaluate the Carleman matrix of a function

Contributed by: Jan Mangaldan

ResourceFunction["CarlemanMatrix"][f,{x,x0,{m,n}}]

gives the order {m,n} Carleman matrix of f about the point x=x0.

ResourceFunction["CarlemanMatrix"][f,{x,x0,n}]

gives the order n Carleman matrix of f about the point x=x0.

Details

The Carleman matrix of an infinitely differentiable function f(x) has elements .
The Carleman matrix about the point x=x0 is defined only when there is a corresponding power series at that point.
The order {m,n} Carleman matrix has dimensions (m+1)×(n+1).

Examples

Basic Examples (1) 

A Carleman matrix of order {2,3} for Exp[x]:

In[1]:=
ResourceFunction["CarlemanMatrix"][ Exp[x], {x, 0, {2, 3}}] // MatrixForm
Out[1]=

Scope (2) 

Carleman matrix of an arbitrary function:

In[2]:=
ResourceFunction["CarlemanMatrix"][f[x], {x, 0, 2}] // MatrixForm
Out[2]=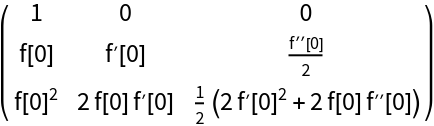

Carleman matrix with a complex-valued expansion point:

In[3]:=
ResourceFunction["CarlemanMatrix"][Cos[x], {x, I, 3}] // MatrixForm
Out[3]=

Properties and Relations (3) 

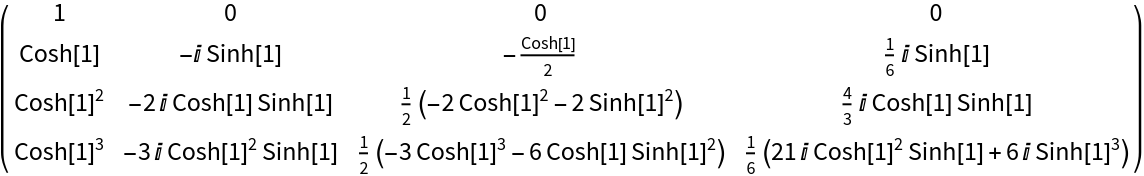The kth row of the Carleman matrix of f(x) corresponds to the power series coefficients of :

In[4]:=
ResourceFunction["CarlemanMatrix"][Log[x], {x, 1, 5}][[3]]
Out[4]=
In[5]:=
Table[SeriesCoefficient[Log[x]^(3 - 1), {x, 1, k}], {k, 0, 5}]
Out[5]=

If f(0)=0, the second row of the nth matrix power of the Carleman matrix of f(x) corresponds to the power series coefficients of the nth composition of f(x):

In[6]:=
MatrixPower[ResourceFunction["CarlemanMatrix"][Sin[x], {x, 0, 5}], 4][[2]]
Out[6]=
In[7]:=
CoefficientList[Series[Nest[Sin, x, 4], {x, 0, 5}], x]
Out[7]=

If f(0)=0, the second row of the inverse of the Carleman matrix of f(x) corresponds to the power series coefficients of :

In[8]:=
Inverse[ResourceFunction["CarlemanMatrix"][ Exp[x] - 1, {x, 0, 5}]][[2]]
Out[8]=
In[9]:=
CoefficientList[InverseSeries[Series[Exp[x] - 1, {x, 0, 5}]], x]
Out[9]=

Version History

  • 1.0.0 – 04 March 2021

Related Resources

License Information