Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 CanonicalTilingMask

Source Notebook

Get a canonical form for an overlap tiling mask

Contributed by: Wolfram Research

ResourceFunction["CanonicalTilingMask"][array]

given a mask array, find a canonical form of that mask.

Details

In this code, the mask for is {{0,0,1},{1,1,1}}. Below, the shapes are given instead of the arrays as a visual aid for the reader:
This function is very specific to the overlap tilings seen in the resource function FindMinimalTilings.
A tile mask is a subset of positions within a rectangular array, such as the a values in {{a,a,a},{_,a,_}}. This particular mask is also known as the Tetris T shape, .
The results of FindMinimalTilings on mask has identical results to rotations and reflections of .
The results of running FindMinimalTilings on mask has identical results to mask (skew equivalency).
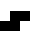
Similarly, and are equivalent masks for overlap tiling systems.
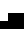
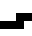
Evaluating ResourceFunction["CanonicalTilingMask"] on any rotation or reflection of masks , or returns .
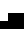
, and are canonical. is the canonical form of . is the canonical form of . is the canonical form of .
Currently, many hours of computer time are needed to run FindMinimalTilings on masks , and . These are all equivalent to . The point of this function is to find these equivalencies before an expensive run.
For overlap tiling systems, these results only meaningfully apply to 2D shapes. The domino array {{1,1}} can be considered a 1D mask.

Examples

Basic Examples (2) 

The canonical tiling mask for is :

In[1]:=
ResourceFunction["CanonicalTilingMask"][{{1, 0}, {1, 1}, {1, 0}}]
Out[1]=

The following mask is canonical:

In[2]:=
mask = {{0, 1, 1, 1, 0}, {1, 0, 0, 0, 1}, {1, 0, 0, 0, 1}, {1, 0, 0, 0, 1}, {0, 1, 1, 1, 0}}; ResourceFunction["CanonicalTilingMask"][mask] === mask
Out[3]=

Scope (1) 

Find canonical masks for the pentomino shapes:

In[4]:=
pentominoes = {{{1, 1, 1, 1, 1}}, {{0, 1, 1}, {1, 1, 1}}, {{1, 0, 1}, {1, 1, 1}}, {{0, 0, 0, 1}, {1, 1, 1, 1}}, {{0, 0, 1, 0}, {1, 1, 1, 1}}, {{0, 0, 1, 1}, {1, 1, 1, 0}}, {{0, 0, 1}, {0, 0, 1}, {1, 1, 1}}, {{0, 0, 1}, {0, 1, 1}, {1, 1, 0}}, {{0, 0, 1}, {1, 1, 1}, {0, 0, 1}}, {{0, 0, 1}, {1, 1, 1}, {0, 1, 0}}, {{0, 0, 1}, {1, 1, 1}, {1, 0, 0}}, {{0, 1, 0}, {1, 1, 1}, {0, 1, 0}}}; Grid[Transpose[ ArrayPlot[#, PixelConstrained -> 4, Frame -> False] & /@ # & /@ SortBy[{#, ResourceFunction["CanonicalTilingMask"][#]} & /@ pentominoes, Last]]]
Out[5]=

Neat Examples (3) 

Find canonical masks (bottom row) for the hexomino shapes (top row):

In[6]:=
hexominoes = {{{1, 1, 1, 1, 1, 1}}, {{1, 1, 1}, {1, 1, 1}}, {{0, 0, 1, 1}, {1, 1, 1, 1}}, {{0, 1, 0, 1}, {1, 1, 1, 1}}, {{0, 1, 1, 0}, { 1, 1, 1, 1}}, {{0, 1, 1, 1}, {1, 1, 0, 1}}, {{0, 1, 1, 1}, {1, 1, 1, 0}}, {{1, 0, 0, 1}, {1, 1, 1, 1}}, {{0, 0, 0, 0, 1}, {1, 1, 1, 1, 1}}, {{0, 0, 0, 1, 0}, {1, 1, 1, 1, 1}}, {{0, 0, 0, 1, 1}, {1, 1, 1, 1, 0}}, {{0, 0, 1, 0, 0}, {1, 1, 1, 1, 1}}, {{0, 0, 1, 1, 1}, {1, 1, 1, 0, 0}}, {{0, 0, 1}, {0, 1, 1}, {1, 1, 1}}, {{0, 0, 1}, {1, 0, 1}, {1, 1, 1}}, {{0, 0, 1}, {1, 1, 1}, {0, 1, 1}}, {{0, 0, 1}, {1, 1, 1}, {1, 0, 1}}, {{0, 0, 1}, {1, 1, 1}, {1, 1, 0}}, {{ 0, 1, 0}, {1, 1, 1}, {0, 1, 1}}, {{0, 1, 0}, {1, 1, 1}, {1, 0, 1}}, {{0, 0, 0, 1}, {0, 0, 0, 1}, {1, 1, 1, 1}}, {{0, 0, 0, 1}, {0, 0, 1, 1}, {1, 1, 1, 0}}, {{0, 0, 0, 1}, {0, 1, 1, 1}, {1, 1, 0, 0}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {0, 0, 0, 1}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {0, 0, 1, 0}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {0, 1, 0, 0}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {1, 0, 0, 0}}, {{0, 0, 1, 0}, {0, 0, 1, 0}, {1, 1, 1, 1}}, {{0, 0, 1, 0}, {0, 0, 1, 1}, {1, 1, 1, 0}}, {{0, 0, 1, 0}, {0, 1, 1, 1}, {1, 1, 0, 0}}, {{0, 0, 1, 0}, {1, 1, 1, 0}, {0, 0, 1, 1}}, {{0, 0, 1, 0}, {1, 1, 1, 1}, {0, 0, 1, 0}}, {{0, 0, 1, 0}, {1, 1, 1, 1}, {0, 1, 0, 0}}, {{0, 0, 1, 1}, {0, 0, 1, 0}, {1, 1, 1, 0}}, {{0, 0, 1, 1}, {0, 1, 1, 0}, {1, 1, 0, 0}}}; Grid[Transpose[ ArrayPlot[#, PixelConstrained -> 4, Frame -> False] & /@ # & /@ SortBy[{#, ResourceFunction["CanonicalTilingMask"][#]} & /@ hexominoes, Last]]]
Out[7]=

Find a canonical mask for a random heptomino:

In[8]:=
heptominoes = {{{1, 1, 1, 1, 1, 1, 1}}, {{0, 1, 1, 1}, {1, 1, 1, 1}}, {{1, 0, 1, 1}, {1, 1, 1, 1}}, {{0, 0, 0, 1, 1}, {1, 1, 1, 1, 1}}, {{0, 0, 1, 0, 1}, {1, 1, 1, 1, 1}}, {{0, 0, 1, 1, 0}, {1, 1, 1, 1, 1}}, {{0, 0, 1, 1, 1}, {1, 1, 1, 0, 1}}, {{0, 0, 1, 1, 1}, { 1, 1, 1, 1, 0}}, {{0, 1, 0, 0, 1}, {1, 1, 1, 1, 1}}, {{0, 1, 0, 1, 0}, {1, 1, 1, 1, 1}}, {{0, 1, 0, 1, 1}, {1, 1, 1, 1, 0}}, {{0, 1, 1, 1, 0}, {1, 1, 0, 1, 1}}, {{0, 1, 1, 1, 1}, {1, 1, 0, 0, 1}}, {{ 1, 0, 0, 0, 1}, {1, 1, 1, 1, 1}}, {{0, 0, 0, 0, 0, 1}, {1, 1, 1, 1, 1, 1}}, {{0, 0, 0, 0, 1, 0}, {1, 1, 1, 1, 1, 1}}, {{0, 0, 0, 0, 1, 1}, {1, 1, 1, 1, 1, 0}}, {{0, 0, 0, 1, 0, 0}, {1, 1, 1, 1, 1, 1}}, {{0, 0, 0, 1, 1, 1}, {1, 1, 1, 1, 0, 0}}, {{0, 0, 1}, {1, 1, 1}, {1, 1, 1}}, {{0, 1, 0}, {1, 1, 1}, {1, 1, 1}}, {{0, 1, 1}, {1, 0, 1}, {1, 1, 1}}, {{0, 1, 1}, {1, 1, 0}, {1, 1, 1}}, {{0, 1, 1}, { 1, 1, 1}, {1, 1, 0}}, {{1, 0, 1}, {1, 0, 1}, {1, 1, 1}}, {{1, 0, 1}, {1, 1, 1}, {1, 0, 1}}, {{0, 0, 0, 1}, {0, 0, 1, 1}, {1, 1, 1, 1}}, {{0, 0, 0, 1}, {0, 1, 0, 1}, {1, 1, 1, 1}}, {{0, 0, 0, 1}, {0, 1, 1, 1}, {1, 1, 0, 1}}, {{0, 0, 0, 1}, {0, 1, 1, 1}, {1, 1, 1, 0}}, {{0, 0, 0, 1}, {1, 0, 0, 1}, {1, 1, 1, 1}}, {{0, 0, 0, 1}, {1, 0, 1, 1}, {1, 1, 1, 0}}, {{0, 0, 0, 1}, {1, 1, 0, 1}, {0, 1, 1, 1}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {0, 0, 1, 1}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {0, 1, 0, 1}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {0, 1, 1, 0}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {1, 0, 0, 1}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {1, 0, 1, 0}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {1, 1, 0, 0}}, {{0, 0, 1, 0}, {0, 0, 1, 1}, {1, 1, 1, 1}}, {{0, 0, 1, 0}, {0, 1, 1, 0}, {1, 1, 1, 1}}, {{0, 0, 1, 0}, {0, 1, 1, 1}, {1, 1, 0, 1}}, {{0, 0, 1, 0}, {0, 1, 1, 1}, {1, 1, 1, 0}}, {{0, 0, 1, 0}, {1, 0, 1, 0}, {1, 1, 1, 1}}, {{0, 0, 1, 0}, {1, 0, 1, 1}, {1, 1, 1, 0}}, {{0, 0, 1, 0}, {1, 1, 1, 0}, {0, 1, 1, 1}}, {{0, 0, 1, 0}, {1, 1, 1, 0}, {1, 0, 1, 1}}, {{0, 0, 1, 0}, {1, 1, 1, 1}, {0, 0, 1, 1}}, {{0, 0, 1, 0}, {1, 1, 1, 1}, {0, 1, 0, 1}}, {{0, 0, 1, 0}, {1, 1, 1, 1}, {0, 1, 1, 0}}, {{0, 0, 1, 0}, {1, 1, 1, 1}, {1, 0, 0, 1}}, {{0, 0, 1, 0}, {1, 1, 1, 1}, {1, 0, 1, 0}}, {{0, 0, 1, 0}, {1, 1, 1, 1}, {1, 1, 0, 0}}, {{0, 0, 1, 1}, {0, 0, 0, 1}, {1, 1, 1, 1}}, {{0, 0, 1, 1}, {0, 0, 1, 0}, {1, 1, 1, 1}}, {{0, 0, 1, 1}, {0, 0, 1, 1}, {1, 1, 1, 0}}, {{0, 0, 1, 1}, {0, 1, 1, 0}, {1, 1, 1, 0}}, {{0, 0, 1, 1}, {0, 1, 1, 1}, {1, 1, 0, 0}}, {{0, 0, 1, 1}, {1, 0, 1, 0}, {1, 1, 1, 0}}, {{0, 0, 1, 1}, {1, 1, 1, 0}, {0, 0, 1, 1}}, {{0, 0, 1, 1}, {1, 1, 1, 0}, {0, 1, 1, 0}}, {{0, 0, 1, 1}, {1, 1, 1, 0}, {1, 0, 1, 0}}, {{0, 1, 1, 0}, {0, 0, 1, 0}, {1, 1, 1, 1}}, {{0, 1, 1, 0}, {0, 0, 1, 1}, {1, 1, 1, 0}}, {{0, 1, 1, 1}, {0, 0, 1, 0}, {1, 1, 1, 0}}, {{0, 0, 0, 0, 1}, {0, 0, 0, 0, 1}, {1, 1, 1, 1, 1}}, {{0, 0, 0, 0, 1}, {0, 0, 0, 1, 1}, {1, 1, 1, 1, 0}}, {{ 0, 0, 0, 0, 1}, {0, 0, 1, 1, 1}, {1, 1, 1, 0, 0}}, {{0, 0, 0, 0, 1}, {0, 1, 1, 1, 1}, {1, 1, 0, 0, 0}}, {{0, 0, 0, 0, 1}, {1, 1, 1, 1, 1}, {0, 0, 0, 0, 1}}, {{0, 0, 0, 0, 1}, {1, 1, 1, 1, 1}, {0, 0, 0, 1, 0}}, {{0, 0, 0, 0, 1}, {1, 1, 1, 1, 1}, {0, 0, 1, 0, 0}}, {{ 0, 0, 0, 0, 1}, {1, 1, 1, 1, 1}, {0, 1, 0, 0, 0}}, {{0, 0, 0, 0, 1}, {1, 1, 1, 1, 1}, {1, 0, 0, 0, 0}}, {{0, 0, 0, 1, 0}, {0, 0, 0, 1, 0}, {1, 1, 1, 1, 1}}, {{0, 0, 0, 1, 0}, {0, 0, 0, 1, 1}, {1, 1, 1, 1, 0}}, {{0, 0, 0, 1, 0}, {0, 0, 1, 1, 1}, {1, 1, 1, 0, 0}}, {{ 0, 0, 0, 1, 0}, {0, 1, 1, 1, 1}, {1, 1, 0, 0, 0}}, {{0, 0, 0, 1, 0}, {1, 1, 1, 1, 0}, {0, 0, 0, 1, 1}}, {{0, 0, 0, 1, 0}, {1, 1, 1, 1, 1}, {0, 0, 0, 1, 0}}, {{0, 0, 0, 1, 0}, {1, 1, 1, 1, 1}, {0, 0, 1, 0, 0}}, {{0, 0, 0, 1, 0}, {1, 1, 1, 1, 1}, {0, 1, 0, 0, 0}}, {{ 0, 0, 0, 1, 1}, {0, 0, 0, 1, 0}, {1, 1, 1, 1, 0}}, {{0, 0, 0, 1, 1}, {0, 0, 1, 1, 0}, {1, 1, 1, 0, 0}}, {{0, 0, 0, 1, 1}, {0, 1, 1, 1, 0}, {1, 1, 0, 0, 0}}, {{0, 0, 0, 1, 1}, {1, 1, 1, 1, 0}, {0, 0, 1, 0, 0}}, {{0, 0, 1, 0, 0}, {0, 0, 1, 0, 0}, {1, 1, 1, 1, 1}}, {{ 0, 0, 1, 0, 0}, {0, 0, 1, 1, 1}, {1, 1, 1, 0, 0}}, {{0, 0, 1, 0, 0}, {1, 1, 1, 1, 1}, {0, 0, 1, 0, 0}}, {{0, 0, 1, 1, 1}, {0, 0, 1, 0, 0}, {1, 1, 1, 0, 0}}, {{0, 0, 0, 1}, {0, 0, 0, 1}, {0, 0, 0, 1}, {1, 1, 1, 1}}, {{0, 0, 0, 1}, {0, 0, 0, 1}, {0, 0, 1, 1}, {1, 1, 1, 0}}, {{0, 0, 0, 1}, {0, 0, 0, 1}, {0, 1, 1, 1}, {1, 1, 0, 0}}, {{0, 0, 0, 1}, {0, 0, 0, 1}, {1, 1, 1, 1}, {0, 0, 0, 1}}, {{0, 0, 0, 1}, {0, 0, 0, 1}, {1, 1, 1, 1}, {0, 0, 1, 0}}, {{0, 0, 0, 1}, {0, 0, 0, 1}, {1, 1, 1, 1}, {0, 1, 0, 0}}, {{0, 0, 0, 1}, {0, 0, 0, 1}, {1, 1, 1, 1}, {1, 0, 0, 0}}, {{0, 0, 0, 1}, {0, 0, 1, 1}, {0, 1, 1, 0}, {1, 1, 0, 0}}, {{0, 0, 0, 1}, {0, 0, 1, 1}, {1, 1, 1, 0}, {0, 0, 1, 0}}, {{0, 0, 0, 1}, {0, 0, 1, 1}, {1, 1, 1, 0}, {0, 1, 0, 0}}, {{0, 0, 0, 1}, {0, 0, 1, 1}, {1, 1, 1, 0}, {1, 0, 0, 0}}, {{0, 0, 0, 1}, {0, 1, 1, 1}, {0, 1, 0, 0}, {1, 1, 0, 0}}, {{0, 0, 0, 1}, {0, 1, 1, 1}, {1, 1, 0, 0}, {0, 1, 0, 0}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {0, 0, 1, 0}, {0, 0, 1, 0}}, {{0, 0, 0, 1}, {1, 1, 1, 1}, {0, 1, 0, 0}, {0, 1, 0, 0}}, {{0, 0, 1, 0}, {0, 0, 1, 0}, {1, 1, 1, 1}, {0, 0, 1, 0}}, {{0, 0, 1, 0}, {0, 0, 1, 0}, {1, 1, 1, 1}, {0, 1, 0, 0}}, {{0, 0, 1, 0}, {0, 0, 1, 1}, {1, 1, 1, 0}, {0, 1, 0, 0}}}; ResourceFunction["CanonicalTilingMask"][RandomChoice[heptominoes]]
Out[9]=

For masks using five bits and having a maximum dimension of 4, there are 192 canonical cases, shown below:

In[10]:=
allMasks44bit5 = ResourceFunction["ArrayPatternFromIndex"][#] & /@ {{{2, 4}, 31, 2}, {{ 2, 4}, 59, 2}, {{2, 4}, 91, 2}, {{2, 4}, 121, 2}, {{2, 4}, 155, 2}, {{3, 4}, 283, 2}, {{3, 4}, 285, 2}, {{3, 4}, 299, 2}, {{3, 4}, 301, 2}, {{3, 4}, 313, 2}, {{3, 4}, 331, 2}, {{3, 4}, 333, 2}, {{ 3, 4}, 345, 2}, {{3, 4}, 361, 2}, {{3, 4}, 391, 2}, {{3, 4}, 395, 2}, {{3, 4}, 397, 2}, {{3, 4}, 398, 2}, {{3, 4}, 403, 2}, {{3, 4}, 405, 2}, {{3, 4}, 406, 2}, {{3, 4}, 410, 2}, {{3, 4}, 412, 2}, {{ 3, 4}, 419, 2}, {{3, 4}, 422, 2}, {{3, 4}, 425, 2}, {{3, 4}, 426, 2}, {{3, 4}, 433, 2}, {{3, 4}, 434, 2}, {{3, 4}, 436, 2}, {{3, 4}, 440, 2}, {{3, 4}, 451, 2}, {{3, 4}, 453, 2}, {{3, 4}, 454, 2}, {{ 3, 4}, 457, 2}, {{3, 4}, 458, 2}, {{3, 4}, 465, 2}, {{3, 4}, 466, 2}, {{3, 4}, 468, 2}, {{3, 4}, 481, 2}, {{3, 4}, 482, 2}, {{3, 4}, 651, 2}, {{3, 4}, 653, 2}, {{3, 4}, 665, 2}, {{3, 4}, 666, 2}, {{ 3, 4}, 681, 2}, {{3, 4}, 713, 2}, {{3, 4}, 793, 2}, {{3, 4}, 809, 2}, {{3, 4}, 899, 2}, {{3, 4}, 901, 2}, {{3, 4}, 902, 2}, {{3, 4}, 905, 2}, {{3, 4}, 906, 2}, {{3, 4}, 1305, 2}, {{3, 4}, 1306, 2}, {{3, 4}, 1321, 2}, {{3, 4}, 1322, 2}, {{3, 4}, 1353, 2}, {{3, 4}, 1417, 2}, {{3, 4}, 1561, 2}, {{3, 4}, 1577, 2}, {{3, 4}, 2345, 2}, {{4, 4}, 4123, 2}, {{4, 4}, 4125, 2}, {{4, 4}, 4139, 2}, {{4, 4}, 4185, 2}, {{4, 4}, 4231, 2}, {{4, 4}, 4235, 2}, {{4, 4}, 4237, 2}, {{4, 4}, 4238, 2}, {{4, 4}, 4243, 2}, {{4, 4}, 4245, 2}, {{4, 4}, 4246, 2}, {{4, 4}, 4250, 2}, {{4, 4}, 4252, 2}, {{4, 4}, 4259, 2}, {{4, 4}, 4261, 2}, {{4, 4}, 4262, 2}, {{4, 4}, 4265, 2}, {{4, 4}, 4266, 2}, {{4, 4}, 4273, 2}, {{4, 4}, 4274, 2}, {{4, 4}, 4276, 2}, {{4, 4}, 4280, 2}, {{4, 4}, 4291, 2}, {{4, 4}, 4293, 2}, {{4, 4}, 4294, 2}, {{4, 4}, 4297, 2}, {{4, 4}, 4305, 2}, {{4, 4}, 4306, 2}, {{4, 4}, 4308, 2}, {{4, 4}, 4312, 2}, {{4, 4}, 4321, 2}, {{4, 4}, 4322, 2}, {{4, 4}, 4483, 2}, {{4, 4}, 4485, 2}, {{4, 4}, 4486, 2}, {{4, 4}, 4490, 2}, {{4, 4}, 4500, 2}, {{4, 4}, 4513, 2}, {{4, 4}, 4545, 2}, {{4, 4}, 4546, 2}, {{4, 4}, 4739, 2}, {{4, 4}, 4741, 2}, {{4, 4}, 4745, 2}, {{4, 4}, 4753, 2}, {{4, 4}, 4756, 2}, {{4, 4}, 4769, 2}, {{4, 4}, 4801, 2}, {{4, 4}, 4993, 2}, {{4, 4}, 5131, 2}, {{4, 4}, 5133, 2}, {{4, 4}, 5146, 2}, {{4, 4}, 5148, 2}, {{4, 4}, 5193, 2}, {{4, 4}, 5251, 2}, {{4, 4}, 5253, 2}, {{4, 4}, 5257, 2}, {{4, 4}, 5265, 2}, {{4, 4}, 5281, 2}, {{4, 4}, 5313, 2}, {{4, 4}, 5505, 2}, {{4, 4}, 5761, 2}, {{4, 4}, 6151, 2}, {{4, 4}, 6155, 2}, {{4, 4}, 6157, 2}, {{4, 4}, 6158, 2}, {{4, 4}, 6163, 2}, {{4, 4}, 6165, 2}, {{4, 4}, 6166, 2}, {{4, 4}, 6172, 2}, {{4, 4}, 6179, 2}, {{4, 4}, 6181, 2}, {{4, 4}, 6182, 2}, {{4, 4}, 6185, 2}, {{4, 4}, 6186, 2}, {{4, 4}, 6194, 2}, {{4, 4}, 6196, 2}, {{4, 4}, 6200, 2}, {{4, 4}, 6211, 2}, {{4, 4}, 6213, 2}, {{4, 4}, 6214, 2}, {{4, 4}, 6217, 2}, {{4, 4}, 6228, 2}, {{4, 4}, 6242, 2}, {{4, 4}, 6275, 2}, {{4, 4}, 6277, 2}, {{4, 4}, 6278, 2}, {{4, 4}, 6290, 2}, {{4, 4}, 6292, 2}, {{4, 4}, 6305, 2}, {{4, 4}, 6306, 2}, {{4, 4}, 6337, 2}, {{4, 4}, 6403, 2}, {{4, 4}, 6405, 2}, {{4, 4}, 6406, 2}, {{4, 4}, 6410, 2}, {{4, 4}, 6418, 2}, {{4, 4}, 6420, 2}, {{4, 4}, 6434, 2}, {{4, 4}, 6466, 2}, {{4, 4}, 6530, 2}, {{4, 4}, 6659, 2}, {{4, 4}, 6661, 2}, {{4, 4}, 6662, 2}, {{4, 4}, 6665, 2}, {{4, 4}, 6676, 2}, {{4, 4}, 6690, 2}, {{4, 4}, 6914, 2}, {{4, 4}, 7171, 2}, {{4, 4}, 7173, 2}, {{4, 4}, 7177, 2}, {{4, 4}, 7186, 2}, {{4, 4}, 7188, 2}, {{4, 4}, 7202, 2}, {{4, 4}, 7426, 2}, {{4, 4}, 8339, 2}, {{4, 4}, 8341, 2}, {{4, 4}, 8345, 2}, {{4, 4}, 8585, 2}, {{4, 4}, 10261, 2}, {{4, 4}, 10262, 2}, {{4, 4}, 10265, 2}, {{4, 4}, 10266, 2}, {{4, 4}, 10292, 2}, {{4, 4}, 10386, 2}, {{4, 4}, 10505, 2}, {{ 4, 4}, 10506, 2}, {{4, 4}, 12425, 2}, {{4, 4}, 14345, 2}, {{4, 4}, 22537, 2}}; Grid[ Partition[ ArrayPlot[3 # + 1, PixelConstrained -> 6, Frame -> False] & /@ allMasks44bit5, 24], Frame -> All]
Out[10]=

An exercise to test them all is left as an exercise for the reader. Meanwhile, here we test three of these at random:

In[11]:=
ran = RandomSample[allMasks44bit5, 3]; (ResourceFunction["CanonicalTilingMask"] /@ ran) == ran
Out[12]=

Version History

  • 1.0.0 – 29 July 2022

Related Resources

License Information