Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 CanonicalKnuthBendixCompletion

Source Notebook

Compute the canonical Knuth-Bendix completion for a given multiway system

Contributed by: Jonathan Gorard

ResourceFunction["CanonicalKnuthBendixCompletion"][rules]

generates a list of canonical (i.e. initial condition-independent) Knuth-Bendix completion rules for the multiway system with the specified rules.

ResourceFunction["CanonicalKnuthBendixCompletion"][rules,n]

generates a list of canonical (i.e. initial condition-independent) Knuth-Bendix completion rules for the multiway system with the specified rules after n steps.

Details and Options

Rules can be specified in the following ways:
{"lhs1"->"rhs1",…}string substitution system
{{l11,l12,…}->{r11,r12,..},…}list substitution system
WolframModel[rules]Wolfram Model system
CellularAutomaton[rules]cellular automaton system
"type"→rulessystem of the specified type
Supported rule types include:
"StringSubstitutionSystem"rules given as replacements on strings
"ListSubstitutionSystem"rules given as replacements on lists
"CellularAutomaton"rules given as a list of CellularAutomaton rule specifications
"WolframModel"rules given as replacements on hypergraphs
ResourceFunction["CanonicalKnuthBendixCompletion"] accepts both indiviudal rules and lists of rules.
Knuth-Bendix completion transforms an arbitrary rewrite system into a confluent (causal invariant) rewrite system by resolving critical pairs.
In the context of the multiway systems, critical (branch) pairs indicate bifurcations or ambiguities in the multiway evolution.
ResourceFunction["CanonicalKnuthBendixCompletion"] gives the minimal set of rules required to force all unresolved canonical branch pairs to converge.

Examples

Basic Examples (2) 

Generate the list of all canonical Knuth-Bendix completion rules for a string substitution system:

In[1]:=
ResourceFunction[ "CanonicalKnuthBendixCompletion"][{"AA" -> "ABA", "AAA" -> "B"}]
Out[1]=

Generate the list of canonical Knuth-Bendix completion rules necessary to force confluence after 2 steps:

In[2]:=
ResourceFunction[ "CanonicalKnuthBendixCompletion"][{"AA" -> "ABA", "AAA" -> "B"}, 2]
Out[2]=

CanonicalKnuthBendixCompletion can handle Wolfram models and other system types:

In[3]:=
ResourceFunction["CanonicalKnuthBendixCompletion"][ "WolframModel" -> {{{2, 2, 1}, {2, 2, 2}} -> {{1, 1, 3}, {3, 3, 2}}}]
Out[4]=
In[5]:=
Take[ResourceFunction["CanonicalKnuthBendixCompletion"][ "WolframModel" -> {{{2, 2, 1}, {2, 2, 2}} -> {{1, 1, 3}, {3, 3, 2}}}, 10], 20]
Out[5]=

Provide a cellular automaton as input:

In[6]:=
Take[ResourceFunction["CanonicalKnuthBendixCompletion"][ CellularAutomaton[30], 2], 20]
Out[6]=

Scope (4) 

System Types (4) 

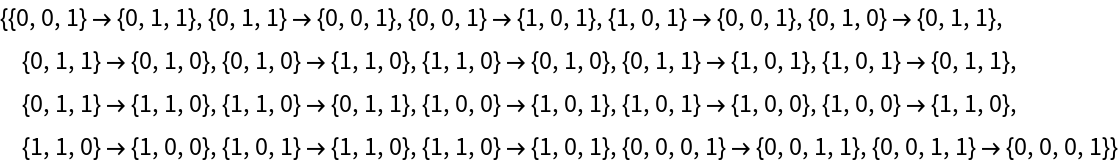
CanonicalKnuthBendixCompletion supports both string and list substitution systems:

In[7]:=
ResourceFunction[ "CanonicalKnuthBendixCompletion"][{"BB" -> "AA", "ABB" -> "BA"}]
Out[7]=

Use substitutions on lists:

In[8]:=
ResourceFunction[ "CanonicalKnuthBendixCompletion"][{{1, 1} -> {0, 0}, {0, 1, 1} -> {1, 0}}]
Out[8]=

CanonicalKnuthBendixCompletion also supports multiway generalizations of cellular automata:

In[9]:=
Take[ResourceFunction["CanonicalKnuthBendixCompletion"][ CellularAutomaton[{170, 240}]], 20]
Out[9]=

Generate a Knuth-Bendix completion for left- and right-shift cellular automaton rules after 5 steps:

In[10]:=
Take[ResourceFunction["CanonicalKnuthBendixCompletion"][ CellularAutomaton[{170, 240}], 5], 20]
Out[10]=

Determine that the rule 30 cellular automaton is not total causal invariant:

In[11]:=
Take[ResourceFunction["CanonicalKnuthBendixCompletion"][ CellularAutomaton[30], 5], 20]
Out[11]=

CanonicalKnuthBendixCompletion also supports multiway generalizations of Wolfram Models:

In[12]:=
ResourceFunction["CanonicalKnuthBendixCompletion"][ "WolframModel" -> {{{2, 2, 1}, {2, 2, 2}} -> {{1, 1, 2}, {2, 2, 2}}}]
Out[12]=

Determine that this Wolfram model rule is not total causal invariant:

In[13]:=
Take[ResourceFunction["CanonicalKnuthBendixCompletion"][ "WolframModel" -> {{{2, 2, 1}, {2, 2, 2}} -> {{1, 1, 2}, {2, 2, 2}}}, 5], 20]
Out[13]=

Applications (2) 

Causal Invariant Rules (2) 

Prove that the Xor and And functions are total causal invariant (due to associativity):

In[14]:=
ResourceFunction[ "CanonicalKnuthBendixCompletion"][{"TT" -> "F", "TF" -> "T", "FT" -> "T", "FF" -> "F"}, 1]
Out[14]=
In[15]:=
ResourceFunction[ "CanonicalKnuthBendixCompletion"][{"TT" -> "T", "TF" -> "F", "FT" -> "F", "FF" -> "F"}, 1]
Out[15]=

On the other hand, the Nand function is not associative, so it is not total causal invariant:

In[16]:=
ResourceFunction[ "CanonicalKnuthBendixCompletion"][{"TT" -> "F", "TF" -> "T", "FT" -> "T", "FF" -> "T"}, 1]
Out[16]=

Properties and Relations (1) 

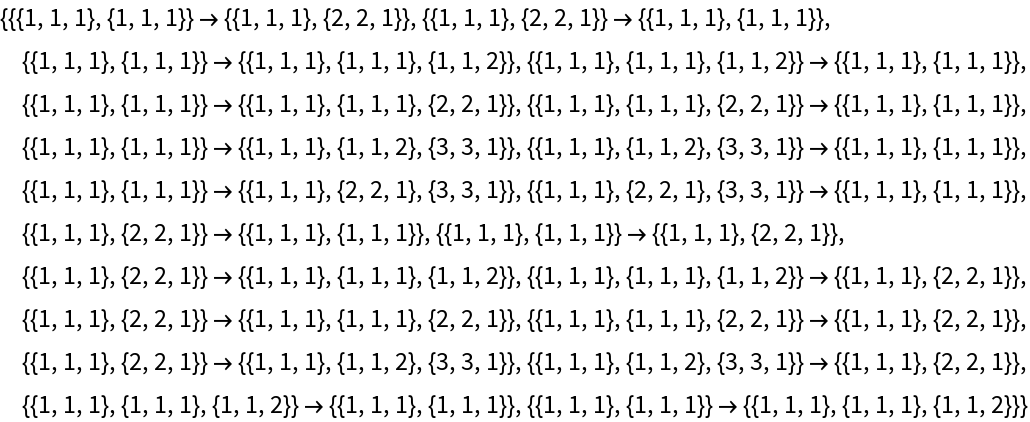
CanonicalKnuthBendixCompletion returns an empty list of canonical Knuth-Bendix completion rules if and only if the rule is total causal invariant:

In[17]:=
ResourceFunction[ "CanonicalKnuthBendixCompletion"][{"TT" -> "F", "TF" -> "T", "FT" -> "T", "FF" -> "T"}, 1]
Out[17]=
In[18]:=
ResourceFunction[ "CanonicalKnuthBendixCompletion"][{"TT" -> "F", "TF" -> "T", "FT" -> "T", "FF" -> "F"}, 1]
Out[18]=

Version History

  • 1.0.0 – 13 April 2020

Source Metadata

  • Citation:
    • Stephen Wolfram (2002), “A New Kind of Science”
    • Stephen Wolfram (2020), “A Class of Models with Potential to Represent Fundamental Physics”
    • Jonathan Gorard (2020), “Some Relativistic and Gravitational Properties of the Wolfram Model”
    • Jonathan Gorard (2020), “Some Quantum Mechanical Properties of the Wolfram Model”

Related Resources

License Information