Function Repository Resource:

CATransducerGraph

Obtain an annotated state transition graph for any CellularAutomaton rule

Contributed by: Brad Klee

ResourceFunction["CATransducerGraph"][rule,k,r]

returns a directed adjacency graph over k^{(k^2r+1)} states, where each edge is annotated with an input value 0, 1, …, k and each vertex is annotated with an output value determined by rule.

Details

The process of updating one row of a CellularAutomaton to the next requires the specification of a rule and a procedure for scanning through blocks of the input row. Once the transition function is named, this process is well described by a Moore Machine, which is a type of Finite State Transducer (FST).

ResourceFunction["CATransducerGraph"] accepts an option "Shift" whose default value Right can be changed to Left. Respectively, these option values determine if the FST transition function should read blocks of the input tape sequentially from Left to Right or vice versa. For asymmetric rules such as the Elementary Cellular Automaton (ECA) 30, a putatively better result can be obtained when reading from Right to Left by setting "Shift” → Left.

Each shift from one state to the next drops a value from either the left or right side and adds a new value on the opposite side. Added values are annotated on edges while removed values are annotated on vertices. These values can be accessed and extracted using AnnotationValue.

ResourceFunction["CATransducerGraph"] accepts an option "VertexFigures" which automates stylish embellishment. If set to Automatic, the vertices are colored by their annotation values. If set to True, vertices depict the input-output rule as in RulePlot.

ResourceFunction["CATransducerGraph"] accepts either ColorRules or ColorFunction for finer control of automated vertex styling.

ResourceFunction["CATransducerGraph"] also accepts any of the typical Graph options.

The expression k^{(k^2r+1)} grows extremely rapidly with k. Be aware that higher k values may lead to unacceptably long calculation time.

Examples

Basic Examples (3)

The CATransducerGraph for Rule 86:

In[1]:=

Out[1]=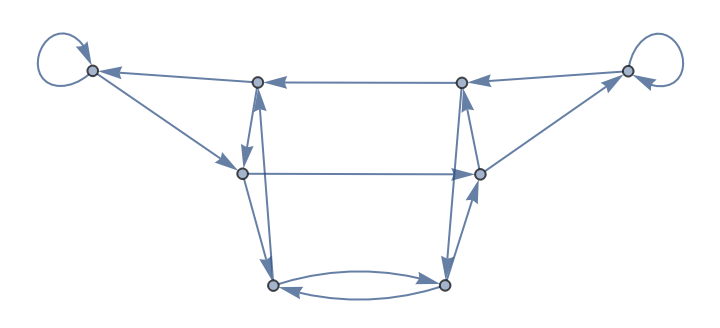

Obtain the definition of rule 86 from Annotation data:

In[2]:=

Out[2]=

Prove that rule 86 allows any bit vector in its range of outputs:

In[3]:=

Out[3]=

Map a two-state CA with CATransducerGraph over different radius values:

In[4]:=

Out[4]=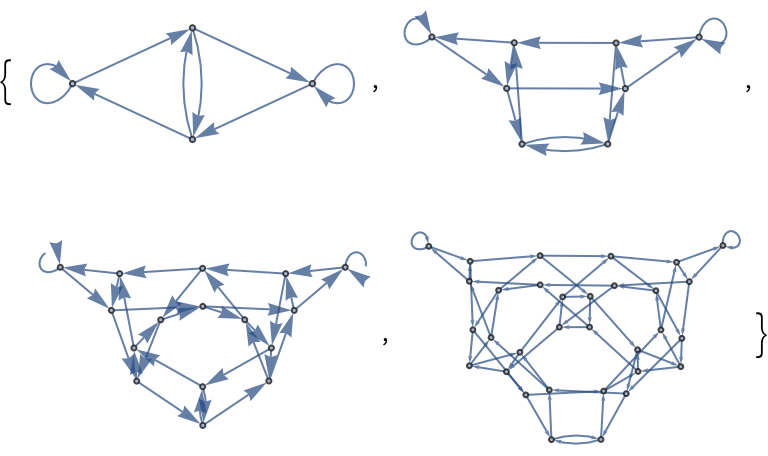

Color a CATransducerGraph according to its Annotation data:

In[5]:=

With[{graph = ResourceFunction["CATransducerGraph"][90, 2, 1]},
Graph[graph, VertexSize -> Large, VertexStyle -> Map[
# -> Association[0 -> Darker[Green, .1], 1 -> Darker[Yellow, .1]][
AnnotationValue[{graph, #}, VertexWeight]] &, VertexList[graph]],
EdgeStyle -> Map[# -> Association[0 -> Red, 1 -> Blue][
AnnotationValue[{graph, #}, EdgeWeight]] &, EdgeList[graph]]]
]

Out[5]=

Scope (2)

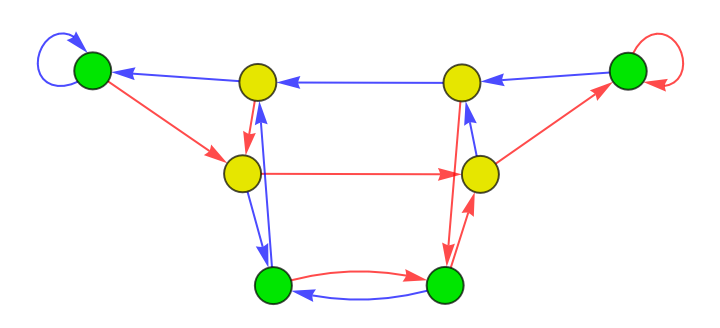Map a three-state with CATransducerGraph over different radius values:

In[6]:=

Out[6]=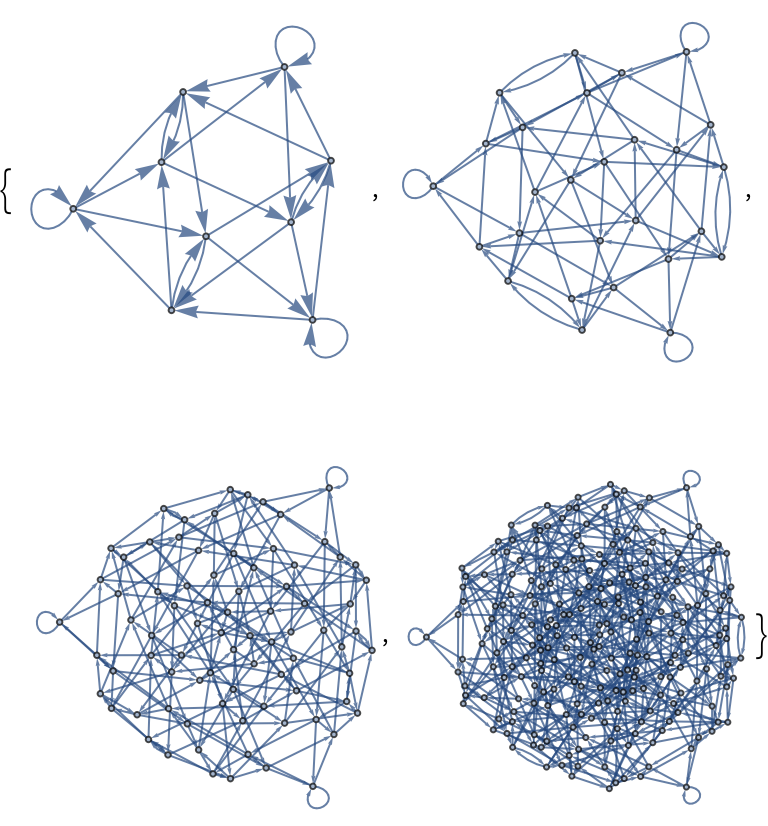

Obtain the CATransducerGraph for a totalistic rule:

In[7]:=

Out[7]=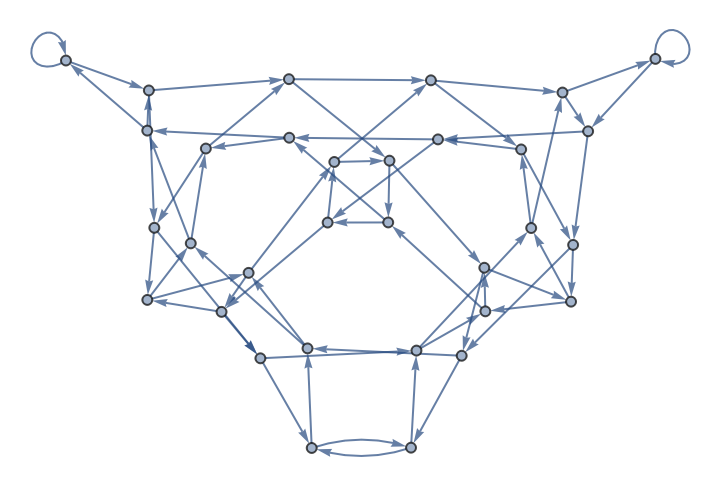

Options (4)

Color vertices according to the transduced output value:

In[8]:=

$ResourceFunction["CATransducerGraph"][{10, {2, 1}, 2}, 2, 2, "VertexFigures" -> Automatic, VertexSize -> Large, ColorRules -> {1 -> Darker[Orange, .2], 0 -> Lighter[Blend[{Yellow, Orange}]], _ -> LightGray} ]$

Out[8]=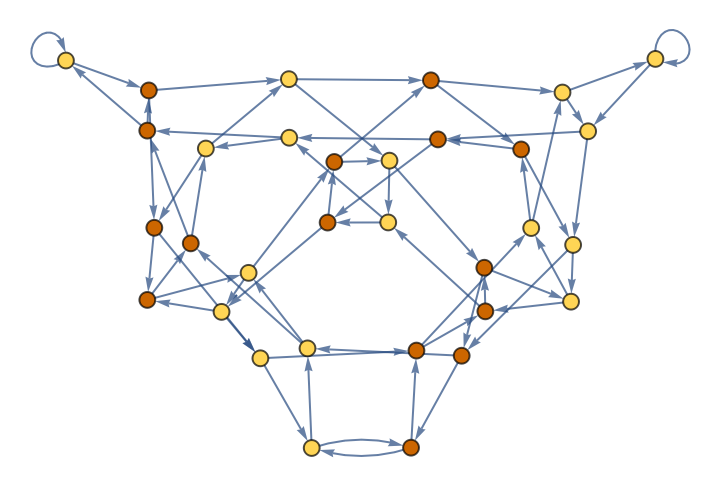

Show fragments of input and output tapes:

In[9]:=

$ResourceFunction["CATransducerGraph"][{10, {2, 1}, 2}, 2, 2, "VertexFigures" -> True, VertexSize -> 1/2, EdgeStyle -> Gray, ColorRules -> {1 -> Darker[Orange, .2], 0 -> Lighter[Blend[{Yellow, Orange}]], _ -> LightGray} ]$

Out[9]=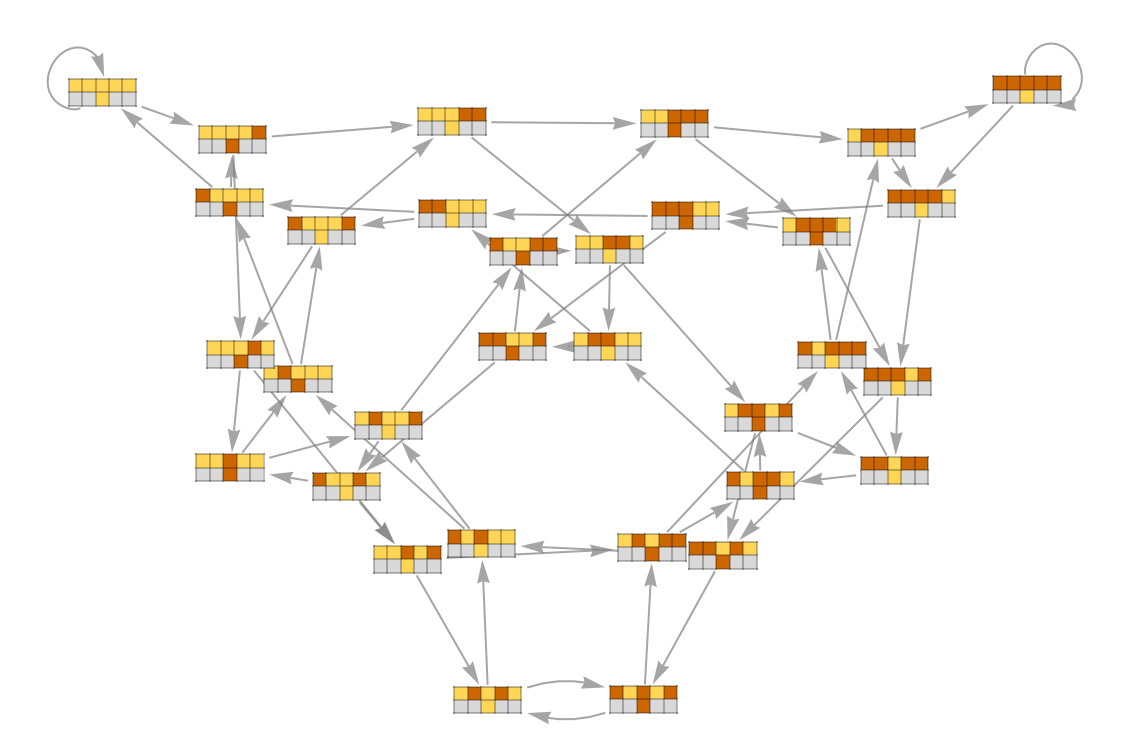

Compare left-shift and right-shift graphs for rule 30:

In[10]:=

Out[10]=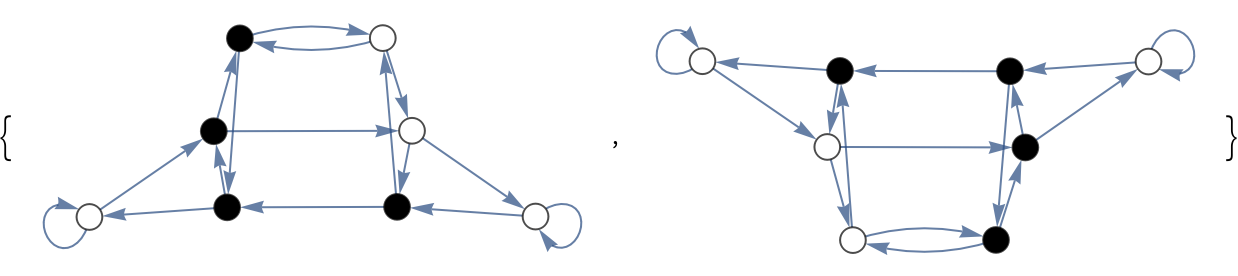

One graph has uniform outputs, the other does not:

In[11]:=

Function[graph, Values[Union[
AnnotationValue[{graph, #}, VertexWeight]] & /@ KeySort[
GroupBy[EdgeList[graph], First -> Last]]]] /@ gs

Out[11]=

Highlight where the right-shift graph fails to provide alternatives for the next transduced value:

In[12]:=

With[{badEs = Catenate[Values[
Select[GroupBy[EdgeList[Last[gs]], First -> Identity], Apply[SameQ,
AnnotationValue[{Last[gs], Last[#]}, VertexWeight] & /@ #] &]]]},
HighlightGraph[Last[gs], badEs]
]

Out[12]=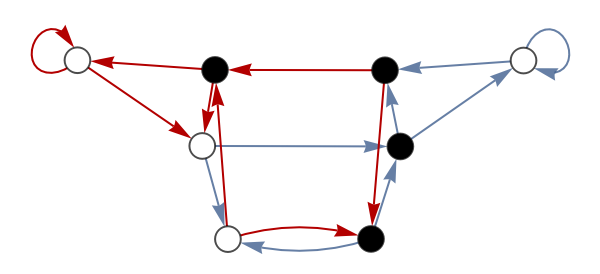

Add vertex figures to the CATransducerGraph of a random four-color CellularAutomaton:

In[13]:=

ResourceFunction["CATransducerGraph"][SeedRandom[123]; RandomInteger[4^4^3 - 1], 4, 1, VertexSize -> 2/3,
EdgeStyle -> Gray, "VertexFigures" -> True]

Out[13]=

Applications (2)

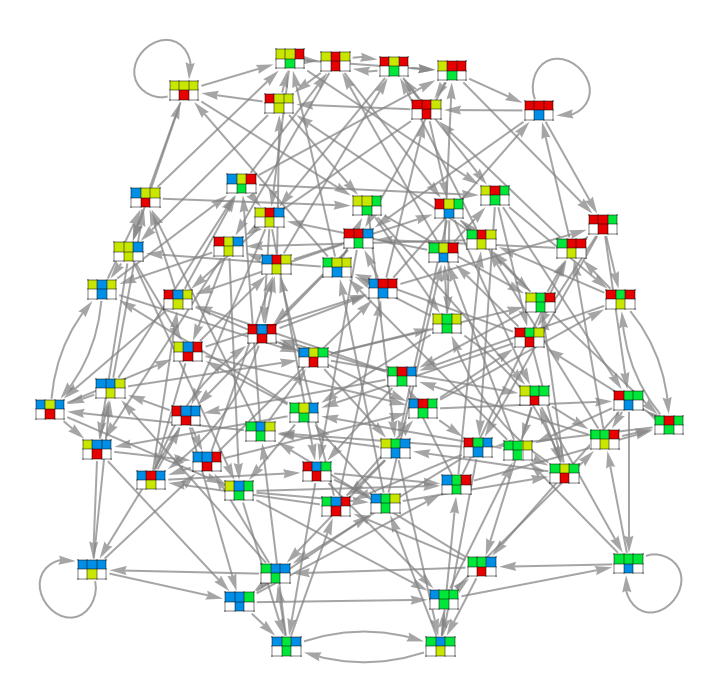Prove that a certain length-36 bit vector can not exist in a totalistic CA using rule 10:

In[14]:=

Module[
{graph, seq, alts, level, res},
graph = ResourceFunction["CATransducerGraph"][{10, {2, 1}, 2}, 2, 2];
seq = {1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0,
1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1};
alts = GroupBy[Transpose[{VertexList[graph],
AnnotationValue[graph, VertexWeight]}],
Last -> First];
level = alts[First[seq]];
res = Fold[Function[{lev, val},
Union[Select[alts[val],
MemberQ[Rest /@ lev, Most[#]] &]]
], level, Rest[seq]];
Labeled[ArrayPlot[{seq}, Mesh -> True],
"Non-invertible?" -> SameQ[res, {}]]
]

Out[14]=

Given a random bit vector, list possible pre-images under rule 165:

In[15]:=

$Module[{graph, edges, rule, path, res}, graph = ResourceFunction["CATransducerGraph"][165, 2, 1]; edges = GroupBy[EdgeList[graph], First -> Last]; rule = Association[Thread[Rule[VertexList[graph], AnnotationValue[graph, VertexWeight]]]]; SeedRandom[323]; path = RandomInteger[1, 10]; res = Map[FoldList[ Function[{state, val}, SelectFirst[edges[state], SameQ[rule[#], val] &] ], #, Rest[path]] &, Select[VertexList[graph], SameQ[rule[#] , First[path]] &] ]; ArrayPlot[ {Join[Most[First[#]], Last /@ Rest[#]], CenterArray[path, Length[path] + 2, _]}, Mesh -> True, ColorRules -> {1 -> Black, 0 -> White, _ -> LightRed} ] & /@ res ]$

Out[15]=

Properties and Relations (2)

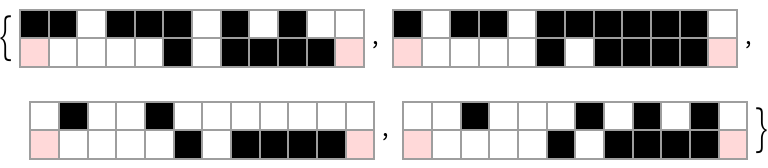The structure of CATransducerGraph does not depend on choice of rule:

In[16]:=

Out[16]=

However, different rules have different Annotation values:

In[17]:=

Out[17]=

Neat Examples (2)

Obtain a list of "multiway-invertible" elementary cellular automata:

In[18]:=

$cas = Union[ Catenate[Function[shift, Select[Range[0, 2^8 - 1], Function[graph, AllTrue[Values[GroupBy[EdgeList[graph], First -> Last]], SameQ[{0, 1}, Union[AnnotationValue[{graph, #}, VertexWeight] & /@ #]] &]][ ResourceFunction["CATransducerGraph"][#, 2, 1, "Shift" -> shift] ] &]] /@ {Left, Right}]]$