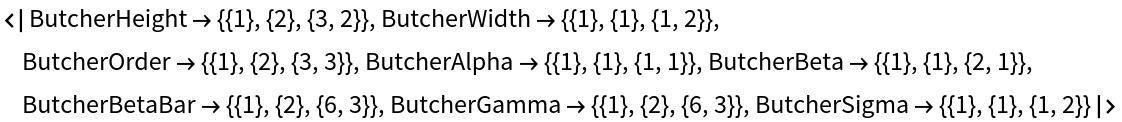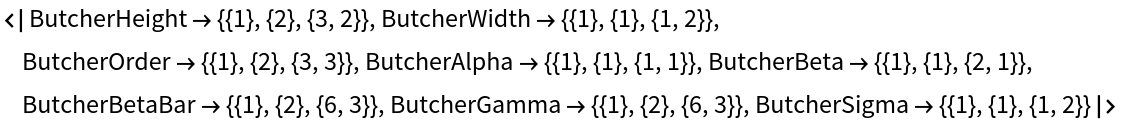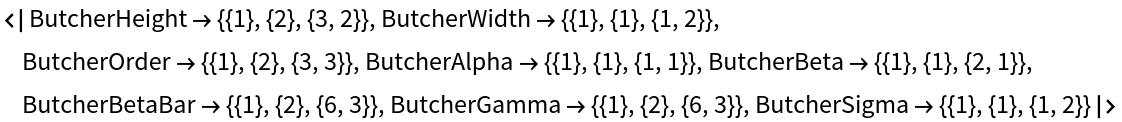Details and Options
For multiple trees, ResourceFunction["ButcherTreeData"][{tree1,tree2,…}] returns an association of the form <|"prop1"→{v11,v12,…},"prop2"→{v21,v22,…},…|>, where vij is the value of the property i of the tree j.
Possible characterics of tree include:
| "ButcherHeight" | the height of the tree |
| "ButcherWidth" | the width of the tree |
| "ButcherOrder" | the number of vertices in the tree |
| "ButcherGamma" | the density of the tree |
| "ButcherSigma" | the order of the symmetry group of the tree |
Characterics related to the number of possible ways of labeling tree are:
| "ButcherAlpha" | labeling with a totally ordered set of labels |
| "ButcherBeta" | labeling with all vertices labeled except for the root vertex |
| "ButcherBetaBar" | labeling with an unordered set of labels |
ResourceFunction["ButcherTreeData"][tree,"ButcherAlpha"] gives the number of ways of labeling the vertices of tree with a totally ordered set of labels such that if (m,n) is an edge, then m<n.
ResourceFunction["ButcherTreeData"][tree,"ButcherBeta"] gives the number of ways of labeling tree with Butcher order -1 distinct labels such that the root is not labeled, but every other vertex is labeled.
ResourceFunction["ButcherTreeData"][tree,{"ButcherBeta",n}] gives the number of ways of labeling n of the vertices of tree with n distinct labels such that every leaf is labeled and the root is not labeled.
ResourceFunction["ButcherTreeData"][tree,"ButcherBetaBar"] gives the number of ways of labeling tree with Butcher order distinct labels such that every vertex is labeled.
ResourceFunction["ButcherTreeData"][tree,{"ButcherBetaBar",n}] gives the number of ways of labeling n of the vertices of tree with n distinct labels such that every leaf is labeled.
The density returned by ResourceFunction["ButcherTreeData"][tree,"ButcherGamma"] is also the reciprocal of the right-hand side of the order condition imposed by tree.
ResourceFunction["ButcherTreeData"][tree] is equivalent to
ResourceFunction["ButcherTreeData"][tree,All] giving an association of the chracteristics of the tree.