Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate Bulirsch's incomplete elliptic integral of the third kind
ResourceFunction["BulirschEL3"][x,m,p] gives Bulirsch's incomplete elliptic integral of the third kind |
Evaluate numerically:
| In[1]:= |
|
| Out[1]= |
|
| In[2]:= |
|
| Out[2]= |
|
Evaluate numerically for complex arguments:
| In[3]:= |
|
| Out[3]= |
|
Evaluate to high precision:
| In[4]:= |
|
| Out[4]= |
|
The precision of the output tracks the precision of the input:
| In[5]:= |
|
| Out[5]= |
|
Simple exact results are generated automatically:
| In[6]:= |
|
| Out[6]= |
|
| In[7]:= |
|
| Out[7]= |
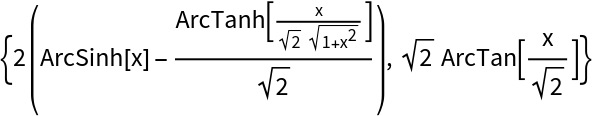
|
BulirschEL3 threads elementwise over lists:
| In[8]:= |
|
| Out[8]= |
|
Series expansion of BulirschEL3 at the origin:
| In[9]:= |
|
| Out[9]= |
|
Total arc length of a cornoid:
| In[10]:= |
|
| Out[10]= |
|
Compare with the result of ArcLength:
| In[11]:= |
|
| Out[11]= |
|
Visualize the solid angle subtended by a cylinder:
| In[12]:= |
|
| Out[12]= |
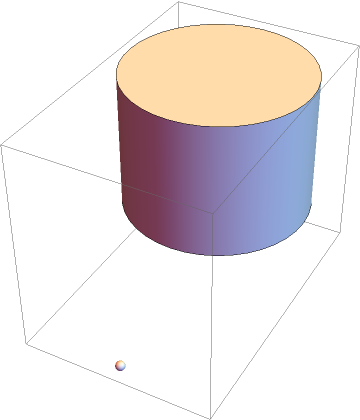
|
Evaluate the solid angle:
| In[13]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/52510be7-5435-42db-946a-21e2e5b98b36"]](https://www.wolframcloud.com/obj/resourcesystem/images/4b1/4b1117b7-e59e-46bc-a020-bb34cd4b0442/2399f7dc7cfa93ac.png)
|
| Out[13]= |
|
Compare with the result of NIntegrate:
| In[14]:= |
![With[{pc = {0, 2, 3/4}, r = 1, h = 3/2, prec = 20},
With[{b = r^2/Norm[Most[pc]], c = r Sqrt[1 - r^2/Norm[Most[pc]]^2], d = Norm[Most[pc]], zc = Last[pc]},
NIntegrate[(
2 (h + zc) Sqrt[r^2 - x1^2])/(((d + x1)^2 + (h + zc)^2) Sqrt[
d^2 + r^2 + 2 d x1 + (h + zc)^2]), {x1, -r, -b}, WorkingPrecision -> prec] + NIntegrate[(
2 zc Sqrt[r^2 - x1^2])/(((d + x1)^2 + zc^2) Sqrt[
d^2 + r^2 + 2 d x1 + zc^2]), {x1, -b, r}, WorkingPrecision -> prec] + NIntegrate[(
2 c (d - b))/(((d - b)^2 + (z1 + zc)^2) Sqrt[
c^2 + (d - b)^2 + (z1 + zc)^2]), {z1, 0, h}, WorkingPrecision -> prec]]]](https://www.wolframcloud.com/obj/resourcesystem/images/4b1/4b1117b7-e59e-46bc-a020-bb34cd4b0442/4fdc20aa1c115864.png)
|
| Out[14]= |
|
Both incomplete and complete cases of EllipticPi can be expressed in terms of BulirschEL3:
| In[15]:= |
|
| Out[15]= |
|
| In[16]:= |
|
| Out[16]= |
|
Express EllipticF and EllipticE in terms of BulirschEL3:
| In[17]:= |
|
| Out[17]= |
|
| In[18]:= |
![With[{\[Phi] = \[Pi]/5, m = 2/3}, N[{EllipticE[\[Phi], m], (1 - m) ResourceFunction["BulirschEL3"][Tan[\[Phi]], 1 - m, 1 - m] + (m Sin[2 \[Phi]])/(2 Sqrt[1 - m Sin[\[Phi]]^2])}]]](https://www.wolframcloud.com/obj/resourcesystem/images/4b1/4b1117b7-e59e-46bc-a020-bb34cd4b0442/76ae845ad135121f.png)
|
| Out[18]= |
|
Wolfram Language 12.3 (May 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License