Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate Bulirsch's incomplete elliptic integral of the second kind
ResourceFunction["BulirschEL2"][x,m,a,b] gives Bulirsch's incomplete elliptic integral of the second kind |
Evaluate numerically:
| In[1]:= |
|
| Out[1]= |
|
| In[2]:= |
|
| Out[2]= |
|
Evaluate numerically for complex arguments:
| In[3]:= |
|
| Out[3]= |
|
Evaluate to high precision:
| In[4]:= |
|
| Out[4]= |
|
The precision of the output tracks the precision of the input:
| In[5]:= |
|
| Out[5]= |
|
Simple exact results are generated automatically:
| In[6]:= |
|
| Out[6]= |
|
| In[7]:= |
|
| Out[7]= |
|
BulirschEL2 threads elementwise over lists:
| In[8]:= |
|
| Out[8]= |
|
Series expansion of BulirschEL2 at the origin:
| In[9]:= |
|
| Out[9]= |
|
Distance along a meridian of the Earth:
| In[10]:= |
![With[{a = UnitConvert[GeodesyData["ITRF00", "SemimajorAxis"]], e = GeodesyData["ITRF00", "Eccentricity"], \[Phi] = 23 \[Degree]},
a (1 - e^2) ResourceFunction["BulirschEL2"][Tan[\[Phi]], 1 - e^2, 1, 1 + e^2]]](https://www.wolframcloud.com/obj/resourcesystem/images/5d1/5d11b272-8b45-495f-8f67-7a8df7be2e37/7a25b4e6545bd719.png)
|
| Out[10]= |
|
Compare with the result of GeoDistance:
| In[11]:= |
|
| Out[11]= |
|
Calculate the surface area of a triaxial ellipsoid:
| In[12]:= |
![area[a_, b_, c_] := 2 \[Pi] (c^2 + (a^2 b)/Sqrt[a^2 - c^2]
ResourceFunction["BulirschEL2"][Sqrt[a^2 - c^2]/c, (
c^2 (a^2 - b^2))/(b^2 (a^2 - c^2)), 1, c^2/b^2])](https://www.wolframcloud.com/obj/resourcesystem/images/5d1/5d11b272-8b45-495f-8f67-7a8df7be2e37/27299bde9f7b9bff.png)
|
The area of an ellipsoid with semiaxes 3, 2, 1:
| In[13]:= |
|
| Out[13]= |
|
Use RegionMeasure to calculate the surface area of the ellipsoid:
| In[14]:= |
|
| Out[14]= |
|
Parametrization of a Mylar balloon (two flat sheets of plastic sewn together at their circumference and then inflated):
| In[15]:= |
![x[u_, v_] := Sqrt[(1 - u^2)/(1 + u^2)] Cos[v];
y[u_, v_] := Sqrt[(1 - u^2)/(1 + u^2)] Sin[v];
z[u_, v_] := ResourceFunction["BulirschEL2"][Sqrt[2] u/Sqrt[1 - u^2], 1/2, 1/
Sqrt[2], 0];](https://www.wolframcloud.com/obj/resourcesystem/images/5d1/5d11b272-8b45-495f-8f67-7a8df7be2e37/3cfb6e8f140757f1.png)
|
Plot the resulting balloon:
| In[16]:= |
|
| Out[16]= |
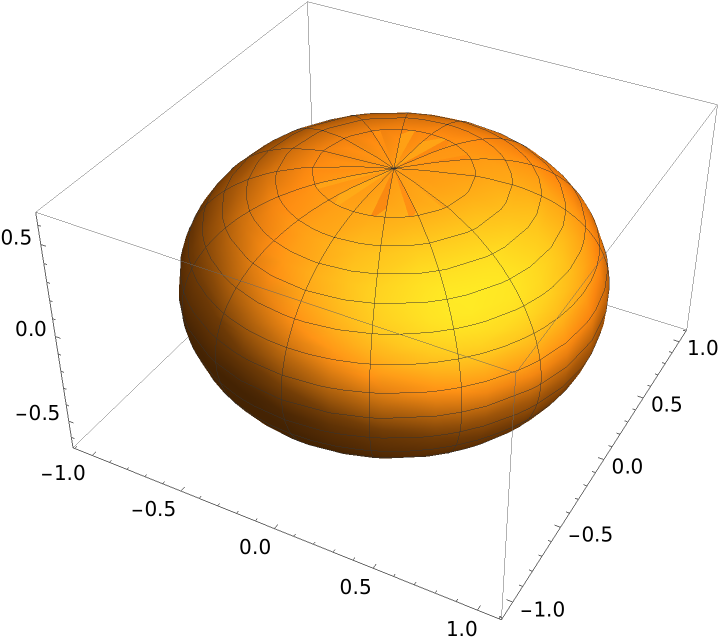
|
Both incomplete and complete cases of EllipticE can be expressed in terms of BulirschEL2:
| In[17]:= |
|
| Out[17]= |
|
| In[18]:= |
|
| Out[18]= |
|
EllipticK and EllipticF can be expressed in terms of BulirschEL2:
| In[19]:= |
|
| Out[19]= |
|
| In[20]:= |
|
| Out[20]= |
|
BulirschEL2 can be used to represent linear combinations of elliptic integrals of the first and second kinds:
| In[21]:= |
![With[{a = 4, b = 5, \[Phi] = \[Pi]/5, m = 2/3}, N[{a EllipticF[\[Phi], m] + b EllipticE[\[Phi], m], ResourceFunction["BulirschEL2"][Tan[\[Phi]], 1 - m, a + b, a + b (1 - m)]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/5d1/5d11b272-8b45-495f-8f67-7a8df7be2e37/0b4ad83f1e28fd7d.png)
|
| Out[21]= |
|
| In[22]:= |
![With[{a = 4, b = 5, m = 2/3}, N[{a EllipticK[m] + b EllipticE[m], ResourceFunction["BulirschEL2"][\[Infinity], 1 - m, a + b, a + b (1 - m)]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/5d1/5d11b272-8b45-495f-8f67-7a8df7be2e37/6d899f11c89924a8.png)
|
| Out[22]= |
|
Magnetic field lines of a ring current in cylindrical coordinates:
| In[23]:= |
![With[{R = 1},
StreamPlot[{(2 z)/(r R ((r - R)^2 + z^2) Sqrt[(r + R)^2 + z^2])
ResourceFunction["BulirschEL2"][\[Infinity], 1 - (4 r R)/((r + R)^2 + z^2), 2 r R, 2 r R ((4 r R)/((r + R)^2 + z^2) - 1)], 2/(R ((r - R)^2 + z^2) Sqrt[(r + R)^2 + z^2])
ResourceFunction["BulirschEL2"][\[Infinity], 1 - (4 r R)/((r + R)^2 + z^2), 2 R (R - r), 2 R (r + R) (1 - (4 r R)/((r + R)^2 + z^2))]}, {r, -(3/2), 3/
2}, {z, -1, 1}, {AspectRatio -> Automatic, PlotLegends -> Placed[Automatic, Right], StreamPoints -> Fine, StreamScale -> None}]]](https://www.wolframcloud.com/obj/resourcesystem/images/5d1/5d11b272-8b45-495f-8f67-7a8df7be2e37/44b87500cb40fd4e.png)
|
| Out[23]= |
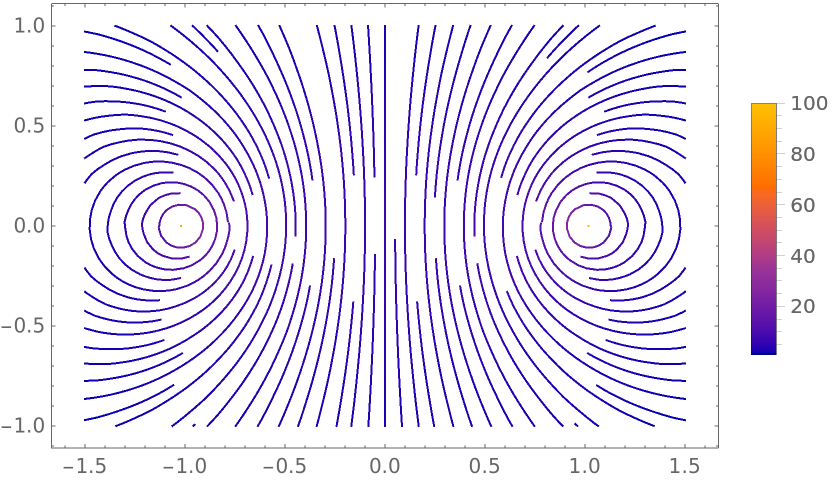
|
Wolfram Language 12.3 (May 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License