Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BulirschEL

Source Notebook

Evaluate Bulirsch's general incomplete elliptic integral

Contributed by: Jan Mangaldan

ResourceFunction["BulirschEL"][x,m,p,a,b]

gives Bulirsch's general incomplete elliptic integral .

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
Bulirsch’s general incomplete elliptic integral is defined as .
When x=∞, ResourceFunction["BulirschEL"] is referred to as a complete integral.
Argument conventions for elliptic integrals are discussed in "Elliptic Integrals and Elliptic Functions".
For certain special arguments, ResourceFunction["BulirschEL"] automatically evaluates to exact values.
ResourceFunction["BulirschEL"] can be evaluated to arbitrary precision.
ResourceFunction["BulirschEL"] automatically threads over lists.

Examples

Basic Examples (1) 

Evaluate numerically:

In[1]:=
ResourceFunction["BulirschEL"][3.4, 0.1, -4.1, 1.2, 1.1]
Out[1]=
In[2]:=
ResourceFunction["BulirschEL"][\[Infinity], 0.1, -4.1, 1.2, 1.1]
Out[2]=

Scope (5) 

Evaluate numerically for complex arguments:

In[3]:=
ResourceFunction["BulirschEL"][-1.9, 1 - 2. I, 2.5 + I, 0.6, 0.7]
Out[3]=

Evaluate to high precision:

In[4]:=
ResourceFunction["BulirschEL"][9/8, 1/2, -2.`30, 3, 4]
Out[4]=

The precision of the output tracks the precision of the input:

In[5]:=
ResourceFunction["BulirschEL"][9/8, 1/2, -2.000000000000000000000, 3, 4]
Out[5]=

Simple exact results are generated automatically:

In[6]:=
ResourceFunction["BulirschEL"][0, m, p, a, b]
Out[6]=
In[7]:=
ResourceFunction["BulirschEL"][x, {0, 1}, 1/2, 1, 1/2]
Out[7]=

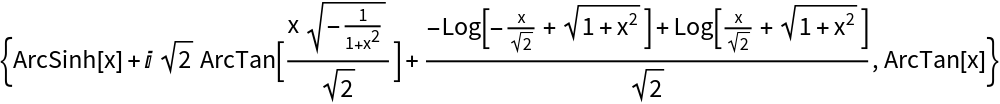
BulirschEL threads elementwise over lists:

In[8]:=
ResourceFunction["BulirschEL"][{0.2, 0.3, 0.7}, 0.9, 2.4, 1/5, 1/3]
Out[8]=

Series expansion of BulirschEL at the origin:

In[9]:=
Series[ResourceFunction["BulirschEL"][z, m, p, a, b], {z, 0, 5}]
Out[9]=

Properties and Relations (2) 

All incomplete elliptic integrals can be expressed in terms of BulirschEL:

In[10]:=
With[{\[Phi] = \[Pi]/5, m = 2/3}, N[{EllipticF[\[Phi], m], ResourceFunction["BulirschEL"][Tan[\[Phi]], 1 - m, 1, 1, 1]}]]
Out[10]=
In[11]:=
With[{\[Phi] = \[Pi]/5, m = 2/3}, N[{EllipticE[\[Phi], m], ResourceFunction["BulirschEL"][Tan[\[Phi]], 1 - m, 1, 1, 1 - m]}]]
Out[11]=
In[12]:=
With[{n = 4/5, \[Phi] = \[Pi]/5, m = 2/3}, N[{EllipticPi[n, \[Phi], m], ResourceFunction["BulirschEL"][Tan[\[Phi]], 1 - m, 1 - n, 1, 1]}]]
Out[12]=

Linear combinations of incomplete elliptic integrals can be expressed in terms of BulirschEL:

In[13]:=
With[{\[Phi] = \[Pi]/5, m = 2/3, a = 4, b = 5}, N[{a EllipticF[\[Phi], m] + b EllipticE[\[Phi], m], ResourceFunction["BulirschEL"][Tan[\[Phi]], 1 - m, 1, a + b, a + b (1 - m)]}]]
Out[13]=
In[14]:=
With[{n = 4/5, \[Phi] = \[Pi]/5, m = 2/3, a = 4, b = 5}, N[{a EllipticF[\[Phi], m] + b EllipticPi[n, \[Phi], m], ResourceFunction["BulirschEL"][Tan[\[Phi]], 1 - m, 1 - n, a + b, a (1 - n) + b]}]]
Out[14]=

Requirements

Wolfram Language 12.3 (May 2021) or above

Version History

  • 1.0.0 – 06 July 2021

Source Metadata

  • Citation:
    • Bulirsch R., "Numerical calculation of elliptic integrals and elliptic functions." Numerische Mathematik, vol. 7, no. 1, 78-90, 1965. DOI: 10.1007/BF01397975
    • Bulirsch R., "An extension of the Bartky-transformation to incomplete elliptic integrals of the third kind." Numerische Mathematik, vol. 13, no. 3, 266-284, 1969. DOI: 10.1007/BF02167558
    • Bulirsch R., "Numerical calculation of elliptic integrals and elliptic functions. III." Numerische Mathematik, vol. 13, no. 4, 305-315, 1969. DOI: 10.1007/BF02165405
    • Fukushima T., Ishizaki H., "Numerical computation of incomplete elliptic integrals of a general form." Celestial Mechanics and Dynamical Astronomy, vol. 59, 237-251, 1994. DOI: 10.1007/BF00692874

Related Resources

Author Notes

Requires 12.3 or later.
The form of the second argument was changed from the original definition used by Bulirsch, so that BulirschEL uses the parameter m=k2 instead of the modulus k. This conforms with Mathematica's choice to use the parameter in the built-in elliptic integrals and functions.

License Information