Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BresenhamPoints

Source Notebook

Calculate integer 2D point locations along a line using Bresenham's method

Contributed by: Flip Phillips (https://flipphillips.com)

ResourceFunction["BresenhamPoints"][p1,p2]

computes integer point locations along the line from p1 to p2.

Details

p1 and p2 are 2D points with integer coordinates.
The algorithm for these computations is known as Bresenham's method.
ResourceFunction["BresenhamPoints"][{p1,p2}] and ResourceFunction["BresenhamPoints"][Line[{p1,p2}]] are equivalent to ResourceFunction["BresenhamPoints"][p1,p2].

Examples

Basic Examples (1) 

Compute the points on the line from {2,3} to {7,9}:

In[1]:=
ResourceFunction["BresenhamPoints"][{2, 3}, {7, 9}]
Out[1]=

Scope (1) 

Use BresenhamPoints on a Line object:

In[2]:=
ResourceFunction["BresenhamPoints"][Line[{{11, 10}, {42, 67}}]]
Out[2]=

Applications (2) 

Visualize a line and its corresponding Bresenham points together:

In[3]:=
With[{l = Line[{{11, 10}, {67, 42}}]}, Graphics[{{LightGray, l}, {AbsolutePointSize[4], Point[ResourceFunction["BresenhamPoints"][l]]}}]]
Out[3]=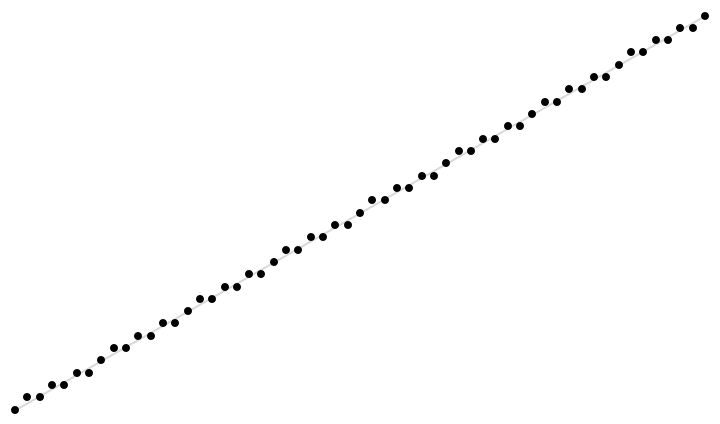

Use Raster to visualize the Bresenham points:

In[4]:=
With[{l = {{11, 10}, {67, 42}}}, bp = ResourceFunction["BresenhamPoints"][l]; Graphics[Raster[ Transpose@ Map[1 - Boole[MemberQ[bp, #]] &, CoordinateBoundsArray[Transpose[l]], {2}], l + {-1/2, 1/2}]]]
Out[4]=

Neat Examples (1) 

Extract points from an image along an arbitrary line:

In[5]:=
l = Line[{{34, 10}, {92, 120}}];
In[6]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/932ba9ac-644d-4108-9419-d5c098d06328"]
Out[6]=
In[7]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/de5cba17-6df2-4b8e-bf9d-bd67084eacdb"]
Out[7]=

Publisher

Flip Phillips

Version History

  • 1.0.0 – 16 August 2021

Source Metadata

  • Citation:
    • Bresenham, J.E., "Algorithm for computer control of a digital plotter." IBM Systems Journal, vol. 4, no. 1, 25–30, 1965. DOI: 10.1147/sj.41.0025.

Author Notes

There have been many enhancements and extensions to Bresenham's original 1963 work that compute and diffuse the residual error in different ways. Additionally, there are several extensions into higher dimensions. This is an implementation of the original algorithm.

License Information