Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the branchial hypergraph of a graph
ResourceFunction["BranchialHypergraph"][g] computes the branchial hypergraph of a graph g. | |
ResourceFunction["BranchialHypergraph"][g,n] computes the branchial hypergraph of a graph g up to the nth level of ancestry. |
| "IncludeUnary" | False | whether to include unary hyperedges |
Compute branchial hyperedges of a simple graph:
| In[1]:= | ![ResourceFunction["BranchialHypergraph"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{$CellContext`i, $CellContext`a, $CellContext`e, $CellContext`b, $CellContext`c, $CellContext`d}, {{{1, 2}, {2, 3}, {1,
4}, {4, 5}, {5, 6}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{{0.4767312946227961, 2.8603877677367766`}, {0., 1.9069251784911843`}}, {{0.4767312946227961, 2.8603877677367766`}, {0.9534625892455922, 1.9069251784911843`}}, {{0., 1.9069251784911843`}, {0., 0.9534625892455921}}, {{0.9534625892455922, 1.9069251784911843`}, {0.9534625892455922, 0.9534625892455921}}, {{0.9534625892455922, 0.9534625892455921}, {0.9534625892455922, 0.}}}, 0.029229881084280332`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{0.4767312946227961, 2.8603877677367766}, 0.029229881084280332], InsetBox["i", Offset[{2, 2}, {0.5059611757070764, 2.8896176488210568}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 1.9069251784911843}, 0.029229881084280332], InsetBox["a", Offset[{2, 2}, {0.029229881084280332, 1.9361550595754646}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.9534625892455921}, 0.029229881084280332], InsetBox["e", Offset[{2, 2}, {0.029229881084280332, 0.9826924703298725}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.9534625892455922, 1.9069251784911843}, 0.029229881084280332], InsetBox["b", Offset[{2, 2}, {0.9826924703298726, 1.9361550595754646}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.9534625892455922, 0.9534625892455921}, 0.029229881084280332], InsetBox["c", Offset[{2, 2}, {0.9826924703298726, 0.9826924703298725}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.9534625892455922, 0.}, 0.029229881084280332], InsetBox["d", Offset[{2, 2}, {0.9826924703298726, 0.029229881084280332}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{100.59877093734426`, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/3b1/3b13a20a-7932-4513-8986-28f655c6a82e/1aa5cd022d3ca6b7.png) |
| Out[1]= |
Branchial hypergraph of a mixed graph:
| In[2]:= | ![ResourceFunction["BranchialHypergraph"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5}, {{{1, 2}, {1, 4}, {3, 5}}, {{1, 3}, {3, 4}}}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium],
{Arrowheads[0.], ArrowBox[{{2.123724619186534, 0.2848465012502784}, {
1.0246020231662252`, 0.28468259702878873`}}, 0.031290867382760074`]}, ArrowBox[{{2.123724619186534, 0.2848465012502784}, {
3.147903408145563, 0.}}, 0.031290867382760074`], ArrowBox[{{2.123724619186534, 0.2848465012502784}, {
1.5742315378161784`, 0.9655937588020892}}, 0.031290867382760074`],
{Arrowheads[0.], ArrowBox[{{1.0246020231662252`, 0.28468259702878873`}, {
1.5742315378161784`, 0.9655937588020892}}, 0.031290867382760074`]}, ArrowBox[{{1.0246020231662252`, 0.28468259702878873`}, {0., 0.00016831547416262804`}}, 0.031290867382760074`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{2.123724619186534, 0.2848465012502784}, 0.031290867382760074], InsetBox["1", Offset[{2, 2}, {2.1550154865692943, 0.31613736863303843}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{3.147903408145563, 0.}, 0.031290867382760074], InsetBox["2", Offset[{2, 2}, {3.179194275528323, 0.031290867382760074}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.0246020231662252, 0.28468259702878873}, 0.031290867382760074], InsetBox["3", Offset[{2, 2}, {1.0558928905489853, 0.31597346441154883}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.5742315378161784, 0.9655937588020892}, 0.031290867382760074], InsetBox["4", Offset[{2, 2}, {1.6055224051989385, 0.9968846261848493}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.00016831547416262804}, 0.031290867382760074], InsetBox["5", Offset[{2, 2}, {0.031290867382760074, 0.0314591828569227}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{254.3203125, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/3b1/3b13a20a-7932-4513-8986-28f655c6a82e/783971c106edb1ce.png) |
| Out[2]= |
Specify the maximum level of ancestry:
| In[3]:= | ![ResourceFunction["BranchialHypergraph"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5}, {{{1, 2}, {1, 4}, {3, 5}}, {{1, 3}, {3, 4}}}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium],
{Arrowheads[0.], ArrowBox[{{2.123724619186534, 0.2848465012502784}, {
1.0246020231662252`, 0.28468259702878873`}}, 0.031290867382760074`]}, ArrowBox[{{2.123724619186534, 0.2848465012502784}, {
3.147903408145563, 0.}}, 0.031290867382760074`], ArrowBox[{{2.123724619186534, 0.2848465012502784}, {
1.5742315378161784`, 0.9655937588020892}}, 0.031290867382760074`],
{Arrowheads[0.], ArrowBox[{{1.0246020231662252`, 0.28468259702878873`}, {
1.5742315378161784`, 0.9655937588020892}}, 0.031290867382760074`]}, ArrowBox[{{1.0246020231662252`, 0.28468259702878873`}, {0., 0.00016831547416262804`}}, 0.031290867382760074`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{2.123724619186534, 0.2848465012502784}, 0.031290867382760074], InsetBox["1", Offset[{2, 2}, {2.1550154865692943, 0.31613736863303843}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{3.147903408145563, 0.}, 0.031290867382760074], InsetBox["2", Offset[{2, 2}, {3.179194275528323, 0.031290867382760074}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.0246020231662252, 0.28468259702878873}, 0.031290867382760074], InsetBox["3", Offset[{2, 2}, {1.0558928905489853, 0.31597346441154883}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.5742315378161784, 0.9655937588020892}, 0.031290867382760074], InsetBox["4", Offset[{2, 2}, {1.6055224051989385, 0.9968846261848493}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.00016831547416262804}, 0.031290867382760074], InsetBox["5", Offset[{2, 2}, {0.031290867382760074, 0.0314591828569227}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{254.3203125, Automatic}]\), 1]](https://www.wolframcloud.com/obj/resourcesystem/images/3b1/3b13a20a-7932-4513-8986-28f655c6a82e/11ab21796cd57606.png) |
| Out[3]= |
The branchial hypergraph of any undirected graph is empty:
| In[4]:= |
| Out[4]= |
Generate a simple string substitution multiway system with the resource function MultiwaySystem and compute its branchial hypergraph:
| In[5]:= |
| Out[5]= | 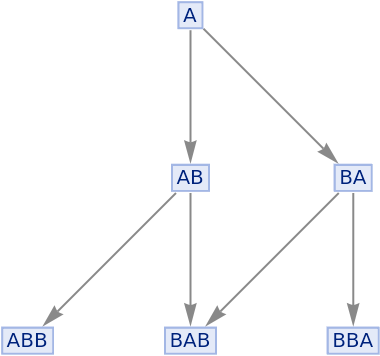 |
| In[6]:= |
| Out[6]= |
Use the resource function WolframModelPlot to visualize the branchial hypergraph:
| In[7]:= | ![ResourceFunction["WolframModelPlot"][
ResourceFunction["BranchialHypergraph"]@\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{"A", "AB", "BA", "ABB", "BAB", "BBA"}, {{{1, 2}, {1, 3}, {2, 4}, {2, 5}, {3, 5}, {3, 6}}, Null}, {EdgeStyle -> {
Directive[{
Hue[0.75, 0, 0.35],
Dashing[None],
AbsoluteThickness[1]}]}, PerformanceGoal -> "Quality", VertexShapeFunction -> {Text[
Framed[
Style[
FunctionRepository`$d565908159ef4f95abe6d42d3d3ed1a6`stripMetadata[#2],
Hue[0.62, 1, 0.48]], Background -> Directive[
Opacity[0.2],
Hue[0.62, 0.45, 0.87]], FrameMargins -> {{2, 2}, {0, 0}}, RoundingRadius -> 0, FrameStyle -> Directive[
Opacity[0.5],
Hue[0.62, 0.52, 0.82]]], #, {0, 0}]& }}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Arrowheads[Medium],
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
Directive[{
Hue[0.75, 0, 0.35],
Dashing[None],
AbsoluteThickness[1]}],
ArrowBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}],
ArrowBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}],
ArrowBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}],
ArrowBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}],
ArrowBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}],
ArrowBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
InsetBox[
FormBox[
FrameBox[
StyleBox["\"A\"",
Hue[0.62, 1, 0.48], StripOnInput -> False], Background -> Directive[
Opacity[0.2],
Hue[0.62, 0.45, 0.87]], FrameMargins -> {{2, 2}, {0, 0}}, RoundingRadius -> 0, FrameStyle -> Directive[
Opacity[0.5],
Hue[0.62, 0.52, 0.82]], StripOnInput -> False], TraditionalForm], {0.,
2.},
ImageScaled[{
Rational[1, 2],
Rational[1, 2]}]], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
FormBox[
FrameBox[
StyleBox["\"AB\"",
Hue[0.62, 1, 0.48], StripOnInput -> False], Background -> Directive[
Opacity[0.2],
Hue[0.62, 0.45, 0.87]], FrameMargins -> {{2, 2}, {0, 0}}, RoundingRadius -> 0, FrameStyle -> Directive[
Opacity[0.5],
Hue[0.62, 0.52, 0.82]], StripOnInput -> False], TraditionalForm], {0.,
1.},
ImageScaled[{
Rational[1, 2],
Rational[1, 2]}]], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
InsetBox[
FormBox[
FrameBox[
StyleBox["\"BA\"",
Hue[0.62, 1, 0.48], StripOnInput -> False], Background -> Directive[
Opacity[0.2],
Hue[0.62, 0.45, 0.87]], FrameMargins -> {{2, 2}, {0, 0}}, RoundingRadius -> 0, FrameStyle -> Directive[
Opacity[0.5],
Hue[0.62, 0.52, 0.82]], StripOnInput -> False], TraditionalForm], {1.,
1.},
ImageScaled[{
Rational[1, 2],
Rational[1, 2]}]], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
InsetBox[
FormBox[
FrameBox[
StyleBox["\"ABB\"",
Hue[0.62, 1, 0.48], StripOnInput -> False], Background -> Directive[
Opacity[0.2],
Hue[0.62, 0.45, 0.87]], FrameMargins -> {{2, 2}, {0, 0}}, RoundingRadius -> 0, FrameStyle -> Directive[
Opacity[0.5],
Hue[0.62, 0.52, 0.82]], StripOnInput -> False], TraditionalForm], {-1., 0.},
ImageScaled[{
Rational[1, 2],
Rational[1, 2]}]], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
InsetBox[
FormBox[
FrameBox[
StyleBox["\"BAB\"",
Hue[0.62, 1, 0.48], StripOnInput -> False], Background -> Directive[
Opacity[0.2],
Hue[0.62, 0.45, 0.87]], FrameMargins -> {{2, 2}, {0, 0}}, RoundingRadius -> 0, FrameStyle -> Directive[
Opacity[0.5],
Hue[0.62, 0.52, 0.82]], StripOnInput -> False], TraditionalForm], {0.,
0.},
ImageScaled[{
Rational[1, 2],
Rational[1, 2]}]], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
InsetBox[
FormBox[
FrameBox[
StyleBox["\"BBA\"",
Hue[0.62, 1, 0.48], StripOnInput -> False], Background -> Directive[
Opacity[0.2],
Hue[0.62, 0.45, 0.87]], FrameMargins -> {{2, 2}, {0, 0}}, RoundingRadius -> 0, FrameStyle -> Directive[
Opacity[0.5],
Hue[0.62, 0.52, 0.82]], StripOnInput -> False], TraditionalForm], {1.,
0.},
ImageScaled[{
Rational[1, 2],
Rational[1, 2]}]], "DynamicName", BoxID -> "VertexID$6"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{-7.105427357601002*^-15, 138.08203125}, {-67.08203125, 62.}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{138.08203125, Automatic},
ImageSizeRaw->{190., 181.}]\), Sequence @@ ResourceFunction["WolframPhysicsProjectStyleData"][
"BranchialGraph"]["Options"], VertexLabels -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/3b1/3b13a20a-7932-4513-8986-28f655c6a82e/16e4a7b10dfc0f57.png) |
| Out[7]= | 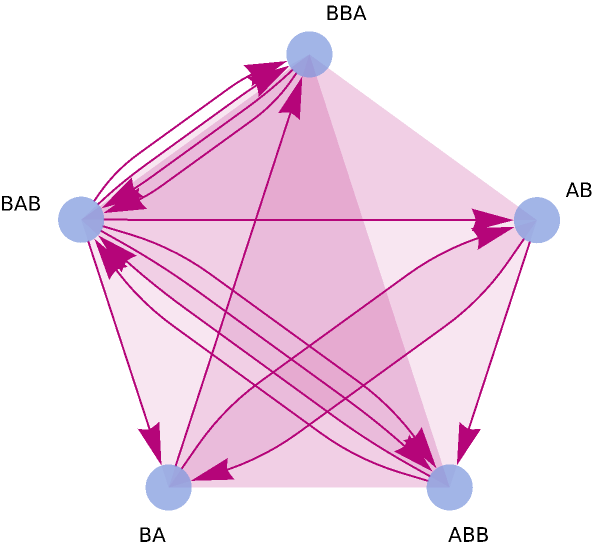 |
Include unary hyperedges:
| In[8]:= | ![ResourceFunction["BranchialHypergraph"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{$CellContext`i, $CellContext`a, $CellContext`e, $CellContext`b, $CellContext`c, $CellContext`d}, {{{1, 2}, {2, 3}, {1,
4}, {4, 5}, {5, 6}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{{0.4767312946227961, 2.8603877677367766`}, {0., 1.9069251784911843`}}, {{0.4767312946227961, 2.8603877677367766`}, {0.9534625892455922, 1.9069251784911843`}}, {{0., 1.9069251784911843`}, {0., 0.9534625892455921}}, {{0.9534625892455922, 1.9069251784911843`}, {0.9534625892455922, 0.9534625892455921}}, {{0.9534625892455922, 0.9534625892455921}, {0.9534625892455922, 0.}}}, 0.029229881084280332`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{0.4767312946227961, 2.8603877677367766}, 0.029229881084280332], InsetBox["i", Offset[{2, 2}, {0.5059611757070764, 2.8896176488210568}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 1.9069251784911843}, 0.029229881084280332], InsetBox["a", Offset[{2, 2}, {0.029229881084280332, 1.9361550595754646}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.9534625892455921}, 0.029229881084280332], InsetBox["e", Offset[{2, 2}, {0.029229881084280332, 0.9826924703298725}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.9534625892455922, 1.9069251784911843}, 0.029229881084280332], InsetBox["b", Offset[{2, 2}, {0.9826924703298726, 1.9361550595754646}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.9534625892455922, 0.9534625892455921}, 0.029229881084280332], InsetBox["c", Offset[{2, 2}, {0.9826924703298726, 0.9826924703298725}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.9534625892455922, 0.}, 0.029229881084280332], InsetBox["d", Offset[{2, 2}, {0.9826924703298726, 0.029229881084280332}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{100.59877093734426`, Automatic}]\), "IncludeUnary" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/3b1/3b13a20a-7932-4513-8986-28f655c6a82e/0bcfc0fc1d1e7f0b.png) |
| Out[8]= |
Recover the branchial graph from the hypergraph:
| In[9]:= | ![GraphicsRow[{
ResourceFunction[
"MultiwaySystem"][{"A" -> "AB", "A" -> "BA", "A" -> "BB"}, "A", 4, "AllStatesBranchialGraphStructure"], SimpleGraph[
UndirectedEdge @@@ ResourceFunction["BranchialHypergraph"][
ResourceFunction[
"MultiwaySystem"][{"A" -> "AB", "A" -> "BA", "A" -> "BB"}, "A", 4, "StatesGraph"], 1],
Sequence @@ ResourceFunction["WolframPhysicsProjectStyleData"][
"BranchialGraph"]["Options"]]
}, Frame -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/3b1/3b13a20a-7932-4513-8986-28f655c6a82e/24077f118cd8c9cc.png) |
| Out[9]= | 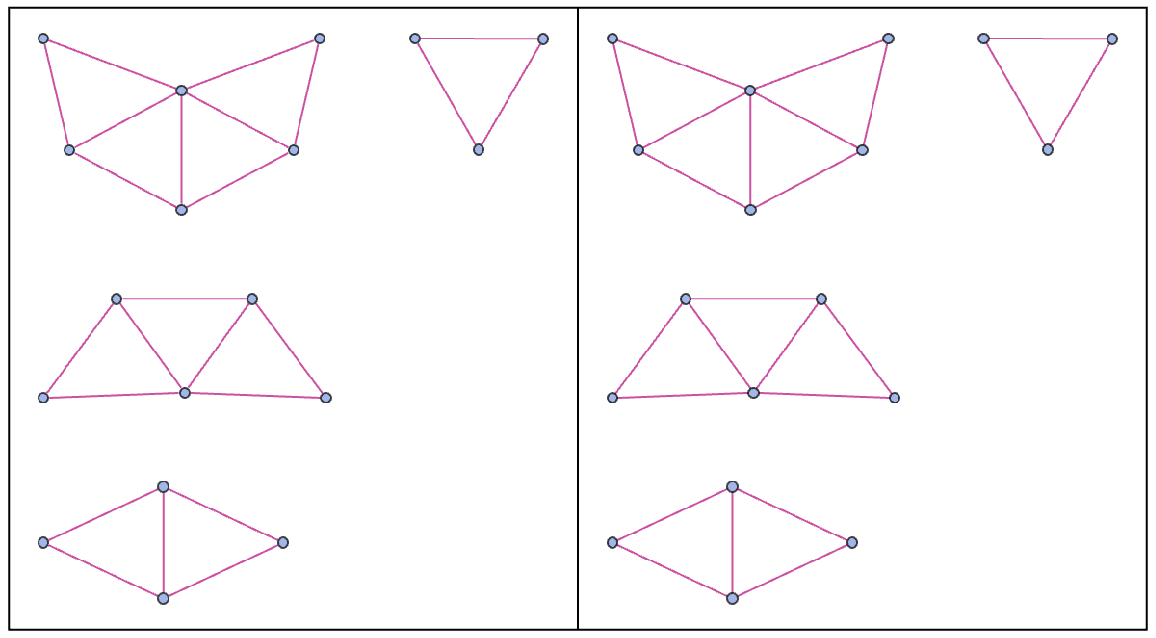 |
This work is licensed under a Creative Commons Attribution 4.0 International License