Details
ResourceFunction["BranchialGraphs"] takes the same options as
Graph.
Two vertices vj and vk are have branch-like separation if g contains a vertex vi and a pair of edges vi→vj and vi→vk.
Branch-like separation is necessary, but not sufficient, for an edge between vj and vk to appear in a branchial graph of g.
A foliation of the vertices of g is a partitioning of g-vertices into time-ordered subsets (preferably also an exact cover).
Vertices vj and vk must also satisfy a simultaneity condition, which depends on choice of a foliation.
ResourceFunction["BranchialGraphs"] takes an additional option of the form: "Foliation" → {{v1,v2,…,vn}, {vn+1,vn+2,…,vn+m}, …, {vx,vx+1,…,vx+y}}.
The default
"Foliation" lists a vertex in a subset as soon as its entire
VertexInComponent is covered by preceding subsets.
If a specified
"Foliation" lists a vertex before its entire
VertexInComponent is covered by preceding subsets, the algorithm will not give a valid result.
The positions of subsets in the foliation determine their
Keys in the output of
ResourceFunction["BranchialGraphs"].
Provided the foliation subset at time ti includes vertices vj and vk from g, then the branchial graph at time ti will have an edge between vj and vk if and only if vj and vk have branch-like separation.
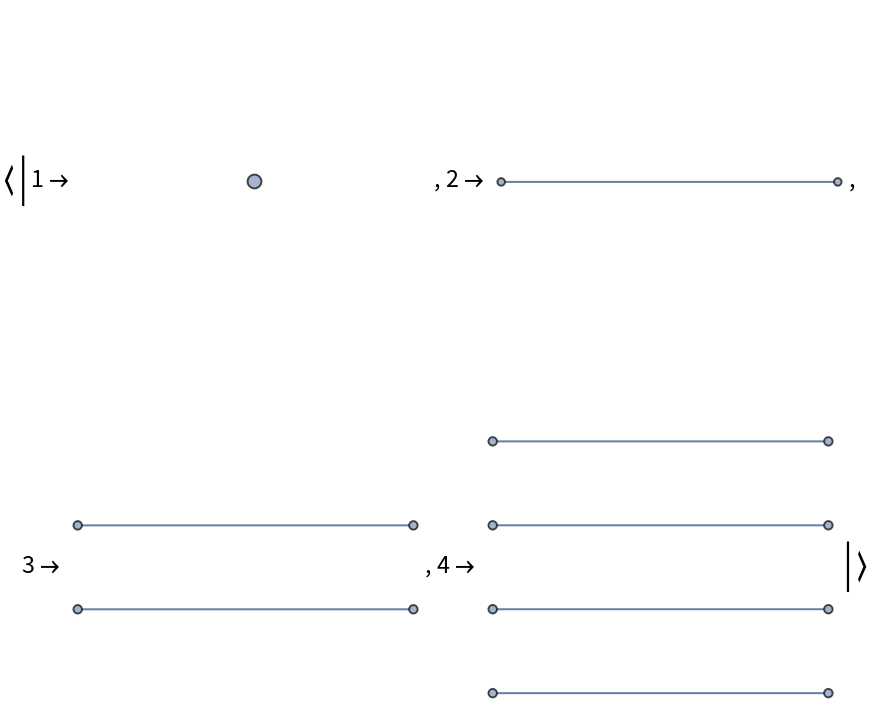
![With[{g0 = NestGraph[{# + 1, 2 #, 2 # + 1} &, 1, 5]},
Column[{Graph[g0, ImageSize -> 300], "",
Grid[Partition[
KeyValueMap[Labeled[Framed[Graph[#2, ImageSize -> 25],
FrameStyle -> LightGray], Style[#1, GrayLevel[0.6]]] &,
ResourceFunction["BranchialGraphs"][g0]], 8], Spacings -> {1, 1}]}, Alignment -> Center]]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c9e284-0d40-4e7a-a8d8-9d191a2d4a22/4c6e9ed4012d53fb.png)
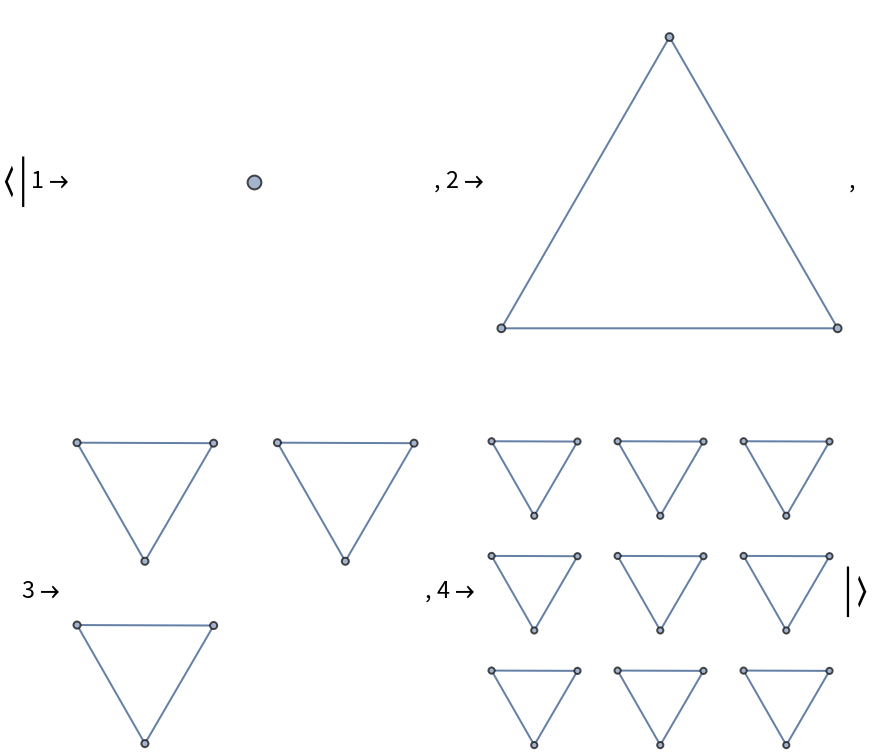
![With[{g0 = NestGraph[{# + 1, 3 #, 3 # + 1, 3 # + 2} &, 1, 4]},
Column[{Graph[g0, ImageSize -> 300], "",
Grid[Partition[
KeyValueMap[Labeled[Framed[Graph[#2, ImageSize -> 25],
FrameStyle -> LightGray], Style[#1, GrayLevel[0.6]]] &,
ResourceFunction["BranchialGraphs"][g0]], 8], Spacings -> {1, 1}]}, Alignment -> Center]]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c9e284-0d40-4e7a-a8d8-9d191a2d4a22/3a5a70a502c7436b.png)
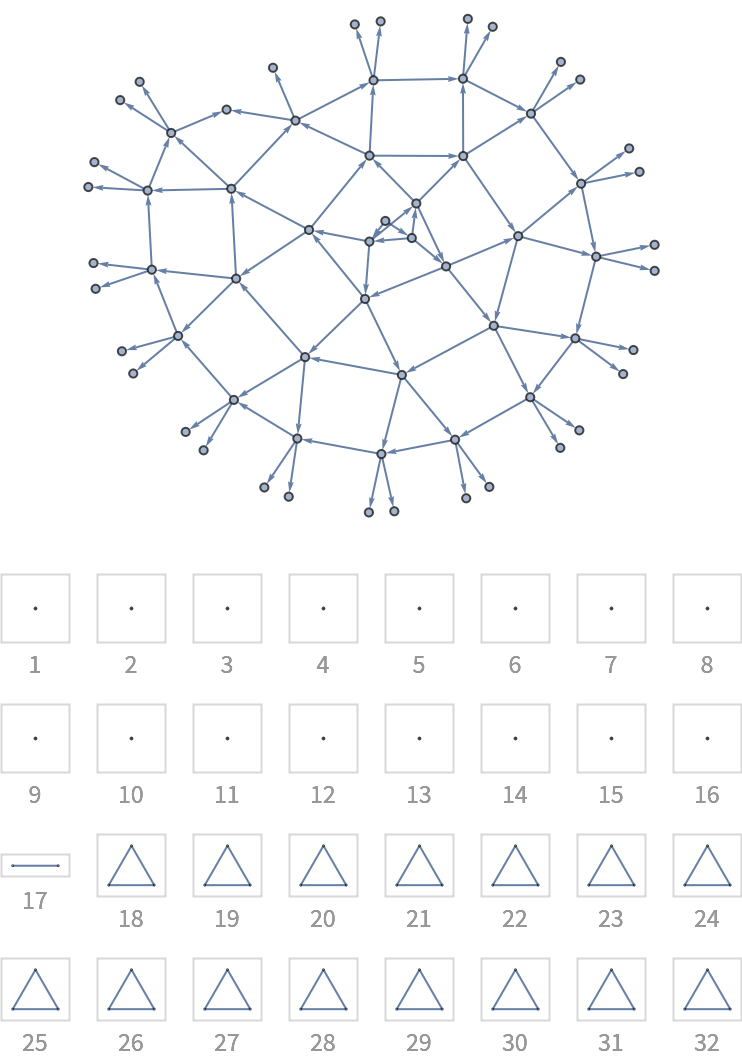
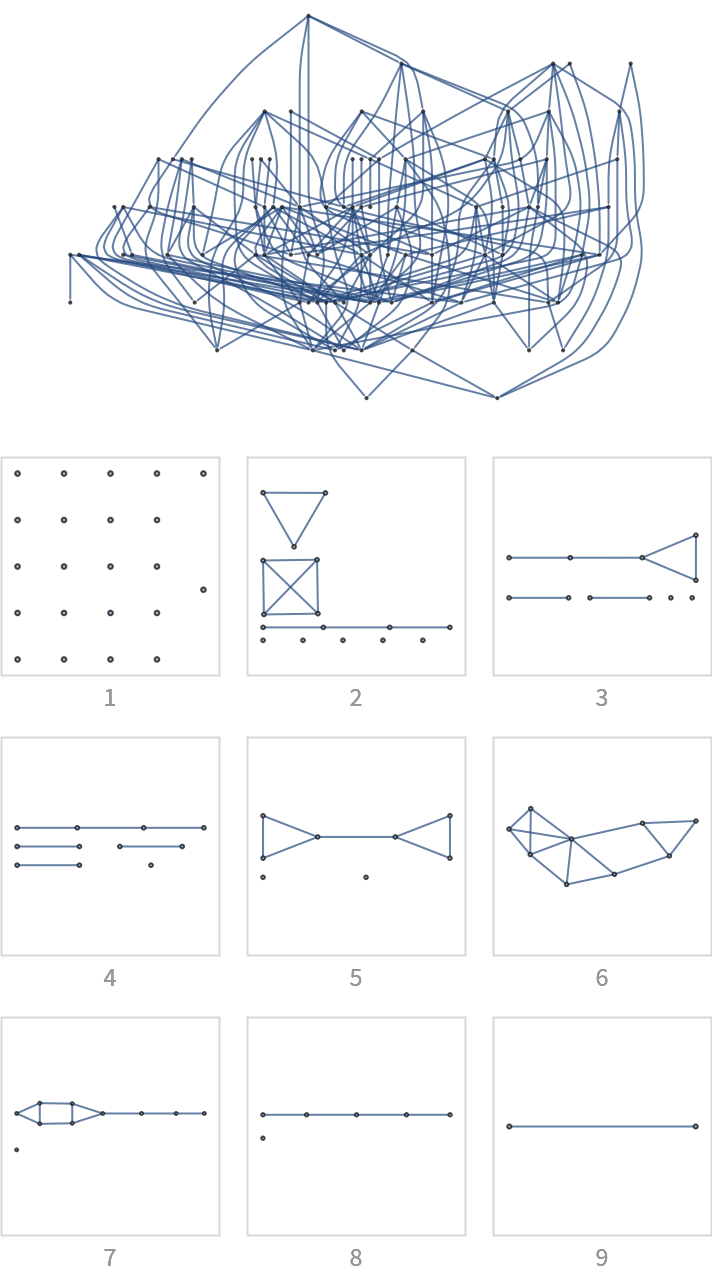
![With[{g0 = (SeedRandom[12345]; First[WeaklyConnectedGraphComponents[
DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])},
Column[{Graph[g0, ImageSize -> 300, GraphLayout -> "LayeredDigraphEmbedding", AspectRatio -> 2/3], "",
Grid[Partition[
KeyValueMap[
Labeled[Framed[Graph[#2, ImageSize -> {UpTo[100], 100}],
FrameStyle -> LightGray], Style[#1, GrayLevel[0.6]]] &,
ResourceFunction["BranchialGraphs"][g0]], 3], Spacings -> {1, 1}]}, Alignment -> Center]]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c9e284-0d40-4e7a-a8d8-9d191a2d4a22/705dd82982df1a2c.png)
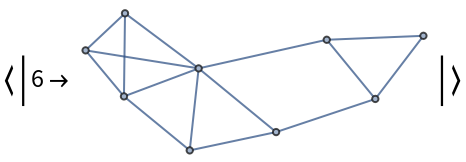
![With[{g0 = (SeedRandom[12345]; First[WeaklyConnectedGraphComponents[
DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])},
ResourceFunction["BranchialGraphs"][g0, {6}]]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c9e284-0d40-4e7a-a8d8-9d191a2d4a22/3e9107b8348532cd.png)
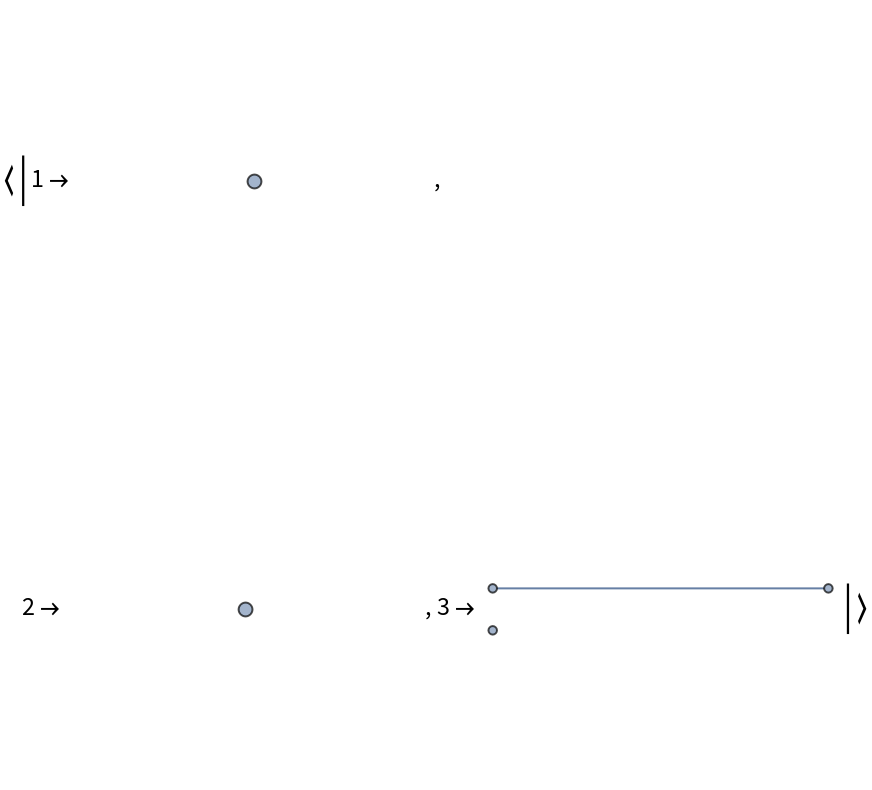
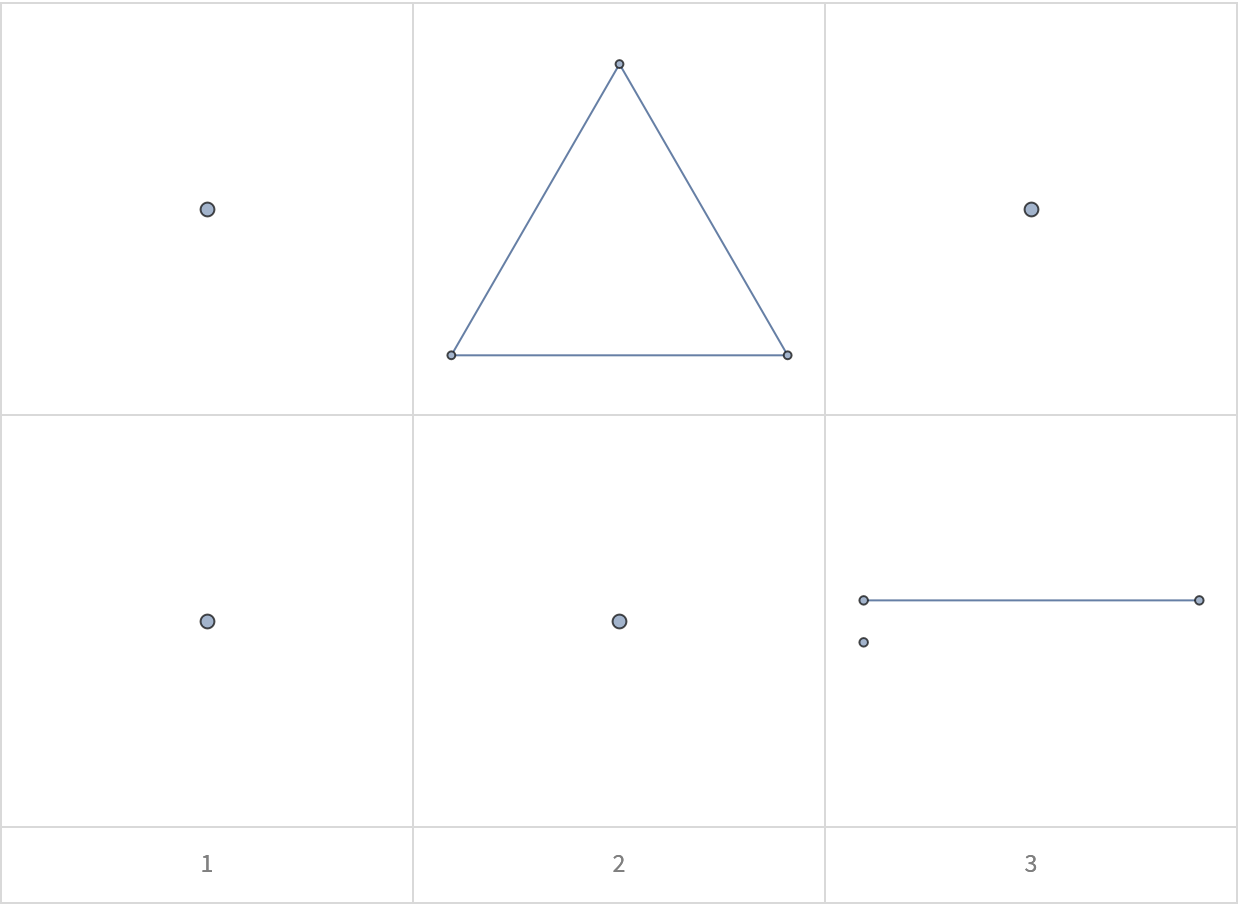
![With[{g0 = Graph[{1 -> 2, 2 -> 3, 1 -> 4, 1 -> 5}]},
Grid[{Values@ResourceFunction["BranchialGraphs"][g0],
Values@ResourceFunction["BranchialGraphs"][g0,
"Foliation" -> {{1}, {2}, {3, 4, 5}}],
Style[#, Gray] & /@ {1, 2, 3}}, Frame -> All,
Spacings -> {2, 2}, FrameStyle -> LightGray]]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c9e284-0d40-4e7a-a8d8-9d191a2d4a22/00e592b48ba271db.png)
![With[{g0 = (SeedRandom[12345]; First[WeaklyConnectedGraphComponents[
DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])},
ResourceFunction["BranchialGraphs"][g0, {6}, EdgeStyle -> Darker[Magenta],
VertexStyle -> Directive[EdgeForm[Darker@Purple], Lighter[Purple, .7]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c9e284-0d40-4e7a-a8d8-9d191a2d4a22/0d3eb30cae96cd67.png)
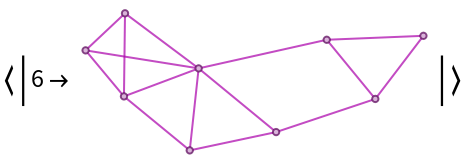
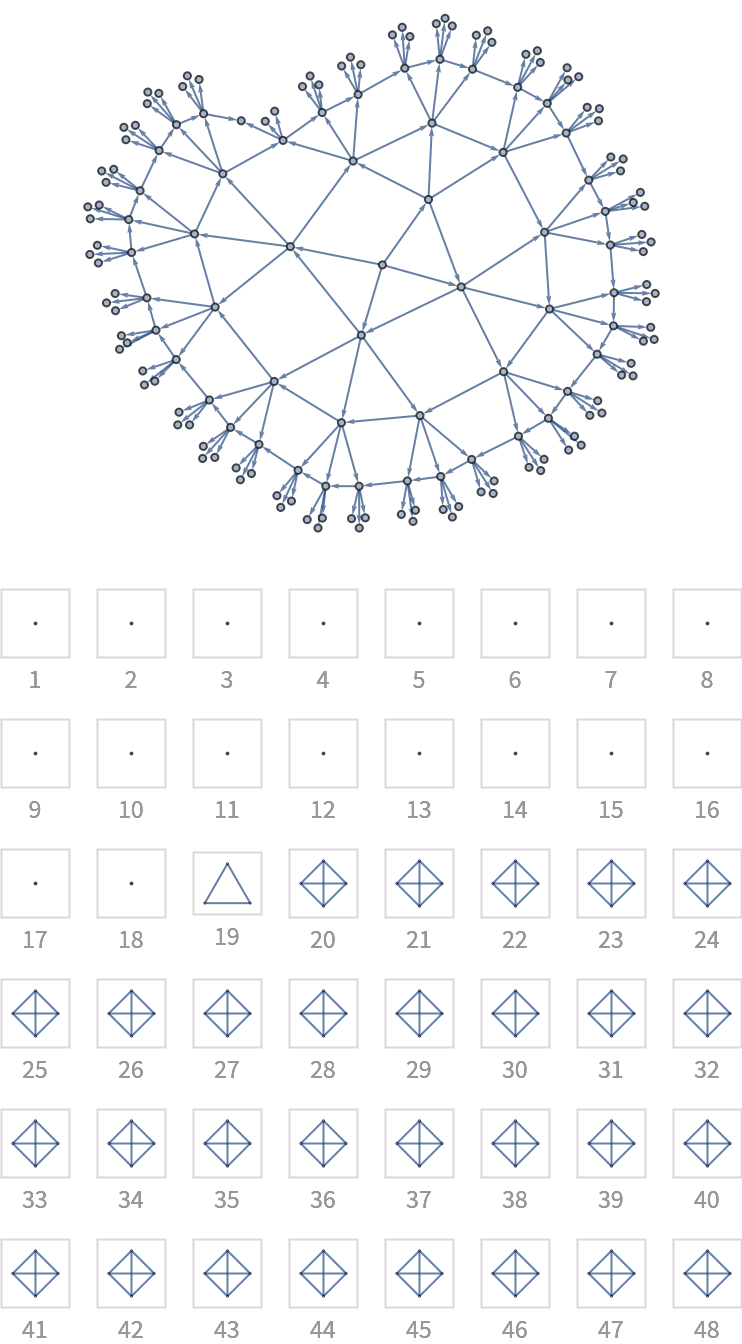
![With[{g0 = (SeedRandom[12345]; First[WeaklyConnectedGraphComponents[
DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])},
Column[{Graph[g0, ImageSize -> 300, GraphLayout -> "LayeredDigraphEmbedding", AspectRatio -> 2/3], "",
Grid[Partition[
KeyValueMap[
Labeled[Framed[Graph[#2, ImageSize -> {UpTo[100], 100}],
FrameStyle -> LightGray], Style[10 - #1, GrayLevel[0.6]]] &,
Reverse@ResourceFunction["BranchialGraphs"][ReverseGraph@g0,
"Foliation" -> Reverse[VertexList /@ Values[ResourceFunction["BranchialGraphs"][g0]]]]
], 3], Spacings -> {1, 1}]}, Alignment -> Center]]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c9e284-0d40-4e7a-a8d8-9d191a2d4a22/3ada49deee8538b9.png)
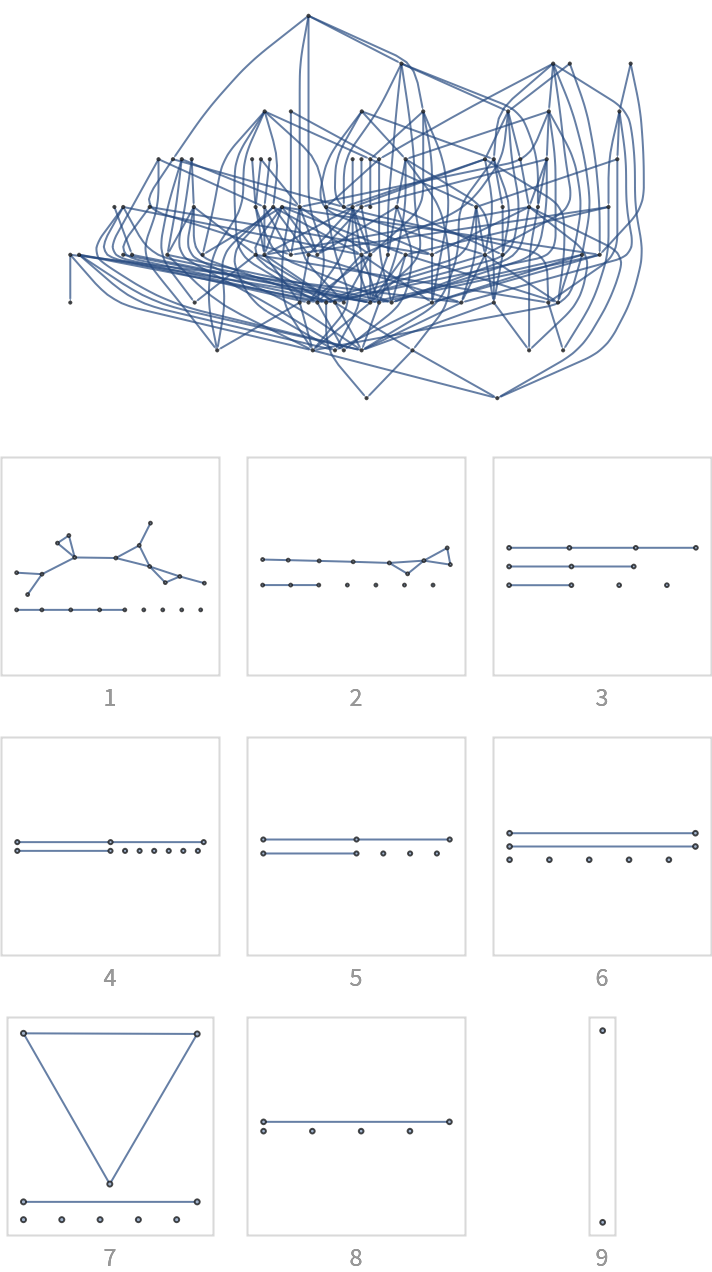
![With[{g0 = (SeedRandom[12345]; ReverseGraph@First[WeaklyConnectedGraphComponents[
DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])},
Column[{Graph[g0, ImageSize -> 300, GraphLayout -> "LayeredDigraphEmbedding", AspectRatio -> 2/3], "",
Grid[Partition[
KeyValueMap[
Labeled[Framed[Graph[#2, ImageSize -> {UpTo[100], 100}],
FrameStyle -> LightGray], Style[#1, GrayLevel[0.6]]] &,
ResourceFunction["BranchialGraphs"][g0]
], 3], Spacings -> {1, 1}]}, Alignment -> Center]]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c9e284-0d40-4e7a-a8d8-9d191a2d4a22/68b72fc1e9f973d2.png)
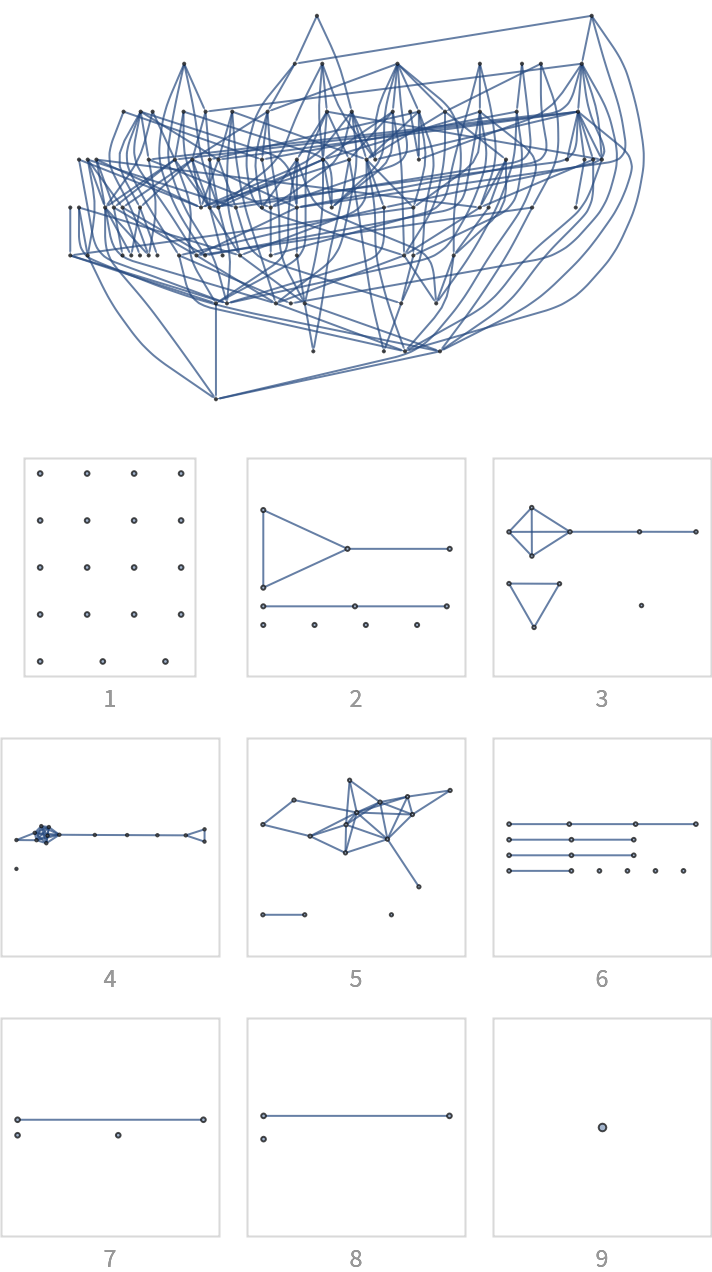
![With[{
g0 = (SeedRandom[12345]; First[WeaklyConnectedGraphComponents[
DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]]),
g1 = (SeedRandom[12345]; ReverseGraph@First[WeaklyConnectedGraphComponents[
DirectedGraph[RandomGraph[{100, 200}], "Acyclic"]]])},
Intersection @@@ Transpose[{VertexList /@ Values[ResourceFunction["BranchialGraphs"][g0]],
Reverse[
VertexList /@ Values[ResourceFunction["BranchialGraphs"][g1]]]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c9e284-0d40-4e7a-a8d8-9d191a2d4a22/5c6a924c61615f65.png)