Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BoundaryMeshUnion

Source Notebook

Merge multiple regions into a single boundary mesh

Contributed by: Louis Breton

ResourceFunction["BoundaryMeshUnion"][{region1,region2,…}]

generates an ElementMesh object that combines the boundaries of multiple regions into a single unified mesh.

ResourceFunction["BoundaryMeshUnion"][{{region1,"BoundaryMarker"→value1},{region2,"BoundaryMarker"→value2}…}]

assigns specified boundary markers (value1,value2, …) to each corresponding region.

ResourceFunction["BoundaryMeshUnion"][{{region1,"BoundaryMarker"→value1,opts1},{region2,"BoundaryMarker"→value2,opts2}…}]

generates a unified boundary ElementMesh, assigning specified boundary markers (value1,value2, …) to each corresponding region. Each optsi can include any option from Options[ToBoundaryMesh].

Details

Additional settings for each region can be provided using ResourceFunction["BoundaryMeshUnion"][{{region1,"BoundaryMarker"→value1,opts1},{region2,"BoundaryMarker"→value2,opts2}…}].
BoundaryMeshUnion merges multiple geometric regions into a single boundary mesh, enabling distinct configurations for each region.
The regioni values support any regions specification, for example {Rectangle[],Disk[]}.
The optsi can include any option from Options[ToBoundaryMesh], allowing for tailored mesh configurations. The "BoundaryMarker"→value syntax pairs a numeric value with the boundary elements of the specified region, facilitating distinct treatment in mesh-based analyses.

Examples

Basic Examples (4) 

Combine rectangular and circular boundaries:

In[1]:=
regionsWithoutMarkers = { Rectangle[{0, 0}, {10, 5}], Circle[{3, 2.5}, 1]}; Bmesh = ResourceFunction["BoundaryMeshUnion"][regionsWithoutMarkers][ "Wireframe"]
Out[3]=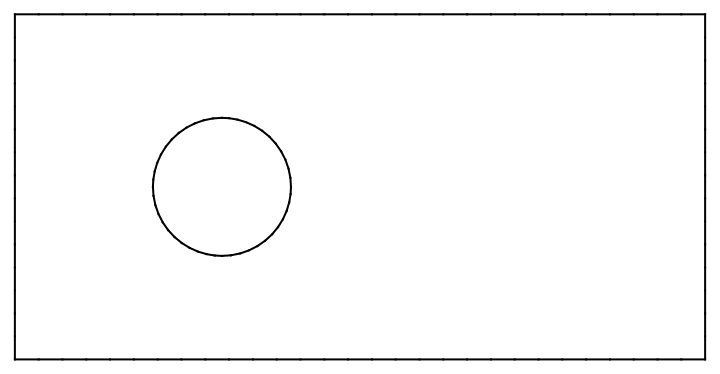

Define boundaries with custom markers:

In[4]:=
regionsMarkes = { {Rectangle[{0, 0}, {10, 5}], "BoundaryMarker" -> 1}, {Line[{{2, 2}, {5, 2}}], "BoundaryMarker" -> 2} }; Bmesh = ResourceFunction["BoundaryMeshUnion"][regionsMarkes]; (* Visualize the boundary mesh *) GraphicsRow[{Bmesh[ "Wireframe"["MeshElement" -> "PointElements", "MeshElementMarkerStyle" -> Blue]], Bmesh["Wireframe"["MeshElement" -> "BoundaryElements", "MeshElementMarkerStyle" -> Blue]]}]
Out[6]=

Define boundaries with custom markers and point inclusions:

In[7]:=
regionsMarkersOptions = { {Rectangle[{0, 0}, {10, 5}], "BoundaryMarker" -> 1}, {Line[{{2, 2}, {5, 2}}], "BoundaryMarker" -> 2 , "IncludePoints" -> {{4, 3}}}}; Bmesh = ResourceFunction["BoundaryMeshUnion"][regionsMarkersOptions]; (* Visualize the boundary mesh *) Bmesh["Wireframe"["MeshElement" -> "PointElements", "MeshElementMarkerStyle" -> Blue]]
Out[9]=

Create a mesh with custom markers and custom density:

In[10]:=
regionsWithOptions = { {Rectangle[{0, 0}, {10, 5}], "BoundaryMarker" -> 1, MaxCellMeasure -> {"Length" -> 1}}, {Disk[{5, 2.5}, 1], "BoundaryMarker" -> 2, MaxCellMeasure -> {"Length" -> 0.1}} }; mesh = NDSolve`FEM`ToElementMesh[ ResourceFunction["BoundaryMeshUnion"][regionsWithOptions], "RegionHoles" -> {{5, 2.5}}]; (* Visualize with adjusted mesh *) mesh["Wireframe"]
Out[12]=

Possible Issues (2) 

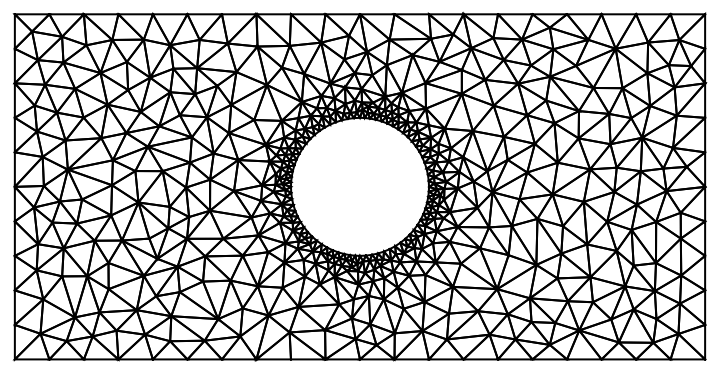Overlapping boundaries may have incorrect PointElement markings:

In[13]:=
regionsMarkes = { {Rectangle[{0, 0}, {10, 5}], "BoundaryMarker" -> 1}, {Line[{{2, 2}, {5, 2}}], "BoundaryMarker" -> 2}, {Line[{{2, 2}, {5, 3}}], "BoundaryMarker" -> 3}, {Line[{{5, 3}, {5, 2}}], "BoundaryMarker" -> 4} }; Bmesh = ResourceFunction["BoundaryMeshUnion"][regionsMarkes]
Out[14]=

Visualize the boundary mesh:

In[15]:=
GraphicsRow[{Bmesh[ "Wireframe"["MeshElement" -> "PointElements", "MeshElementMarkerStyle" -> Blue]], Bmesh["Wireframe"["MeshElement" -> "BoundaryElements", "MeshElementMarkerStyle" -> Blue]]}]
Out[15]=

Neat Examples (3) 

Solve the Laplace equation in a non-trivial geometry:

In[16]:=
<< NDSolve`FEM`; regionsWithOptions = { {Rectangle[{0, 0}, {10, 5}], "BoundaryMarker" -> 1, MaxCellMeasure -> {"Length" -> 0.5}}, {RegionUnion[Disk[{5, 2.5}, 1], Disk[{6, 2.5}, 1]], "BoundaryMarker" -> 2, MaxCellMeasure -> {"Length" -> 0.1}}}; mesh = ToElementMesh[ ResourceFunction["BoundaryMeshUnion"][regionsWithOptions], "RegionHoles" -> {{5, 2.5}}]; mesh["Wireframe"]
Out[19]=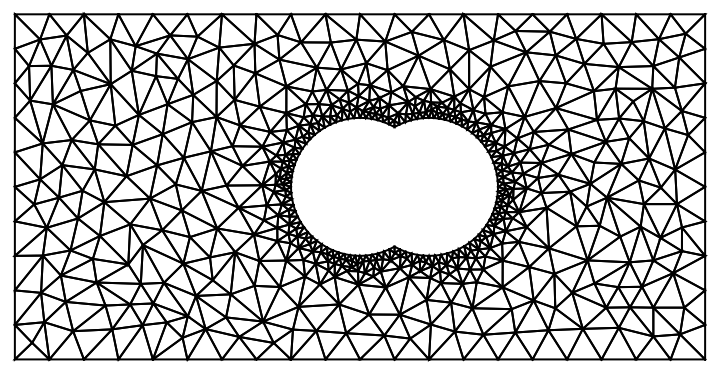

Set up boundary conditions:

In[20]:=
leqn = \!\( \*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[x, y]\)\) == 0; r1 = DirichletCondition[u[x, y] == 0, ElementMarker == 1]; r2 = DirichletCondition[u[x, y] == 1, ElementMarker == 2]; pdeC = {leqn, {r1, r2}}
Out[23]=

Solve it and visualize the result:

In[24]:=
usol = NDSolveValue[pdeC, u, {x, y} \[Element] mesh]; Plot3D[usol[x, y], {x, y} \[Element] mesh, Mesh -> None, PlotRange -> All]
Out[25]=

Publisher

Louis Breton

Version History

  • 1.0.0 – 25 October 2024

Related Resources

License Information