Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BootstrappedEstimate

Source Notebook

Perform bootstrapping of an estimator on some data

Contributed by: Sander Huisman

ResourceFunction["BootstrappedEstimate"][data,e,n]

bootstraps the data data using the estimator e with n bootstrap samples.

Details and Options

Bootstrapping involves randomly sampling elements from a dataset and calculating the estimator multiple times. The variance in the found estimator is then an indicator for the uncertainty of the estimator.
For each run (out of n), the estimator e is calculated for a randomly sampled set of elements from data (with possible repeats). This will result in n estimates for the estimator e. From these, the standard deviation is calculated, which is then interpreted as a standard error. Based on the confidence level, the various intervals are then calculated. Based on the distribution of these estimates, you can calculate the quantiles for a given confidence interval ("PercentileConfidenceInterval"). This will take into account the actual distribution of the underlying estimates. You can also assume this is a normal distribution, and from the CDF of the normal distribution, the number of σ away from the mean is calculated to get the right confidence interval for a certain confidence level ("NormalConfidenceInterval"). If the number of samples is small, a correction can be used based on a Student t distribution ("StudentizedConfidenceInterval").
ResourceFunction["BootstrappedEstimate"] takes the following options:
ConfidenceLevelAutomaticconfidence level to use for confidence intervals
SignificanceLevelAutomaticsignificance level to use for confidence intervals
"Samples"Automaticnumber of samples in each bootstrap
The default ConfidenceLevel is 0.95 (95%, corresponding to a SignificanceLevel of 5%).
The default value for the option "Samples" is the length of the original data.
If both ConfidenceLevel and SignificanceLevel options are given, the value for ConfidenceLevel will be used.

Examples

Basic Examples (1) 

Bootstrap the mean of a randomly created dataset:

In[1]:=
SeedRandom[1234]; r = RandomVariate[NormalDistribution[2.1, 1.25], 100]; ResourceFunction["BootstrappedEstimate"][r, Mean, 1000] // Dataset
Out[3]=

Options (3) 

ConfidenceLevel (1) 

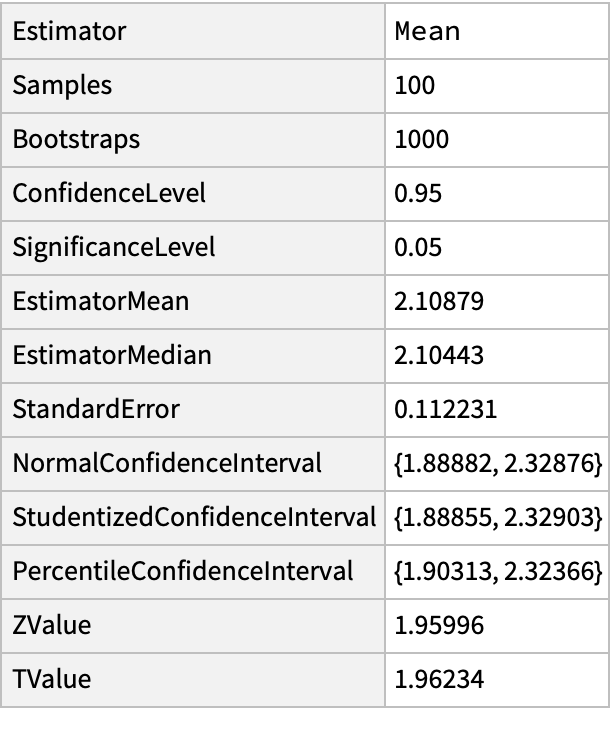Find the Kurtosis and report back the confidence interval corresponding to a 99% confidence level:

In[4]:=
SeedRandom[1234]; r = RandomVariate[NormalDistribution[2.1, 1.25], 100]; ResourceFunction["BootstrappedEstimate"][r, Kurtosis, 1000, ConfidenceLevel -> 0.99] // Dataset
Out[6]=

SignificanceLevel (1) 

Find the Skewness for a 1% significance level:

In[7]:=
SeedRandom[1234]; r = RandomVariate[NormalDistribution[2.1, 1.25], 100]; ResourceFunction["BootstrappedEstimate"][r, Skewness, 1000, SignificanceLevel -> 0.01] // Dataset
Out[9]=

Samples (1) 

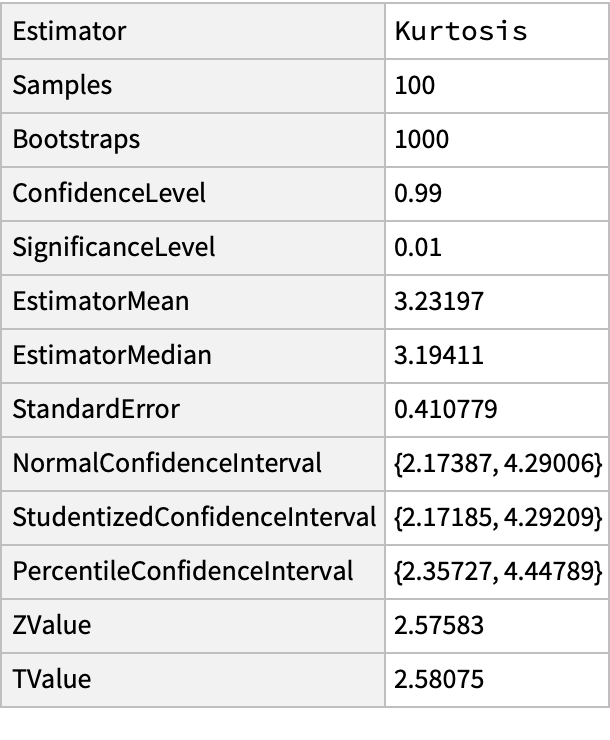Use a higher number of samples for each bootstrap:

In[10]:=
SeedRandom[1234]; r = RandomVariate[NormalDistribution[2.1, 1.25], 100]; ResourceFunction["BootstrappedEstimate"][r, Skewness, 1000, "Samples" -> 1500] // Dataset
Out[12]=

Neat Examples (2) 

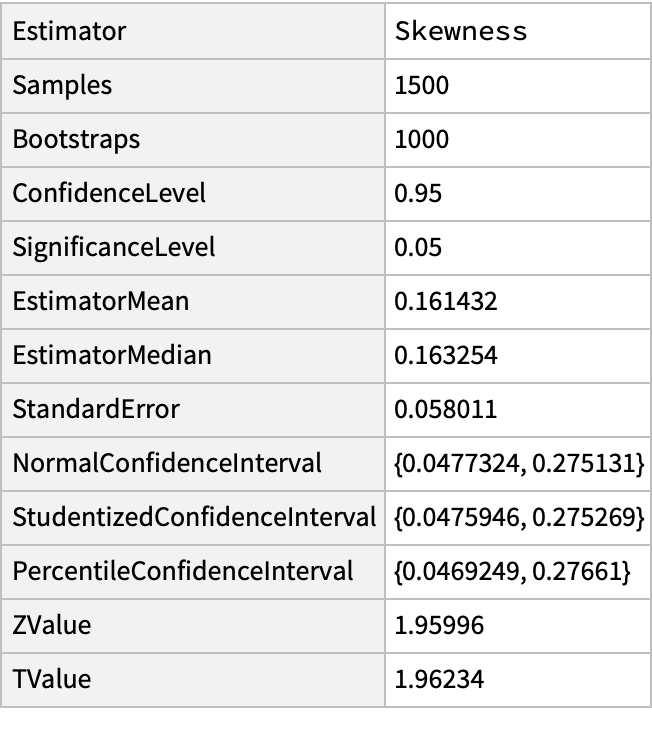Create a random dataset:

In[13]:=
SeedRandom[1234]; x = RandomReal[{-10, 10}, 50]; y = 3 x + 8 + RandomVariate[NormalDistribution[], 50]; data = Transpose[{x, y}]; ListPlot[data]
Out[14]=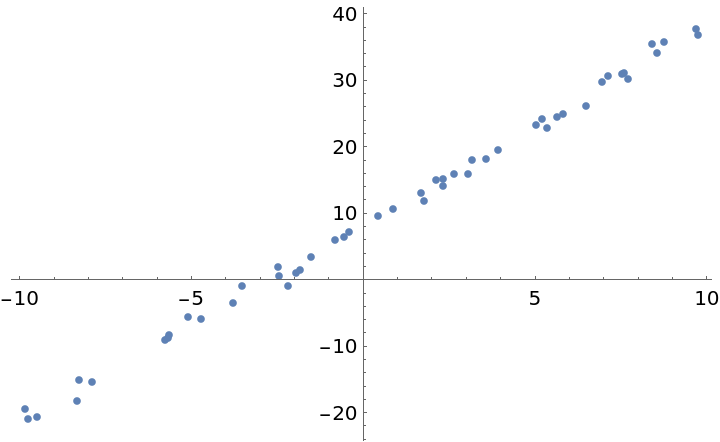

Perform bootstrapping on the slope by doing repeated linear fitting:

In[15]:=
ResourceFunction["BootstrappedEstimate"][data, LinearModelFit[#, {1, \[FormalX]}, \[FormalX]][ "BestFitParameters"][[2]] &, 250] // Dataset
Out[15]=

Publisher

SHuisman

Version History

  • 1.0.0 – 10 August 2021

Source Metadata

  • Citation:
    • Efron, B., "Bootstrap methods: Another look at the jackknife." The Annals of Statistics, vol. 7, no. 1, 1–26, 1979. DOI: 10.1214/aos/1176344552
    • Efron, B., Tibshirani, R.J., An Introduction to the Bootstrap. Boca Raton, FL: CRC Press, 1994.

Related Resources

Author Notes

This only supports estimators with a single scalar output. Could be extended to functions with multiple outputs or multiple functions, but the output is then less clear.

License Information