Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Decompose a matrix into a comprehensive set of smaller matrices
ResourceFunction["BlockSubmatrices"][data,{m,n}] returns a List of associations that decompose data into a complete covering set of submatrices whose elements are partitioned into non-overlapping m×n blocks. |
| "BlockData" | elements of the block submatrix |
| "Offset" | location of the submatrix within initial data |
| "MatrixDimensions" | dimensions of initial data |
| "SubmatrixDimensions" | flat dimensions of the submatrix |
| "Cyclic" | {True,True} | determines cyclic or terminal boundary conditions for row and columns |
| Method | "MinimalCompletion" | specifies how to achieve a complete cover of all possible m×n blocks |
List all 2×2 blocks of a multiplication table:
| In[1]:= |
| Out[1]= |  |
Check the exact covering property against "Atomize" method:
| In[2]:= | ![Apply[SameQ,
Sort[Flatten[#["BlockData"] & /@ ResourceFunction["BlockSubmatrices"][Table[Mod[i j, 5],
{i, 0, 4}, {j, 0, 4}], {2, 2}, Method -> #], 2]
] & /@ {"MinimalCompletion", "Atomize"}]](https://www.wolframcloud.com/obj/resourcesystem/images/74e/74e53f94-3f44-481c-acbc-96bd199403db/1f6c9244f97abe48.png) |
| Out[2]= |
Check completeness and inexactness of the "Lazy" method:
| In[3]:= | ![Function[{filter}, Apply[SameQ,
filter[
Flatten[#["BlockData"] & /@ ResourceFunction["BlockSubmatrices"][Table[Mod[i j, 5],
{i, 0, 4}, {j, 0, 4}], {2, 2}, Method -> #], 2]
] & /@ {"Lazy", "Atomize"}]] /@ {Union, Sort}](https://www.wolframcloud.com/obj/resourcesystem/images/74e/74e53f94-3f44-481c-acbc-96bd199403db/1cb20aa74077c903.png) |
| Out[3]= |
Display a partitioning in graphical form:
| In[4]:= | ![With[{data = Table[Mod[i j, 5], {i, 0, 4}, {j, 0, 4}]},
ReplaceAll[Rule[pl[data], Grid[Partition[
MatrixForm[Map[pl, #["BlockData"], {2}]
] & /@ Flatten[Function[{dims},
Select[ResourceFunction["BlockSubmatrices"][data, {2, 2}],
Dimensions[#["BlockData"]][[{1, 2}]] == dims &]
] /@ {{2, 2}, {2, 1}, {1, 2}, {1, 1}}, 1
][[{1, 2, 5, 3, 4, 6, 7, 8, 9}]], 3],
Frame -> All, Spacings -> {1, 1}, FrameStyle -> LightGray]],
{pl[dat_] :> ArrayPlot[dat, PixelConstrained -> 32,
ColorRules -> MapIndexed[(#2[[1]] - 1) -> Lighter[#1, .5] &,
{Orange, Magenta, Green, Blue, Cyan}], Mesh -> True]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/74e/74e53f94-3f44-481c-acbc-96bd199403db/291087098d977c3c.png) |
| Out[4]= | 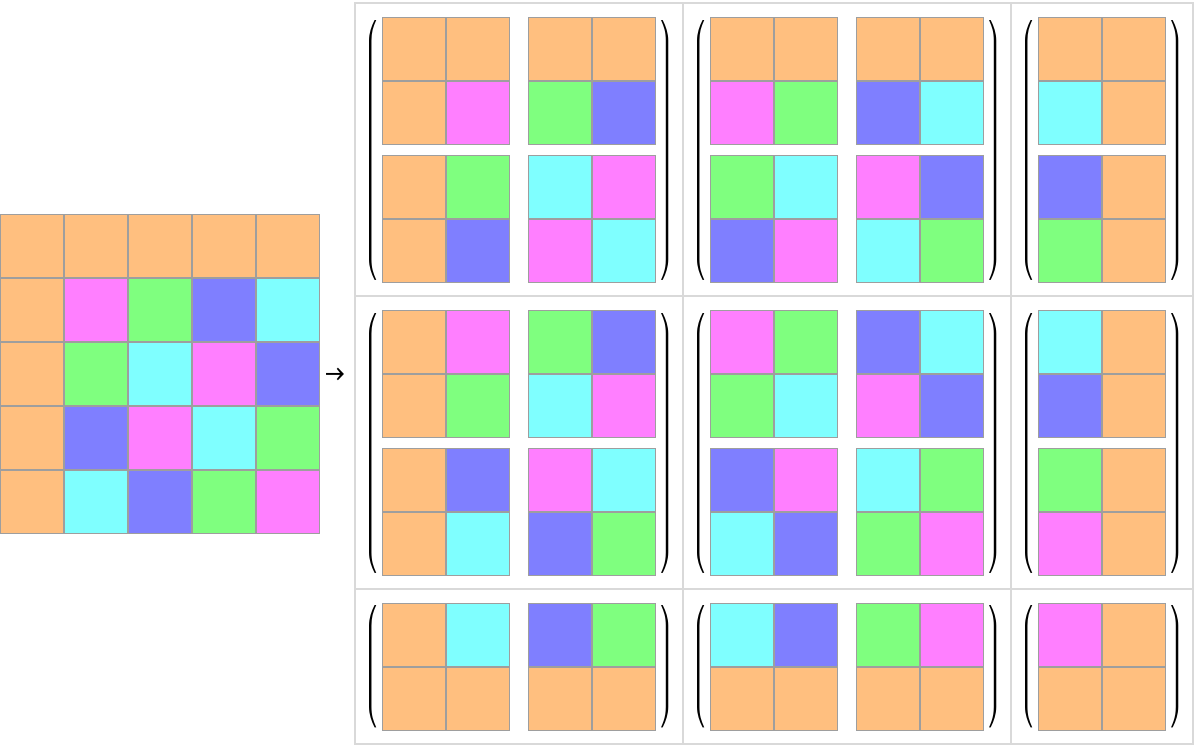 |
Compare with terminal (non-cyclic) boundary conditions:
| In[5]:= | ![With[{data = Table[Mod[i j, 5], {i, 0, 4}, {j, 0, 4}]},
ReplaceAll[Rule[pl[data],
Grid[Partition[ MatrixForm[Map[pl, #["BlockData"], {2}]
] & /@ ResourceFunction["BlockSubmatrices"][data, {2, 2}, "Cyclic" -> {False, False}], 2],
Frame -> All, Spacings -> {1, 1}, FrameStyle -> LightGray]],
{pl[dat_] :> ArrayPlot[dat, PixelConstrained -> 32,
ColorRules -> MapIndexed[(#2[[1]] - 1) -> Lighter[#1, .5] &,
{Orange, Magenta, Green, Blue, Cyan}], Mesh -> True]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/74e/74e53f94-3f44-481c-acbc-96bd199403db/32bb8f06bb895ad2.png) |
| Out[5]= | 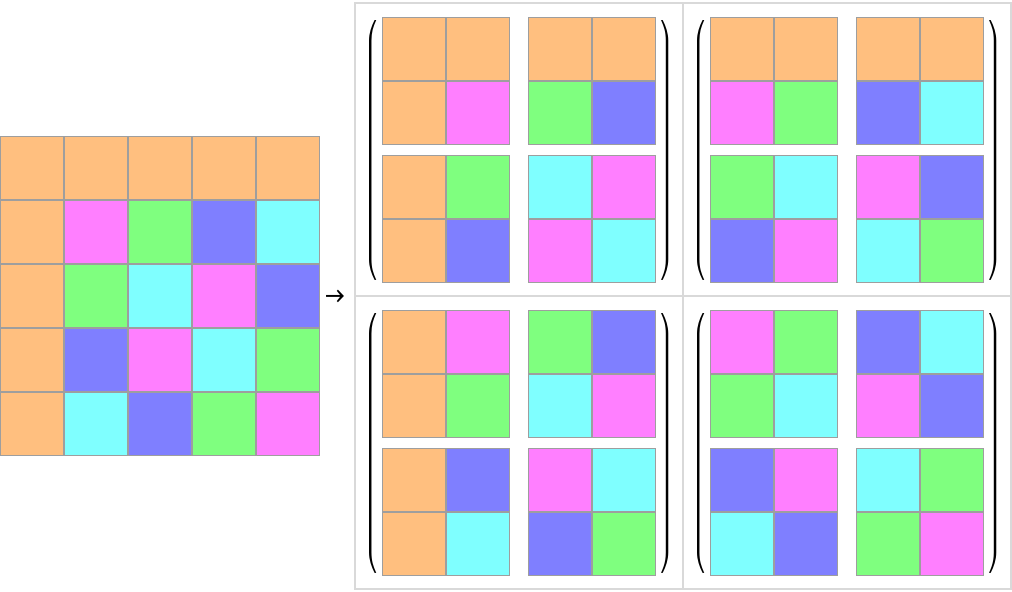 |
It is possible to reconstruct input matrix from any output data set:
| In[6]:= | ![SubmatrixMapping[blockSubmatrix_Association] := With[
{inds = Outer[List, Sequence @@ Mod[
Plus[blockSubmatrix["Offset"],
Range /@ blockSubmatrix["SubmatrixDimensions"]],
blockSubmatrix["MatrixDimensions"], 1], 1]},
MapThread[#1 -> #2 &, {inds,
ArrayFlatten[blockSubmatrix["BlockData"]]}, 2]]](https://www.wolframcloud.com/obj/resourcesystem/images/74e/74e53f94-3f44-481c-acbc-96bd199403db/5b140cc8a9505339.png) |
| In[7]:= | ![RebuildTestSubmatrices[initMat_List, subMatData : {__Association}] := SameQ[
Subtract[initMat, Fold[ReplacePart, Times[0, initMat],
Flatten[SubmatrixMapping[#]] & /@ subMatData]],
Times[0, initMat]]](https://www.wolframcloud.com/obj/resourcesystem/images/74e/74e53f94-3f44-481c-acbc-96bd199403db/4a8e40e860764f16.png) |
| In[8]:= | ![With[{testInput = RandomInteger[5, {2*4*8, 2*4}]},
ArrayPlot[Transpose[testInput],
ColorRules -> (# -> Hue[#/6] & /@ Range[0, 5])
] -> RebuildTestSubmatrices[testInput,
ResourceFunction["BlockSubmatrices"][testInput, RandomInteger[{1, 5}, 2],
"Cyclic" -> RandomChoice[{True, False}, 2],
Method -> RandomChoice[{"MinimalCompletion", "Lazy",
"Overkill", "Atomize"}]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/74e/74e53f94-3f44-481c-acbc-96bd199403db/09bd8060bfd6e876.png) |
| Out[8]= |
This work is licensed under a Creative Commons Attribution 4.0 International License