Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BlockEntropy

Source Notebook

Calculate the joint information entropy of a data matrix

Contributed by: Bradley Klee

ResourceFunction["BlockEntropy"][data]

gives the joint information entropy of data.

ResourceFunction["BlockEntropy"][list,blocksize]

computes the entropy after partitioning list by blocksize.

ResourceFunction["BlockEntropy"][… , macrofun]

groups matrix rows by distinctness of the values macrofun[rowi].

ResourceFunction["BlockEntropy"][… , macrofun,probfun]

allows custom conditional probabilities input through probfun.

ResourceFunction["BlockEntropy"][k,…]

gives the base k joint information entropy.

Details

ResourceFunction["BlockEntropy"] is similar to Entropy in that it also computes values from a sum of the form -∑piLog[pi].
The entropy measurement starts with grouping rows by Total.
Typically, pi is a frequentist probability of obtaining the ith distinct element by randomly sampling the input list.
ResourceFunction["BlockEntropy"] expects a matrix structure, either of the form data={row1,row2,…}, or implicitly as Partition[list,blocksize] ={row1,row2,…}.
Additionally, BlockEntropy allows for coarse-graining of rows to macrostates using the function macrofun (default: Total).
Two rows rowj and rowk, with macrostates mj=macrofun[rowj] and mk=macrofun[rowk], are considered distinct if mj≠mk.
Likewise, two atomistic states dj,x and dk,y are considered distinct if dj,x≠dk,y.
Let 𝒟 be the set of unique atomistic states and ℳ the set of distinct values in the range of macrofun. The joint entropy is then calculated by a double sum, S=-∑ℙ(dj❘mi)ℙ(mi)Log[ℙ(dj❘mi)ℙ(mi)], where indices i and j range over the elements of ℳ and 𝒟 respectively.
The frequentist probability ℙ(mi) , mi∈ℳ equals the count of rows satisfying mi=macrofun[rowj], divided by the total number of rows.
The conditional probability ℙ(dj❘mi), mi∈ℳ, dj∈𝒟 is not necessarily frequentist, but is often assumed or constructed to be so.
The optional function probfun takes mi∈ℳ as the first argument and blocksize as the second argument. It should return an Association or List of conditional probabilities ℙ(dj❘mi).
When probfun is not set, either "Micro" or "Macro" conditional probabilities can be specified by setting the "Statistics" option.
The default "Micro" statistics obtains 𝒟 by taking a Union over row elements. The conditional probabilities are then calculated as ℙ(dj❘mi)=∑ℙ(dj❘rowk)ℙ(rowk)=∑ℙ(dj❘rowk) /N, where the sum includes every possible rowk written over elements 𝒟 and satisfying mi=macrofun[rowk]. The factor 1/ℙ(rowk)=N equals the Count of such rows, all assumed equiprobable.
Traditional "Macro" statistics require that 𝒟 contains all possible rows of the correct length whose elements are drawn from the complete set of row elements using Tuples. The conditional probabilities are then calculated as ℙ(dj❘mi)=0 if mi≠macrofun[dj] or if mi=macrofun[dj] as ℙ(dj❘mi)=1 /N, with N equal to the count of atomistic row states dk satisfying mi=macrofun[dk].

Examples

Basic Examples (4) 

Calculate the BlockEntropy of a binary matrix:

In[1]:=
ResourceFunction["BlockEntropy"][{{0, 1}, {0, 1}, {0, 1}}]
Out[1]=

The BlockEntropy value does not change by permuting in block:

In[2]:=
ResourceFunction["BlockEntropy"][{{0, 1}, {0, 1}, {1, 0}}]
Out[2]=

Calculate the ternary BlockEntropy of a binary list:

In[3]:=
ResourceFunction["BlockEntropy"][{0, 0, 1, 0, 1, 1, 1, 1, 1}, 3]
Out[3]=

Calculate the same value from a matrix input:

In[4]:=
ResourceFunction["BlockEntropy"][{{0, 0, 1}, {0, 1, 1}, {1, 1, 1}}]
Out[4]=

The BlockEntropy value does not change by permuting blocks:

In[5]:=
ResourceFunction["BlockEntropy"][{{0, 1, 1}, {1, 1, 1}, {0, 0, 1}}]
Out[5]=

Calculate the ternary entropy of a binary list assuming isentropic macrostates:

In[6]:=
ResourceFunction["BlockEntropy"][{0, 1, 1, 1, 1, 1, 0, 0, 1}, 3, Entropy@# &]
Out[6]=

Changing the aggregation function can change the BlockEntropy value:

In[7]:=
ResourceFunction["BlockEntropy"][{0, 1, 1, 1, 1, 1, 0, 0, 1}, 3]
Out[7]=

Two different aggregation functions can have the same asymptotics:

In[8]:=
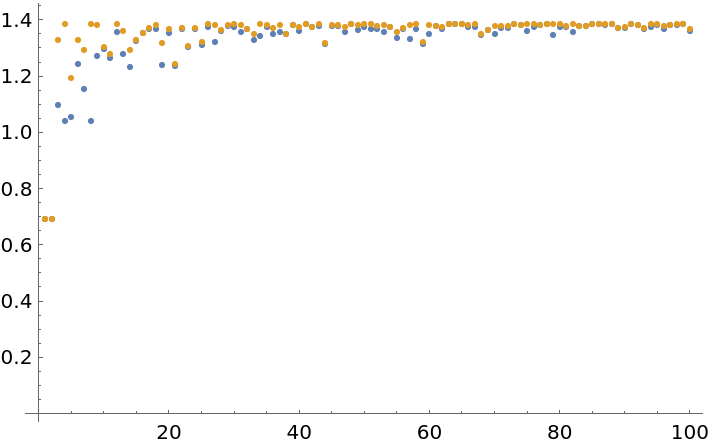
ListPlot[Transpose[Abs[List[ ResourceFunction["BlockEntropy"][SeedRandom[Floor[10^6 Pi^#]]; RandomInteger[1, {#, 2}], Total], ResourceFunction["BlockEntropy"][SeedRandom[Floor[10^6 Pi^#]]; RandomInteger[1, {#, 2}], Entropy] ]] & /@ Range[100]], PlotRange -> All]
Out[8]=

Scope (2) 

BlockEntropy accepts lists of arbitrary arity:

In[9]:=
ResourceFunction["BlockEntropy"][{x, y, a, x, a, b, c, x}, 4]
Out[9]=

Treat each macrostate as equiprobable:

In[10]:=
ResourceFunction["BlockEntropy"][CompoundExpression[ SeedRandom[144234], RandomInteger[5, 100] ], 5, Total, Function[{any}, {1}]]
Out[10]=

Compare with more simple means:

In[11]:=
With[{rand = CompoundExpression[ SeedRandom[144234], RandomInteger[5, 100]]}, Equal[ResourceFunction["BlockEntropy"][rand, 5, Total, Function[{any}, {1}]], Entropy[Total /@ Partition[rand, 5]]]]
Out[11]=

Options (4) 

BlockEntropy provides different built-in statistics:

In[12]:=
Map[# -> ResourceFunction["BlockEntropy"][SeedRandom[324313]; RandomInteger[2, 12], 3, "Statistics" -> #] &, {"Micro", "Macro"}] // Column
Out[12]=

Setting Statistics to "Macro" can make normal Entropy easier to predict:

In[13]:=
N[Subtract[ResourceFunction["BlockEntropy"][ RandomInteger[2, 10^6 + 2], 3, "Statistics" -> "Macro"], Log[3^3]]]
Out[13]=

Alternative statistics can sometimes have opposite behaviors:

In[14]:=
ListLinePlot[Outer[N@ResourceFunction["BlockEntropy"][ Table[PadLeft[{1}, #2], 10], "Statistics" -> #1] &, {"Micro", "Macro"}, Range[2, 10], 1]]
Out[14]=

Compare with the theoretical result:

In[15]:=
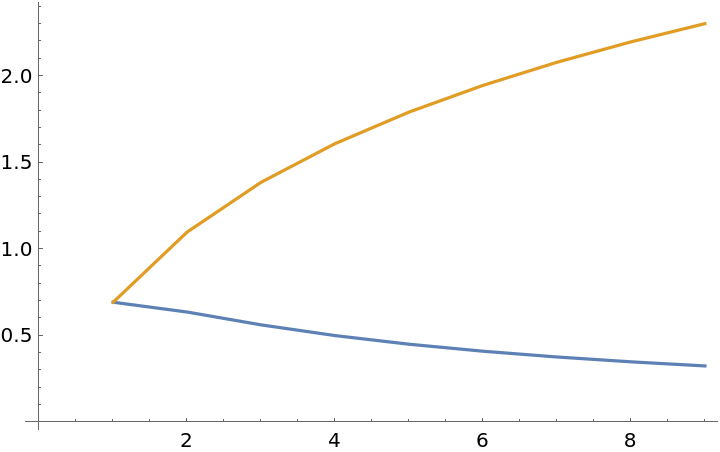
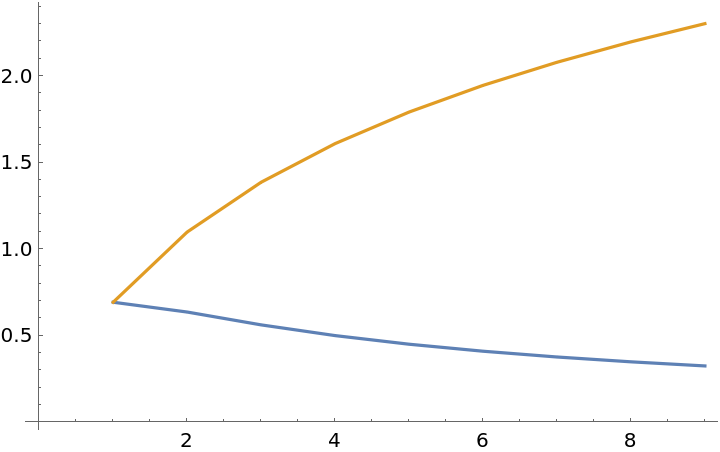
ListLinePlot[Transpose[{ -1/# Log[1/#] - (# - 1)/# Log[(# - 1)/#], -Log[1/#]} & /@ Range[2, 10]]]
Out[15]=

Applications (1) 

Measure the entropy time series of a cellular automaton:

In[16]:=
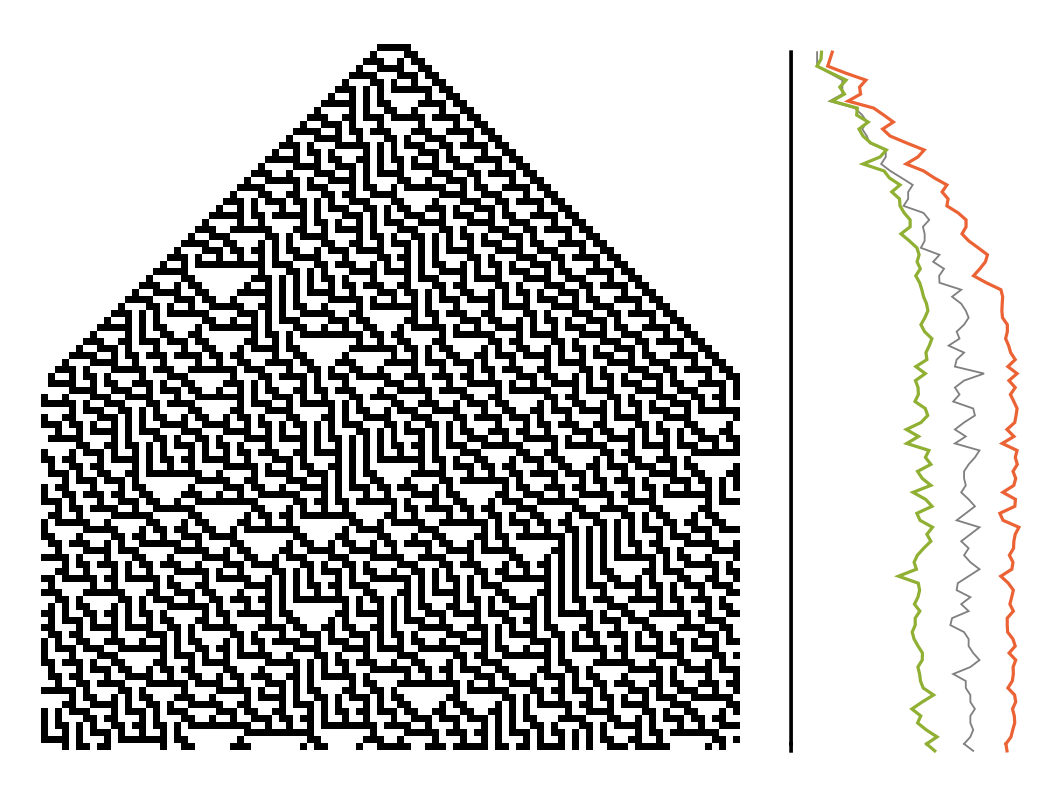
ImageRotate[GraphicsColumn[{ListLinePlot[{ 0 & /@ #, Entropy[Partition[#, 5]] & /@ #, ResourceFunction["BlockEntropy"][#, 5, "Statistics" -> "Micro"] & /@ #, ResourceFunction["BlockEntropy"][#, 5, "Statistics" -> "Macro"] & /@ # }, PlotStyle -> { Directive[Thickness[0.005], Black], Directive[Thickness[0.0025], Gray], Automatic, Automatic}, Ticks -> False, Axes -> False, ImageSize -> {400, Automatic}, AspectRatio -> 1/3], ArrayPlot[ Transpose[#], Frame -> None, ImageSize -> {400, Automatic}] } &@CellularAutomaton[30, CenterArray[{1, 1, 1, 1, 1}, 100], 100]], -Pi/2]
Out[16]=

Properties and Relations (3) 

The Entropy of a list equals the BlockEntropy of a column matrix with the same elements:

In[17]:=
Equal[ResourceFunction["BlockEntropy"][List /@ #], Entropy[#]] &@ RandomInteger[10, 100]
Out[17]=

BlockEntropy can return the same value as a naive combination of Partition and Entropy:

In[18]:=
With[{rand = RandomInteger[2, 25]}, Equal[Entropy[Partition[rand, 5]], ResourceFunction["BlockEntropy"][rand, 5, Identity, "Statistics" -> "Macro"]]]
Out[18]=

The BlockEntropy of a constant density binary matrix equals the Entropy of any row:

In[19]:=
Equal[ResourceFunction["BlockEntropy"][RandomSample /@ Table[#, 5]], Entropy[#]] &@RandomInteger[1, 10]
Out[19]=

But this relation does not hold in general:

In[20]:=
SeedRandom[1234]; Equal[ResourceFunction["BlockEntropy"][RandomSample /@ Table[#, 5]], Entropy[#]] &@RandomInteger[2, 5]
Out[5]=

Possible Issues (3) 

If an incommensurate block length is chosen, some values will be dropped:

In[21]:=
ResourceFunction["BlockEntropy"][{12, 3, 4, 5, 6, 6, 5, 7}, 3]
Out[21]=

The message refers to the underlying behavior of Partition:

In[22]:=
Partition[{12, 3, 4, 5, 6, 6, 5, 7}, 3]
Out[22]=

Thus the same BlockEntropy value may be computed as:

In[23]:=
ResourceFunction["BlockEntropy"][{{12, 3, 4}, {5, 6, 6}}]
Out[23]=

Neat Examples (2) 

Classify all length 4 ternary lists according to their binary BlockEntropy:

In[24]:=
Grid[KeyValueMap[{#1, Row[#2, Spacer[1]]} &, Map[ArrayPlot[Partition[#, 2], Mesh -> True, ImageSize -> 30, ColorRules -> {a -> Red, b -> Green, c -> Blue}] &, KeySort[ GroupBy[Tuples[{a, b, c}, 4], ResourceFunction["BlockEntropy"][#, 2, Entropy] &], NumericalOrder], {2}]], Frame -> All, FrameStyle -> LightGray, Alignment -> Left, Spacings -> {3, 1}]
Out[24]=

Test the randomness of the binary digits of π:

In[25]:=
N[Subtract[ ResourceFunction["BlockEntropy"][ First[RealDigits[Pi, 2, #*100000]], #, Total, "Statistics" -> "Macro"], Log[2^#]]] & /@ Range[2, 5]
Out[25]=

Publisher

Brad Klee

Version History

  • 1.0.0 – 28 September 2022

Related Resources

License Information