Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evolve a block cellular automaton
ResourceFunction["BlockCellularAutomaton"][rule,init,t,phase] generates a list representing the evolution of the block cellular automaton with the specified rule from initial condition init for t steps, starting in the specified phase. | |
ResourceFunction["BlockCellularAutomaton"][rule,init] gives the result of evolving init for one step, with phase 1. | |
ResourceFunction["BlockCellularAutomaton"][rule,phase] is an operator form of ResourceFunction["BlockCellularAutomaton"] that represents one step of evolution. |
Run a block cellular automaton for 20 steps:
| In[1]:= |
|
| Out[1]= |

|
Evolve a block cellular automaton for three steps:
| In[2]:= |
|
| Out[2]= |
|
Give the result of one step of evolution:
| In[3]:= |
|
| Out[3]= |
|
The operator form equivalent:
| In[4]:= |
|
| Out[4]= |
|
Use an "algebraic" replacement rule:
| In[5]:= |
|
| Out[5]= |

|
A block cellular automaton from A New Kind of Science:
| In[6]:= |
![ArrayPlot[
ResourceFunction["BlockCellularAutomaton", ResourceVersion->"1.0.0"][{{2, 2} -> {1, 1}, {1, 1} -> {2, 2}, {1, 2} -> {1, 2}, {2, 1} -> {2, 1}, {2, 0} -> {0, 2}, {1, 0} -> {1, 0}, {0, 2} -> {2, 0}, {0, 1} -> {0, 1}, {0, 0} -> {0, 0}}, CenterArray[Table[2, 38], 100], 300, 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/67f/67fa78cf-815d-40ba-85cc-918b434275ac/1-0-0/0c1cd350d7dbbade.png)
|
| Out[6]= |
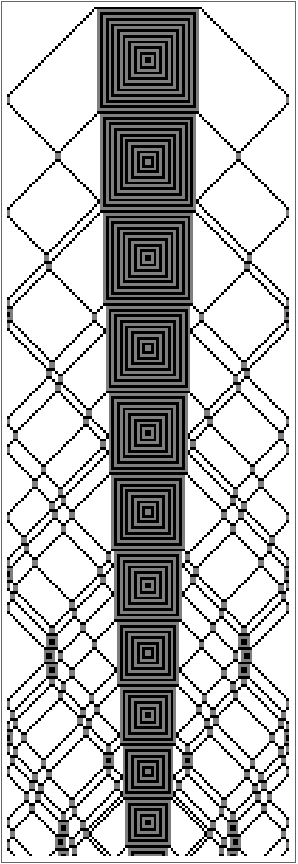
|
Examples of block cellular automata with more general replacement rules:
| In[7]:= |
![ArrayPlot[
ResourceFunction["BlockCellularAutomaton", ResourceVersion->"1.0.0"][# -> CellularAutomaton[110][#] & /@ Tuples[{1, 0}, 3], CenterArray[{1}, 200], 100, 2]]](https://www.wolframcloud.com/obj/resourcesystem/images/67f/67fa78cf-815d-40ba-85cc-918b434275ac/1-0-0/0d4769f2cd60b0c4.png)
|
| Out[7]= |
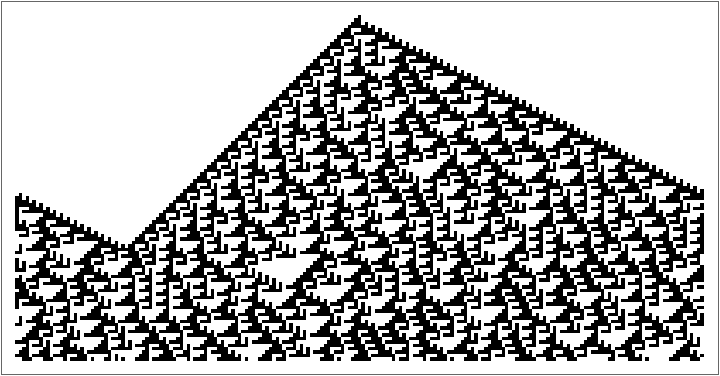
|
| In[8]:= |
|
| Out[8]= |

|
This work is licensed under a Creative Commons Attribution 4.0 International License