Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Apply a Boolean function to corresponding bits in integers
ResourceFunction["BitBooleanFunction"][k][x,y] computes the kth bitwise Boolean function of the integers x and y. | |
ResourceFunction["BitBooleanFunction"][k,n][x1,…,xn] computes the kth n-input bitwise Boolean function of the integers xi. |
Compute the sixth bitwise Boolean function:
| In[1]:= |
|
| Out[1]= |
|
This corresponds to computing a bitwise XOR:
| In[2]:= |
|
| Out[2]= |
|
Compute the 150th bitwise Boolean function with three inputs:
| In[3]:= |
|
| Out[3]= |
|
Plot of a Boolean function:
| In[4]:= |
|
| Out[4]= |
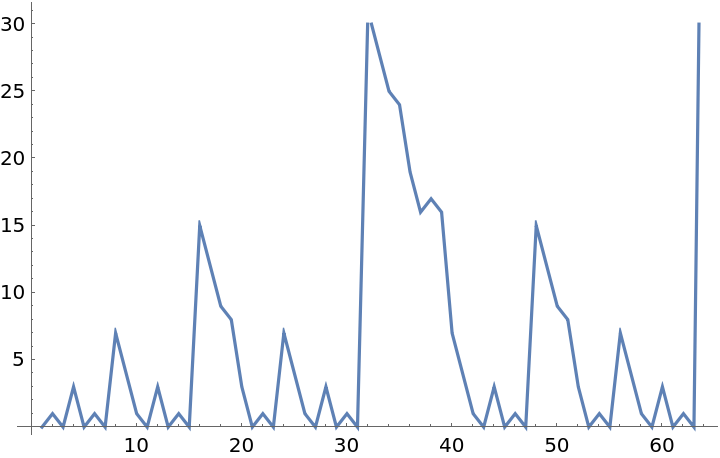
|
A 2D plot of Boolean function versus Mod[i, j]:
| In[5]:= |
|
| Out[5]= |
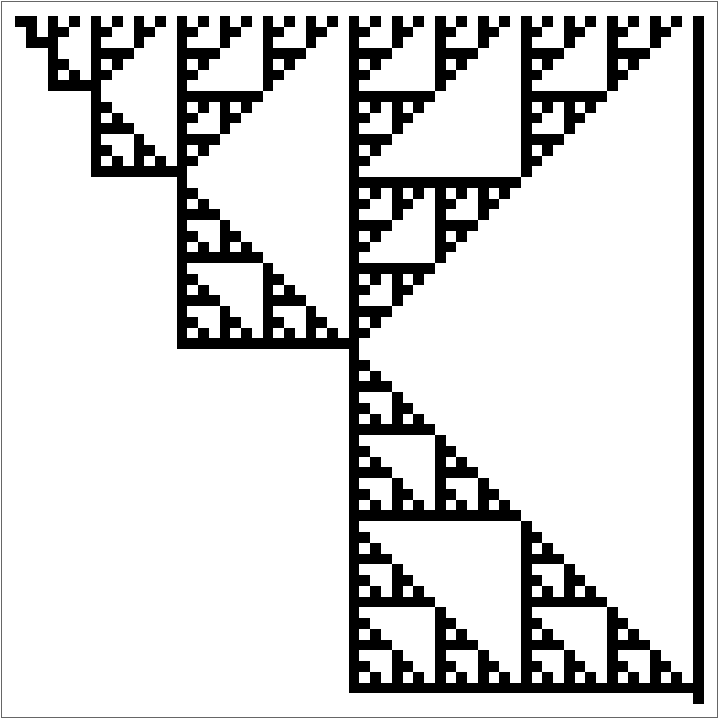
|
A 3D plot of a Boolean function:
| In[6]:= |
|
| Out[6]= |

|
Recover the index of a bitwise Boolean function:
| In[7]:= |
|
| Out[7]= |
|
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License