Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Determine the root of an equation using the bisection method
ResourceFunction["BisectionMethodFindRoot"][f,{x,xa,xb},tol,n] searches for a numerical root of f between the points xa and xb using tol digits and up to n steps. | |
ResourceFunction["BisectionMethodFindRoot"][lhs⩵rhs,{x,xa,xb},tol,n] searches for a numerical solution to the equation lhs==rhs. | |
ResourceFunction["BisectionMethodFindRoot"][f,{x,xa,xb},tol,n,property] returns a property of the search for the root of f. |
| "Solution" | return the root of f |
| "Steps" | return a table of steps taken to reach the root |
Find the root of an expression using the bisection method:
| In[1]:= |
| Out[1]= |
Determine the steps to find the root of an equation:
| In[2]:= |
| Out[2]= | 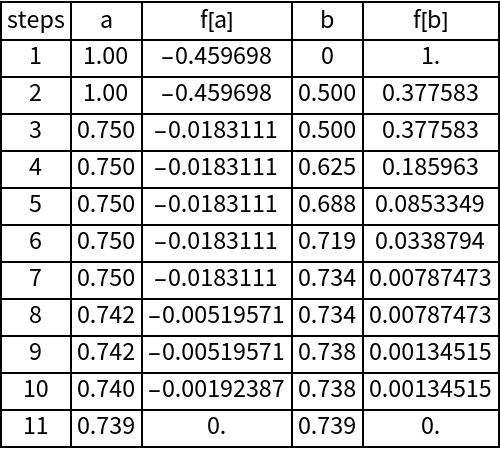 |
Get the property association of a bisection search:
| In[3]:= |
| Out[3]= | 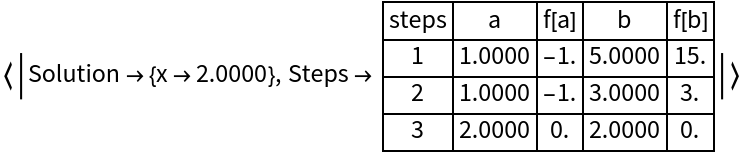 |
This work is licensed under a Creative Commons Attribution 4.0 International License