Basic Examples (4) 

Compute Fibonacci numbers:

In[1]:=

Out[1]=

Generalize to real-valued inputs:

In[2]:=

Out[2]=

In[3]:=

Out[3]=

Use symbolic inputs:

In[4]:=

Out[4]=

Compare to the formula used by Fibonacci:

In[5]:=

Out[5]=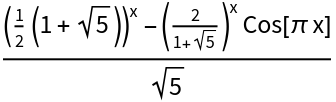

Plot the real and imaginary components:

In[6]:=

Out[6]=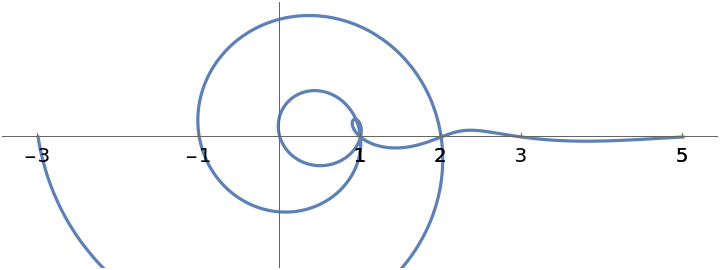

Scope (4) 

Evaluate numerically:

In[7]:=

Out[7]=

In[8]:=

Out[8]=

Evaluate to high precision:

In[9]:=

Out[9]=

Compare the real component to Fibonacci:

In[10]:=

Out[10]=

The precision of the output tracks the precision of the input:

In[11]:=

Out[11]=

Complex number inputs:

In[12]:=

Out[12]=

In[13]:=

Out[13]=

Properties and Relations (5) 

The curve intersects the real axis at the Fibonacci numbers:

In[14]:=

Out[14]=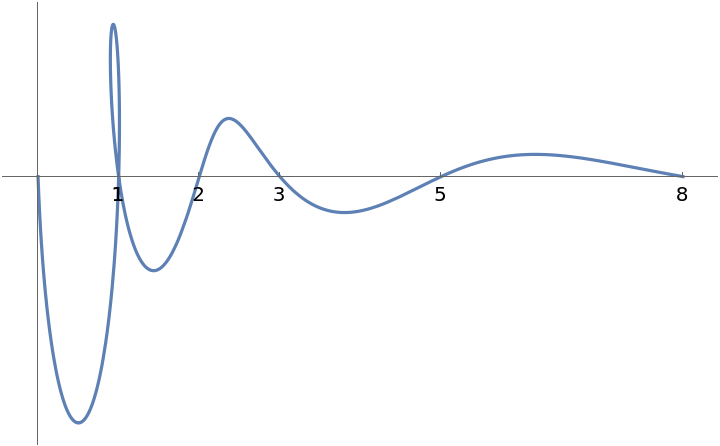

Negative inputs produce a spiral in order to alternate between positive and negative values:

In[15]:=

Out[15]=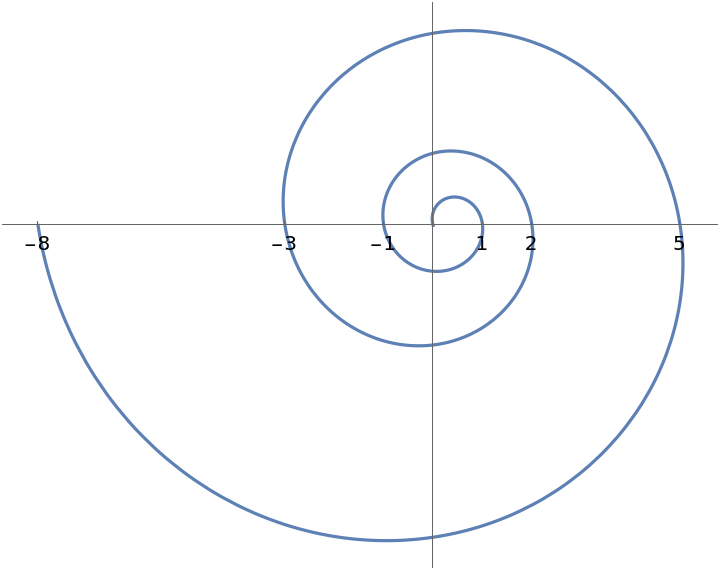

Verify with Fibonacci:

In[16]:=

Out[16]=

For real n, Re[BinetFibonacci[n]] is equivalent to Fibonacci[n]:

In[17]:=

Out[17]=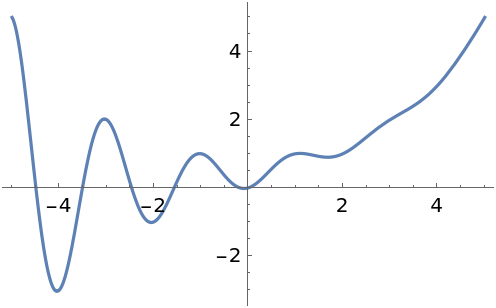

In[18]:=

Out[18]=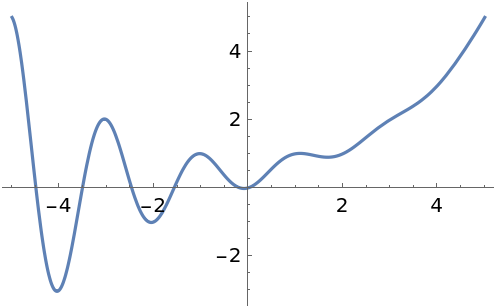

BinetFibonacci automatically threads over lists:

In[19]:=

Out[19]=

For large lists, it is more efficient to apply BinetFibonacci directly to the List rather than mapping it:

In[20]:=

In[21]:=

Out[21]=

In[22]:=

Out[22]=

Possible Issues (2) 

The numerical error can become significant for larger values due to differing formulas:

In[23]:=

Out[23]=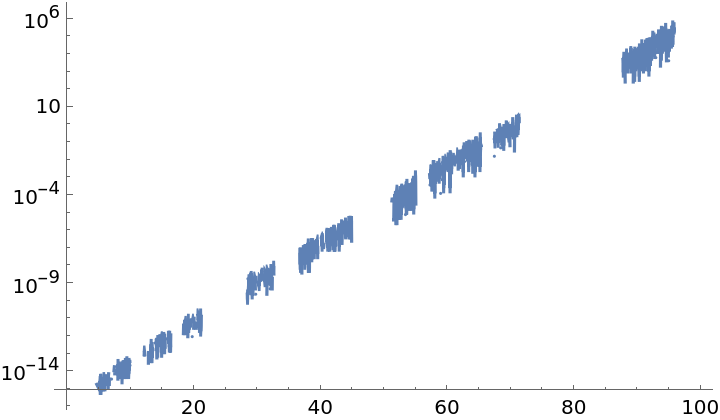

The resource function InverseFibonacci does not accept the complex values produced by BinetFibonacci:

In[24]:=

Out[24]=

Extract the real component first using Re:

In[25]:=

Out[25]=