Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BinetCauchyIdentity

Source Notebook

Verifies the Binet–Cauchy algebraic identity in a given dimension

Contributed by: Eric W. Weisstein

ResourceFunction["BinetCauchyIdentity"][n]

verifies the Binet–Cauchy algebraic identity.

Details and Options

The Binet–Cauchy algebraic identity:

Examples

Basic Examples (5) 

For n=2:

In[1]:=
ResourceFunction["BinetCauchyIdentity"][2]
Out[1]=

For n=3:

In[2]:=
ResourceFunction["BinetCauchyIdentity"][3]
Out[2]=

The previous output is equivalent to the vector identity:

In[3]:=
Array[a, 3] . Array[c, 3] Array[b, 3] . Array[d, 3] - Array[a, 3] . Array[d, 3] Array[b, 3] . Array[c, 3] == Cross[Array[a, 3], Array[b, 3]] . Cross[Array[c, 3], Array[d, 3]] /. a_[k_] :> Subscript[a, k]
Out[3]=

Verify the identity up to n=10:

In[4]:=
Expand //@ Table[ResourceFunction["BinetCauchyIdentity"][n], {n, 10}]
Out[4]=

A subscripted version:

In[5]:=
Table[ResourceFunction["BinetCauchyIdentity"][n] /. a_[k_] :> Subscript[a, k], {n, 2, 3}]
Out[5]=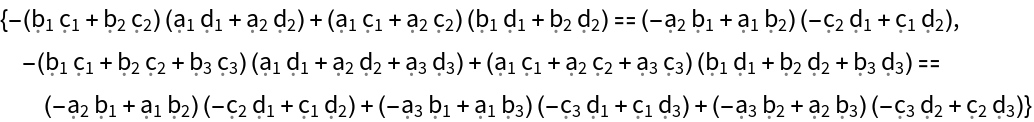

Degenerates to Lagrange's identity:

In[6]:=
Table[ResourceFunction["BinetCauchyIdentity"][ n] /. {\[FormalC] -> \[FormalA], \[FormalD] -> \[FormalB]} /. a_[k_] :> Subscript[a, k], {n, 2, 3}]
Out[6]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 06 March 2019

License Information