Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BilliardPolygon

Source Notebook

Show the trajectory of a ball bouncing in a regular n-sided polygon

Contributed by: Robert Dickau, Eric W. Weisstein

ResourceFunction["BilliardPolygon"][sides,pos,θ,t]

gives the trajectory of a ball in a regular n-sided polygon starting from position pos with an angle θ for t steps.

Details and Options

Mathematical billiards consists of a ball bouncing with no friction against the sides of a plane or higher-dimensional object, in this case, a regular polygon. The trajectories show interesting behavior related to dynamical systems theory.

Examples

Basic Examples (4) 

Start with a triangle with a hundred steps:

In[1]:=
ResourceFunction["BilliardPolygon"][3, {0.155`, 0.27`}, 0.508`, 100]
Out[1]=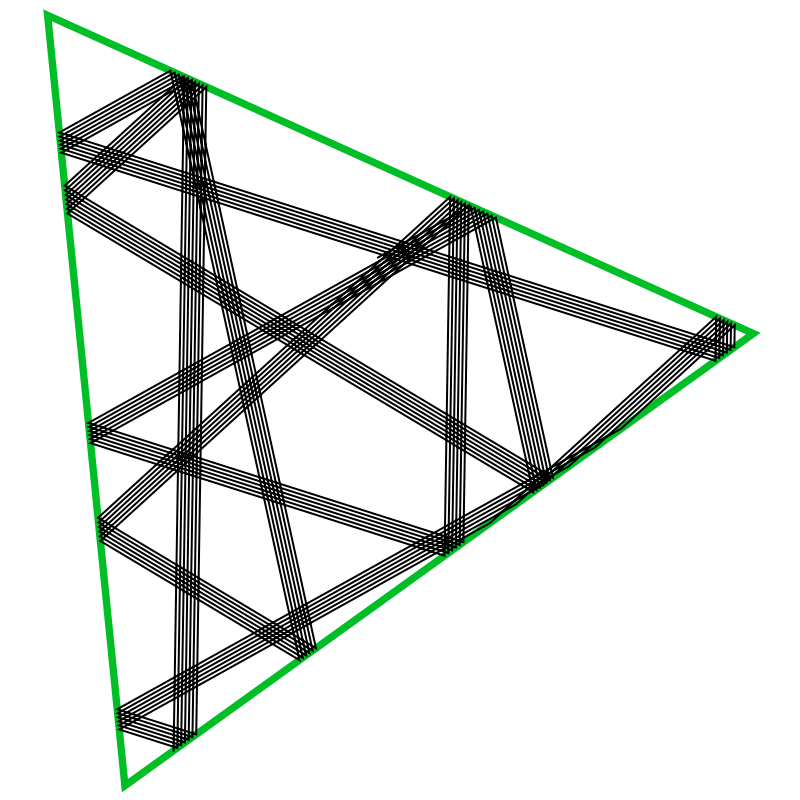

15 steps in the evolution for several geometries:

In[2]:=
GraphicsGrid[{Table[ ResourceFunction["BilliardPolygon"][n, {.01, .1}, \[Pi]/12, 15], {n, 3, 5}]}, ImageSize -> 600]
Out[2]=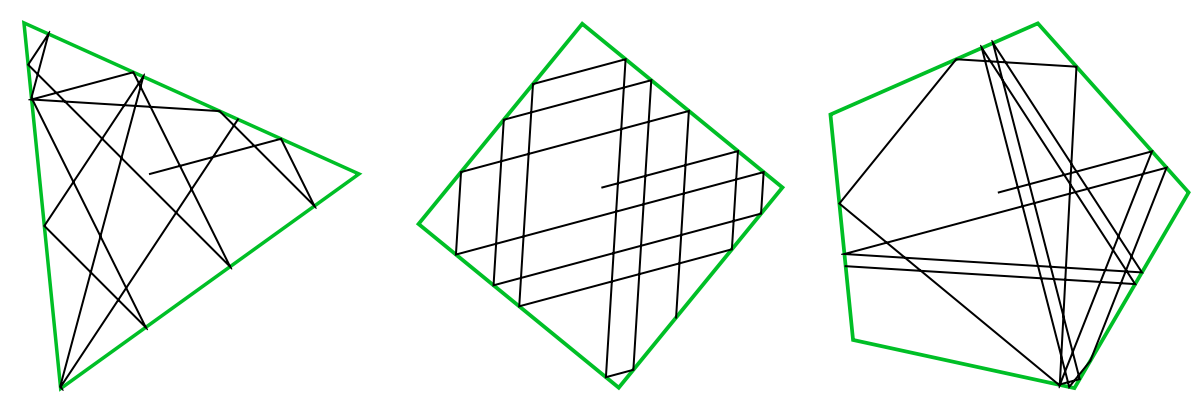

Increment gradually the initial position in y-axis:

In[3]:=
Animate[ResourceFunction["BilliardPolygon"][3, {.1, dx}, \[Pi]/12, 50], {dx, 0, .5, .01}]
Out[3]=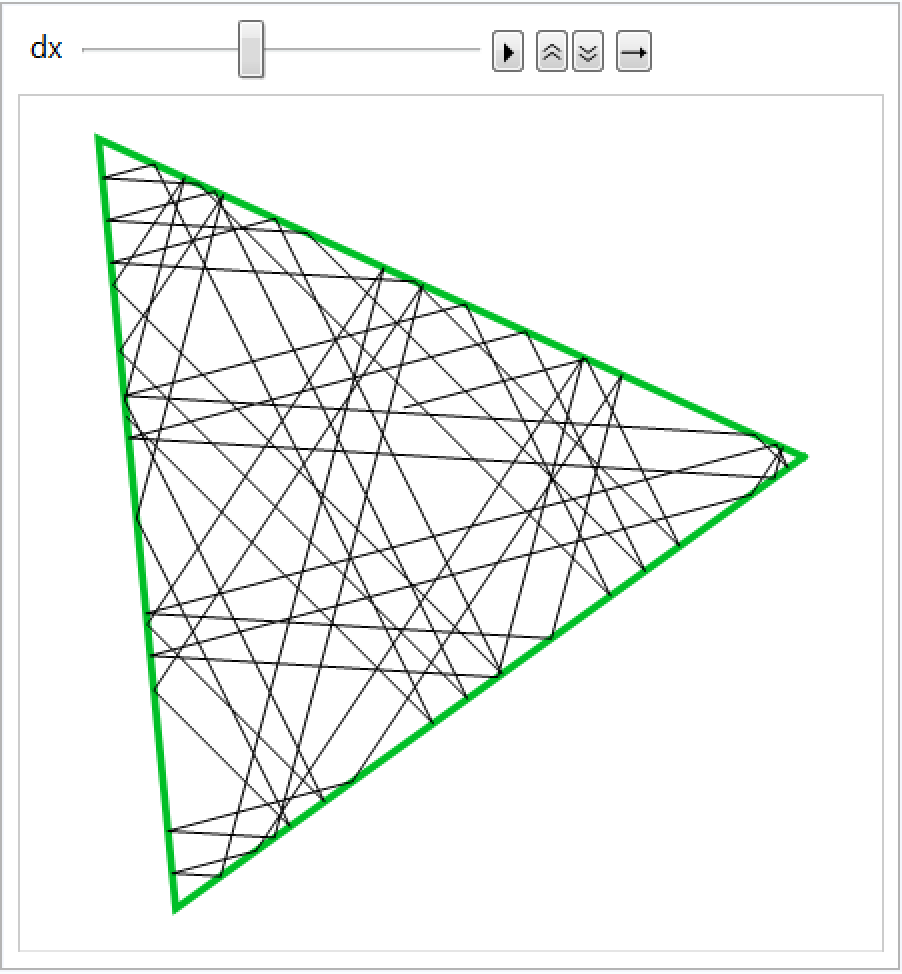

A higher number of steps:

In[4]:=
ResourceFunction["BilliardPolygon"][5, {0.454, 0.096`}, 1.246`, 263]
Out[4]=

Requirements

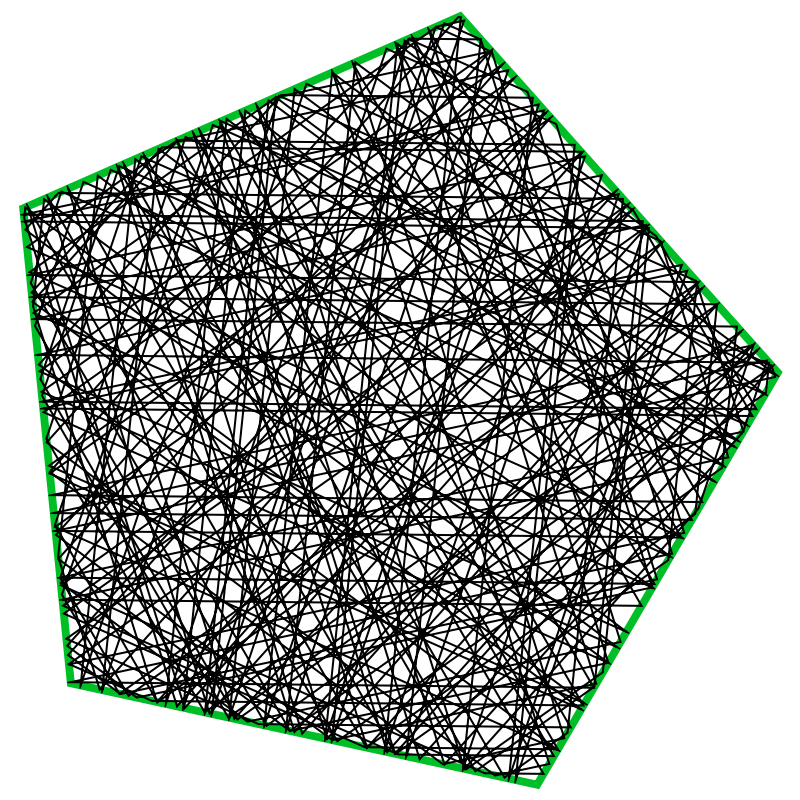Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 01 March 2019

License Information