Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Modify Graph to include extraverted double edges
ResourceFunction["BidirectedGraph"][g] returns graph g, styled as a bidirectional graph, by default collapsing 2-cycles into extraverted edges. | |
ResourceFunction["BidirectedGraph"][{e1,e2,…}] returns the graph with edges ej, styled as a bidirectional graph, by default collapsing 2-cycles into extraverted edges. |
Force two-cycles from DirectedGraph to overlap:
| In[1]:= |
| Out[1]= | 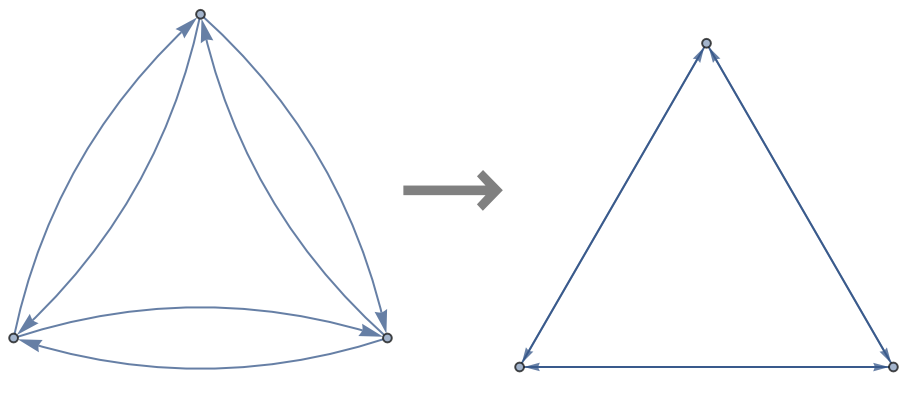 |
Do not collapse edges:
| In[2]:= | ![Row[{#, Style["\[LongRightArrow]", Gray, Bold, 40], ResourceFunction["BidirectedGraph"][#, Options[#], "Filter" -> False]}] &@DirectedGraph[
UndirectedEdge @@ # & /@ Partition[Range[3], 2, 1, 1], ImageSize -> 200]](https://www.wolframcloud.com/obj/resourcesystem/images/824/82403039-c8f3-4599-97e3-86afe3939864/7d10c69032c8c604.png) |
| Out[2]= |  |
Instead of converting graphs, specify edges directly:
| In[3]:= | ![With[{edges = DirectedEdge @@ # & /@ Tuples[Range[4], 2]},
Row[{Graph[edges, ImageSize -> 200],
Style["\[LongRightArrow]", Gray, Bold, 40],
ResourceFunction["BidirectedGraph"][edges, ImageSize -> 200]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/824/82403039-c8f3-4599-97e3-86afe3939864/6a7f9500c04d479e.png) |
| Out[3]= | 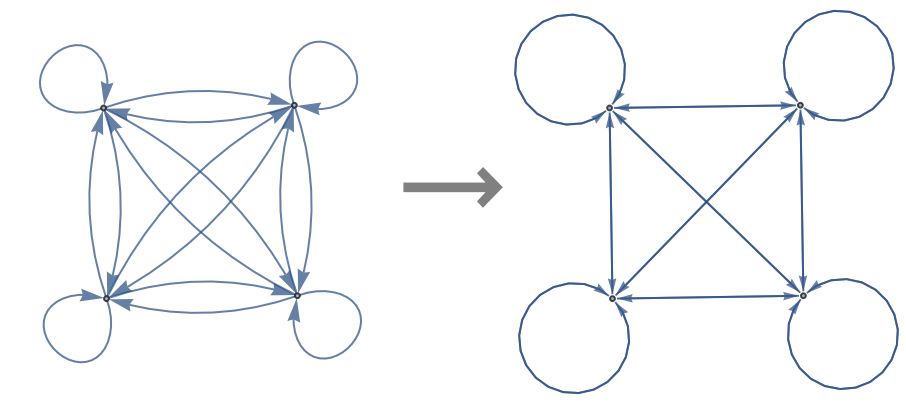 |
BidirectedGraph supports four different edge specifications:
| In[4]:= | ![With[{edges = {
UndirectedEdge[1, 4],
DirectedEdge[1, 2],
DirectedEdge[2, 1],
LeftRightArrow[2, 3],
3 -> 4,
DirectedEdge[4, 3]}},
ResourceFunction["BidirectedGraph"][edges, "Filter" -> #] & /@ {False, True}
]](https://www.wolframcloud.com/obj/resourcesystem/images/824/82403039-c8f3-4599-97e3-86afe3939864/223fd16675d87d3a.png) |
| Out[4]= | 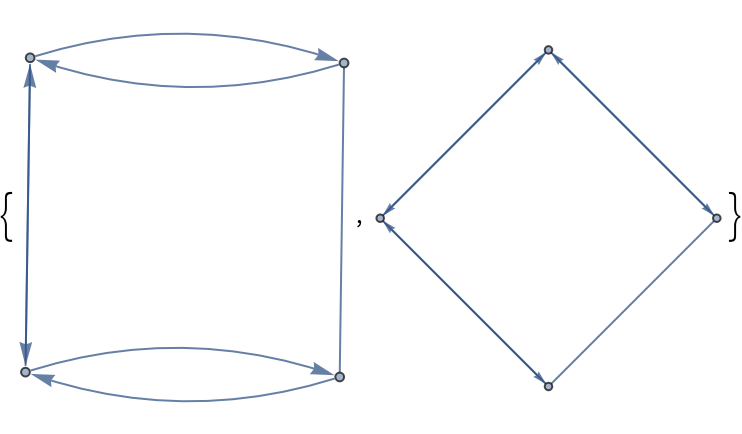 |
Due to hacking of Graph, edge colorings may work out incorrectly:
| In[5]:= | ![ResourceFunction["BidirectedGraph"][{
UndirectedEdge[1, 4],
DirectedEdge[1, 2],
DirectedEdge[2, 1],
LeftRightArrow[2, 3],
3 -> 4,
DirectedEdge[4, 3]},
"Filter" -> False,
{VertexStyle -> Red,
EdgeStyle -> {
LeftRightArrow[_, _] -> Red,
DirectedEdge[_, _] -> Green}}]](https://www.wolframcloud.com/obj/resourcesystem/images/824/82403039-c8f3-4599-97e3-86afe3939864/09991740376fb269.png) |
| Out[5]= | 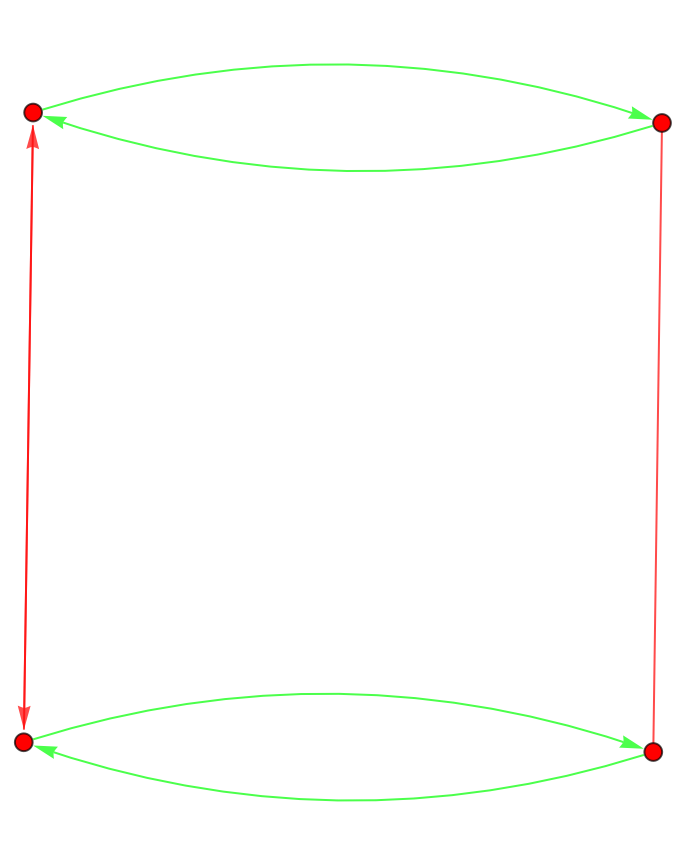 |
However, with more care, it is possible to get correct colorings:
| In[6]:= | ![With[{edges = {UndirectedEdge[1, 4],
DirectedEdge[1, 2],
DirectedEdge[2, 1],
LeftRightArrow[2, 3],
3 -> 4,
DirectedEdge[4, 3]}},
ResourceFunction["BidirectedGraph"][edges, "Filter" -> False, EdgeStyle -> MapThread[
Alternatives @@ (Cases[edges, #1[_, _]]) -> #2 &,
{{DirectedEdge, LeftRightArrow, UndirectedEdge}, {Red, Green, Blue}}
]]]](https://www.wolframcloud.com/obj/resourcesystem/images/824/82403039-c8f3-4599-97e3-86afe3939864/43269329bbbe7f59.png) |
| Out[6]= | 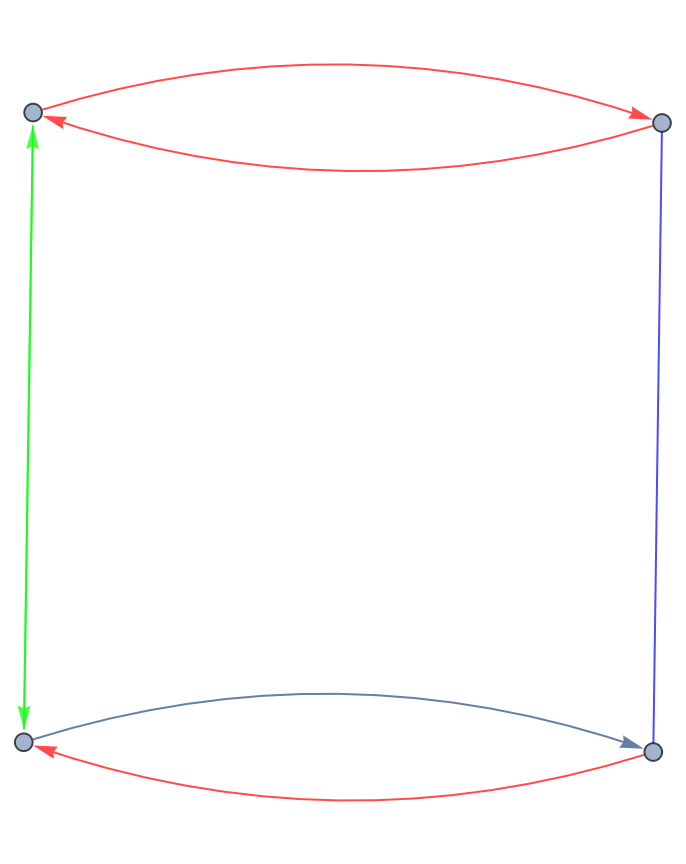 |
Reduce clutter on multiway graphs:
| In[7]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/59704a88-48cf-4dc4-b267-0b7a25557a8c"]](https://www.wolframcloud.com/obj/resourcesystem/images/824/82403039-c8f3-4599-97e3-86afe3939864/24fb0ac6a79d6199.png) |
| In[8]:= |
| Out[8]= | 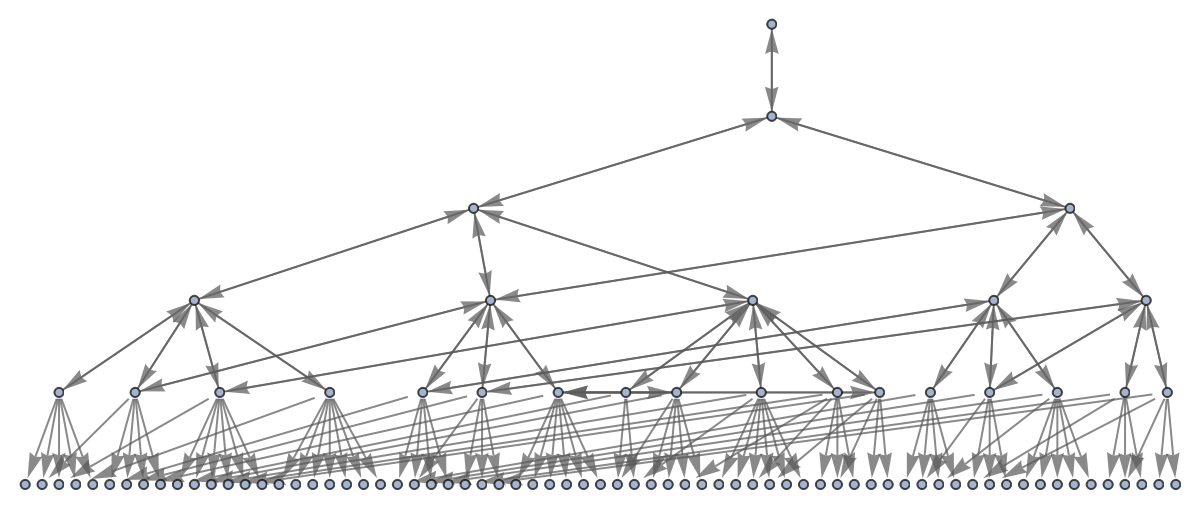 |
This work is licensed under a Creative Commons Attribution 4.0 International License