Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a biarc through two points
ResourceFunction["Biarc"][p1,d1,p2,d2] represents the biarc through the points p1 and p2, with corresponding tangent directions d1 and d2. |
Show a biarc through two points, with given tangent directions:
| In[1]:= |
| Out[1]= |  |
Show biarcs with varying tangent directions:
| In[2]:= | ![Graphics[
Table[{Hue[1 - Rescale[\[Theta], {-\[Pi]/3, \[Pi]/3}]/2], ResourceFunction["Biarc"][{0, 0}, {2, 1}, {1, 0}, AngleVector[\[Theta]]]}, {\[Theta], -\[Pi]/2, \[Pi]/2, \[Pi]/12}],
PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/ed3/ed387d49-eb8b-40f8-b0e0-e47444ec625b/25117c63c05e8bed.png) |
| Out[2]= | 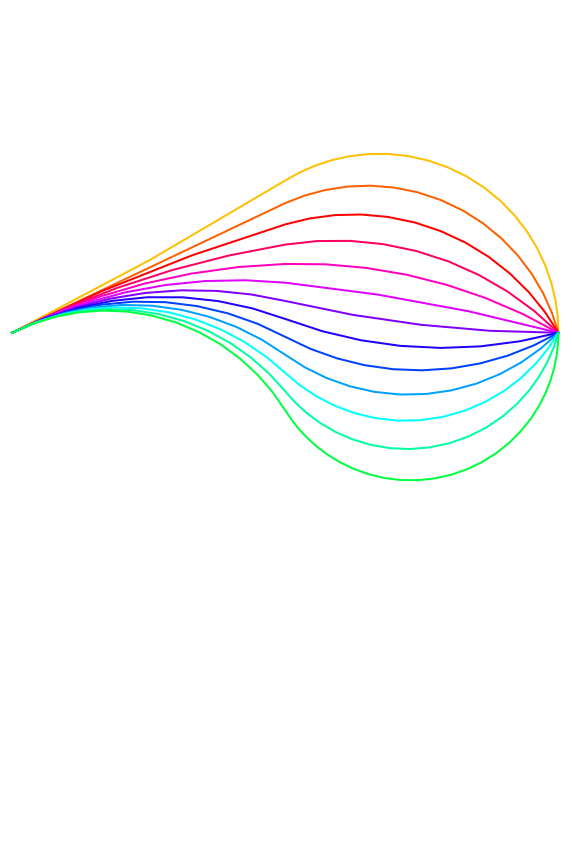 |
Give the circle arcs comprising a biarc:
| In[3]:= |
| Out[3]= |
Show the circle arcs and their corresponding centers along with the biarc:
| In[4]:= | ![Graphics[{{AbsoluteThickness[5], ColorData[97, 1], ResourceFunction[
"Biarc"][{0, 0}, {2, 1}, {1, 0}, {-1, 2}]}, {AbsoluteThickness[2],
AbsolutePointSize[6], Transpose[{{ColorData[97, 4], ColorData[97, 3]}, %, Point[#1] & @@@ %}]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/ed3/ed387d49-eb8b-40f8-b0e0-e47444ec625b/4ce233933c6297c3.png) |
| Out[4]= | 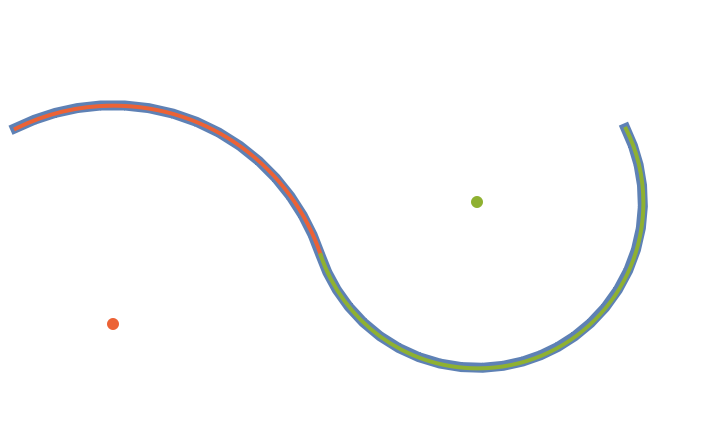 |
Interactively manipulate a biarc:
| In[5]:= | ![Manipulate[
Graphics[{{ColorData[97, 1], AbsoluteThickness[2], ResourceFunction["Biarc"][pt[[1]], pt[[2]] - pt[[1]], pt[[3]], pt[[4]] - pt[[3]]]}, {Arrowheads[Medium], ColorData[97, 4], Arrow[{pt[[1]], pt[[2]]}], Arrow[{pt[[3]], pt[[4]]}]}}, PlotRange -> 4], {{pt, N[{{-2, 0}, {-2, 1}, {2, 0}, {2, 1}}]}, Locator}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/ed3/ed387d49-eb8b-40f8-b0e0-e47444ec625b/152fb265b81d34f1.png) |
| Out[5]= | 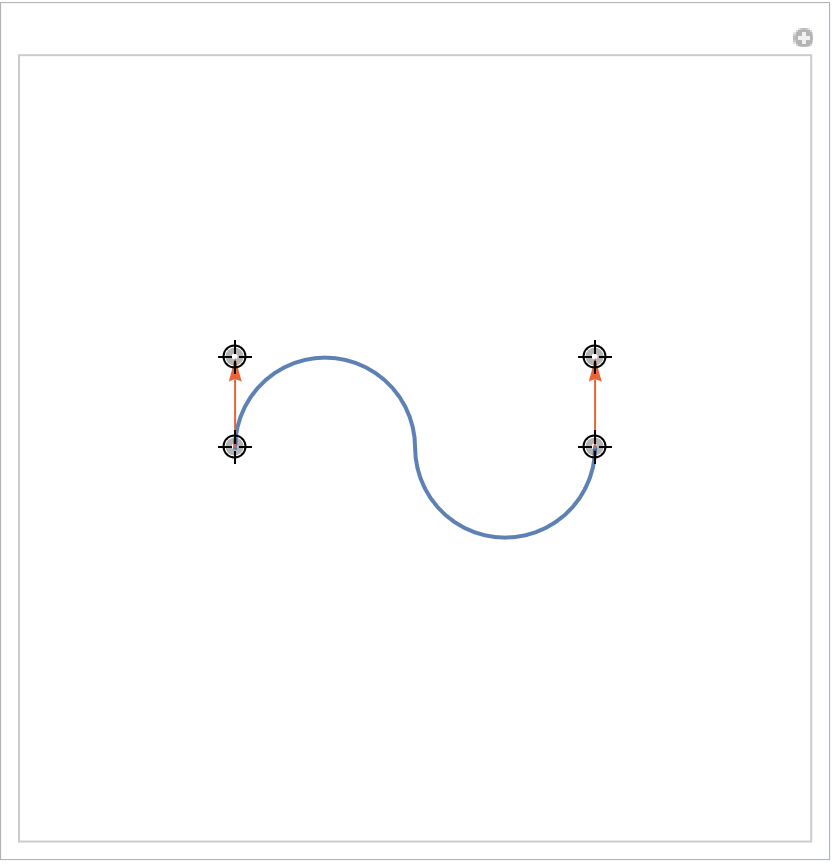 |
This work is licensed under a Creative Commons Attribution 4.0 International License