Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BezierChain

Source Notebook

Create a chain of Bézier curves that smoothly connects a list of points

Contributed by: Mark Greenberg

ResourceFunction["BezierChain"][{p1,p2,…}]

links the points pi with Bézier curves that smoothly flow into each other.

Details and Options

ResourceFunction["BezierChain"][{p1,p2,…}] automatically detects whether the input is 2D or 3D, giving the appropriate output.
ResourceFunction["BezierChain"][{p1,p2,…}] takes the following options:
"Swing"1/3controls the width of curves at the corners; must be greater than 0 and less than or equal to 1
"CurveType""Listed"the type of curve: "Listed", "Joined" or "Filled"

Examples

Basic Examples (2) 

Make a curve that flows through points in 2D:

In[1]:=
pts = {{0, 0}, {1, 1}, {3, 0}, {2, 1}}; Graphics[{ Red, PointSize[Large], Point[pts], Blue, Thick, ResourceFunction["BezierChain"][pts]}]
Out[2]=

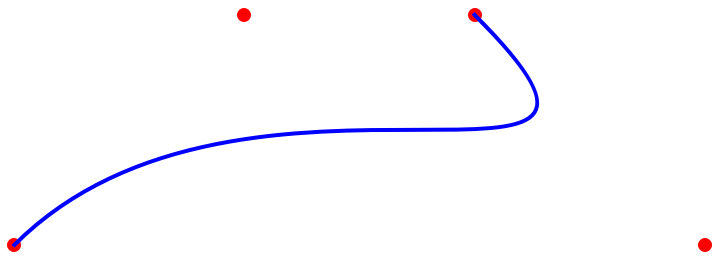
In contrast, an ordinary Bézier curve will not go through all the control points:

In[3]:=
Graphics[{ Red, PointSize[Large], Point[pts], Blue, Thick, BezierCurve[pts]}]
Out[3]=

Scope (1) 

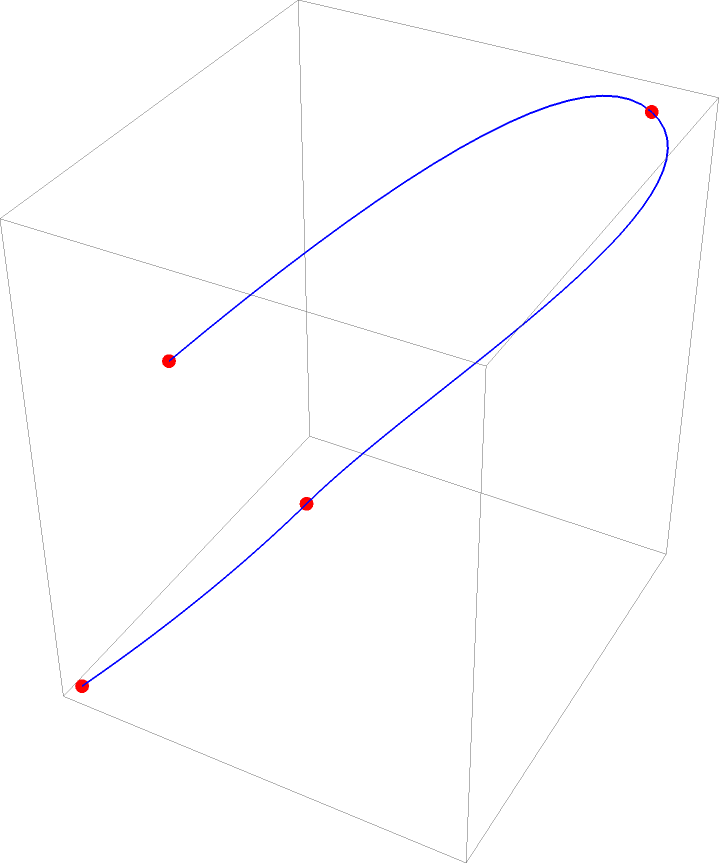
Make a curve that flows through points in 3D:

In[4]:=
pts = Partition[RandomReal[{-1, 1}, 12], 3]; Graphics3D[{ Red, PointSize[Large], Point[pts], Blue, Thick, ResourceFunction["BezierChain"][pts]}]
Out[5]=

Options (4) 

CurveType (1) 

The "CurveType" option changes the type of 2D curve returned:

In[6]:=
pt = {{0, 0}, {1, 1}, {3, 0}, {2, 1}}; l = Graphics[ Arrow[#] & /@ ResourceFunction["BezierChain"][pt, CurveType -> "Listed"]]; j = Graphics[ Arrow[ResourceFunction["BezierChain"][pt, CurveType -> "Joined"]]]; f = Graphics[ ResourceFunction["BezierChain"][pt, CurveType -> "Filled"]]; {l, j, f}
Out[10]=

Swing (3) 

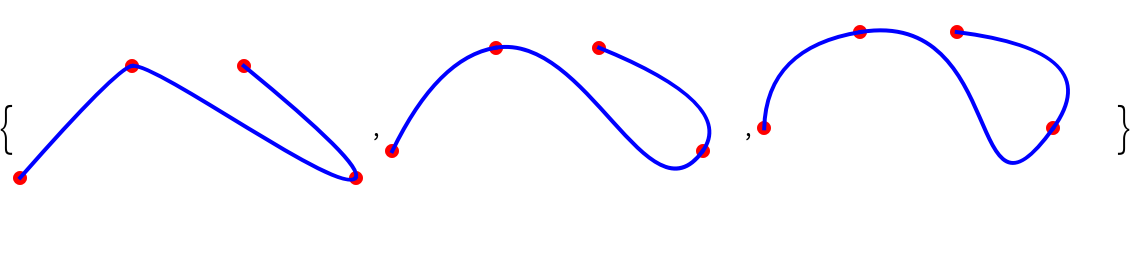
The "Swing" option, which has an effective range of 0<n≤1, controls how curvy the connection is between Bézier sections:

In[11]:=
pts = {{0, 0}, {1, 1}, {3, 0}, {2, 1}}; Table[Graphics[{ Red, PointSize[Large], Point[pts], Blue, Thick, ResourceFunction["BezierChain"][pts, "Swing" -> s]}, ImageSize -> Small], {s, {.1, .4, .7}}]
Out[12]=

A swing value of 0 is equivalent to using Line:

In[13]:=
pt = {{0, 0}, {1, 1}, {3, 0}, {2, 1}}; {Graphics[ResourceFunction["BezierChain"][pt, "Swing" -> 0]], Graphics[Line[pt]]}
Out[14]=

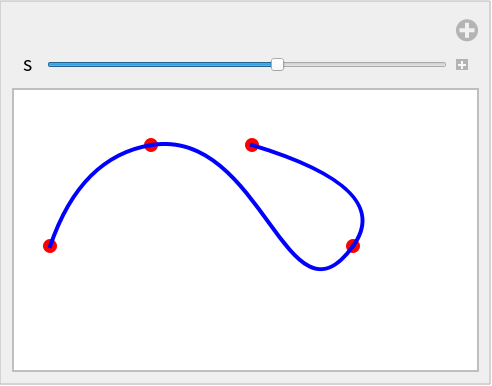
Dynamically adjust the swing value:

In[15]:=
pt = {{0, 0}, {1, 1}, {3, 0}, {2, 1}}; Manipulate[ Graphics[{ Red, PointSize[Large], Point[pt], Blue, Thick, ResourceFunction["BezierChain"][pt, "Swing" -> s]}, ImageSize -> Small], {{s, .5}, -3, 3}, SaveDefinitions -> True]
Out[16]=

Possible Issues (1) 

If the first and last points coincide (to make it a closed curve), they will not be smoothly connected, but instead will show a cusp:

In[17]:=
pts = {{0, 0}, {1, 1}, {3, 0}, {2, 1}, {0, 0}}; Graphics[{ Red, PointSize[Large], Point[pts], Blue, Thick, ResourceFunction["BezierChain"][pts]}]
Out[18]=

Applications (2) 

Trace a path in 2D or 3D space:

In[19]:=
Graphics3D[{ Cylinder[{{0, 0, 1}, {0, 0, 4}}, .25], Cylinder[{{0, 0, 0}, {0, 0, 2}}], Cylinder[{{3, 0, 0}, {3, 0, 3}}, .25], Cylinder[{{3, 0, 2}, {3, 0, 4}}], Blue, Thick, ResourceFunction[ "BezierChain"][{{-2, 1, 3}, {0, -1, 3}, {1.5, 0, 2}, {3, 1, 1}, {5, -1, 1}}] }]
Out[19]=

Make the points dynamic, as in this Manipulate:

In[20]:=
Manipulate[ pts = {{0, 0}, {1, 1}, pt3, {2, 1}}; Graphics[{Blue, ResourceFunction["BezierChain"][pts]}, PlotRange -> {{0, 4}, {-2, 2}}], {{pt3, {3, 0}}, Locator}, SaveDefinitions -> True]
Out[20]=

Neat Examples (2) 

Simulate handwriting:

In[21]:=
pt = {{{0, 0}, {4, 5.2}, {5.2, 9}, {2, 0}}, {{2, 0}, {3.9, 3.7}, {5, 0}, {6.5, .2}}}; Graphics[{Thick, Darker[Blue], ResourceFunction["BezierChain"][pt[[1]], "Swing" -> .2], ResourceFunction["BezierChain"][pt[[2]]]}, ImageSize -> Small]
Out[22]=

Braid tubes:

In[23]:=
pts = {{{0, -0.5, -0.3}, {2, -1, 0}, {4, -0.5, 0.3}, {6, 0.5, -0.3}, { 8, 1, 0}, {10, 0.5, 0.3}, {12, -0.5, -0.3}}, {{0, -0.5, 0.3}, { 2, 0.5, -0.3}, {4, 1, 0}, {6, 0.5, 0.3}, {8, -0.5, -0.3}, {10, -1, 0}, {12, -0.5, 0.3}}, {{0, 1, 0}, {2, 0.5, 0.3}, { 4, -0.5, -0.3}, {6, -1, 0}, {8, -0.5, 0.3}, {10, 0.5, -0.3}, {12, 1, 0}}}; bez = ResourceFunction["BezierChain"][#] /. a_BezierCurve -> Tube[a, .6] & /@ pts; Graphics3D[Riffle[{Cyan, White, LightYellow}, bez]]
Out[25]=

Publisher

Mark Greenberg

Version History

  • 1.1.0 – 10 March 2021
  • 1.0.0 – 25 January 2021

Related Resources

License Information