Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BaxterPermutationQ

Source Notebook

Determine whether a permutation is a Baxter permutation

Contributed by: Motoharu Ito

ResourceFunction["BaxterPermutationQ"][perm]

gives True if perm is a Baxter permutation and False otherwise.

Details

A permutation p={p1,p2,…,pn} is a Baxter permutation if there are no four indices i<j<k<l such that k=j+1 and pi,pj,pk,pl is an occurrence of the pattern 2413 or 3142.

Examples

Basic Examples (2) 

Test whether {2,6,3,1,5,4} is a Baxter permutation:

In[1]:=
ResourceFunction["BaxterPermutationQ"][{2, 6, 3, 1, 5, 4}]
Out[1]=

{2,4,1,3} is not a Baxter permutation:

In[2]:=
ResourceFunction["BaxterPermutationQ"][{2, 4, 1, 3}]
Out[2]=

{2,5,4,1,3} is not a Baxter permutation because it does not avoid pattern 2413 for (i,j,k,l)=(1,3,4,5):

In[3]:=
ResourceFunction["BaxterPermutationQ"][{2, 5, 4, 1, 3}]
Out[3]=

{1,3,5,2,4} is not a Baxter permutation because it does not avoid pattern 2413 for (i,j,k,l)=(2,3,4,5):

In[4]:=
ResourceFunction["BaxterPermutationQ"][{1, 3, 5, 2, 4}]
Out[4]=

Scope (2) 

Count the total number of Baxter permutations up to length seven (the Baxter numbers):

In[5]:=
Table[Count[ ResourceFunction["BaxterPermutationQ"] /@ NestList[ResourceFunction["NextPermutation"], Range[k], k! - 1], True], {k, 0, 7}]
Out[5]=

Compare with an explicit expression for the Baxter numbers:

In[6]:=
Table[HypergeometricPFQ[{-1 - k, -k, 1 - k}, {2, 3}, -1], {k, 0, 7}]
Out[6]=

The permutations of the down-crossing fixed points is a Baxter Permutation:

In[7]:=
n = 8; \[Epsilon] = 0.001; h[x_] := ChebyshevT[n, x]; fp = Sort[SolveValues[h[x] == x, x], Less]; downfp = N[Select[fp, (D[h[x] - x, x] /. x -> #) < 0 &]]; rule[k_] := x_ /; IntervalMemberQ[ Interval[{downfp[[k]] - \[Epsilon], downfp[[k]] + \[Epsilon]}], x] -> k; rules = Table[rule[k], {k, 1, Length[downfp]}]; Table[Fold[ReplaceAll, ChebyshevT[k, downfp], rules], {k, Divisors[n]}]
Out[8]=
In[9]:=
ResourceFunction["BaxterPermutationQ"] /@ %
Out[9]=

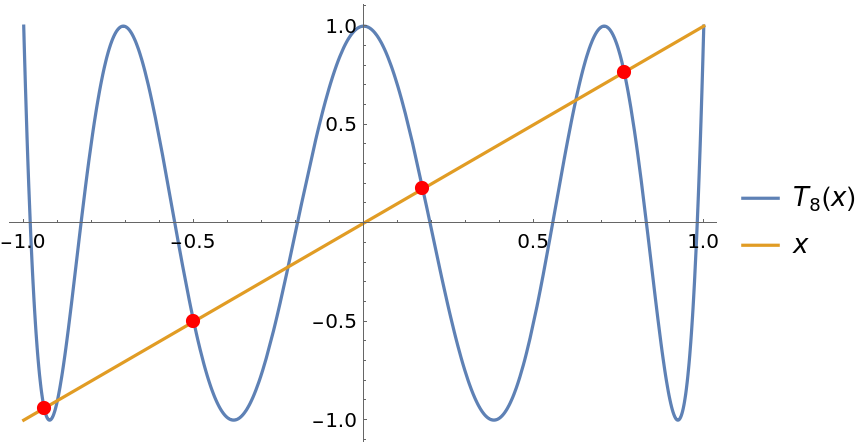
If the positive integers n, a, b have n=ab, then the Chebyshev polynomial satisfies Tn=TaTb=TbTa. Then Tn(Ta(x))=Ta(Tn(x))=Ta(x), so Ta(x) is also a fixed point of Tn. Similarly, Tb(x) is also a fixed point of Tn. Thus, Ta and Tb are fixed point permutations on the fixed point set of Tn. Interestingly, the permutation by Ta and Tb also preserves the type of fixed points (i.e. up-crossing, down-crossing, touching). The type is the mapping of a down-crossing fixed point to a down-crossing fixed point. The fixed points marked with red dots are down-crossing fixed points:

In[10]:=
Plot[{h[x], x}, {x, -1, 1}, Epilog -> {PointSize[0.02], Red, Point[Map[{#, h[#]} &, downfp]]}, PlotLegends -> {Subscript[T, n][x], x}]
Out[10]=

Publisher

Motoharu Ito

Version History

  • 1.0.0 – 08 December 2022

Source Metadata

  • Citation:
    Kitaev S., Patterns in Permutations and Words. Springer, 2013.

Related Resources

License Information