Basic Examples (2) 

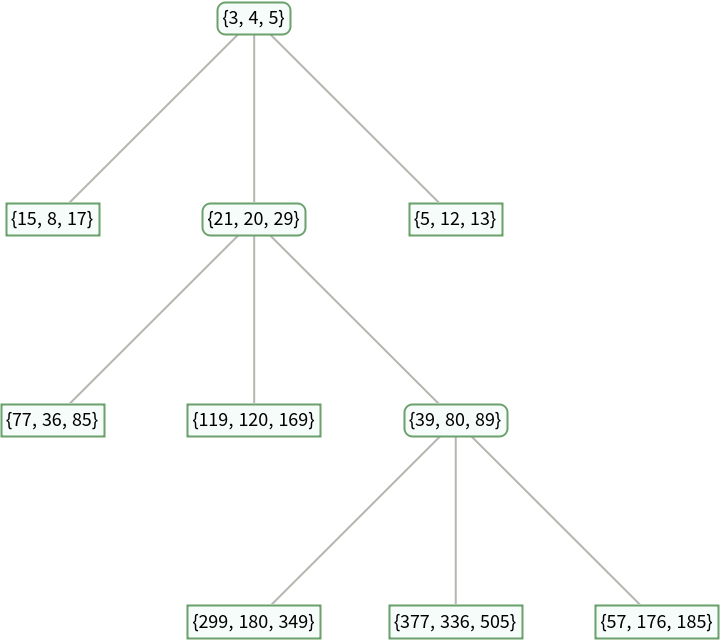
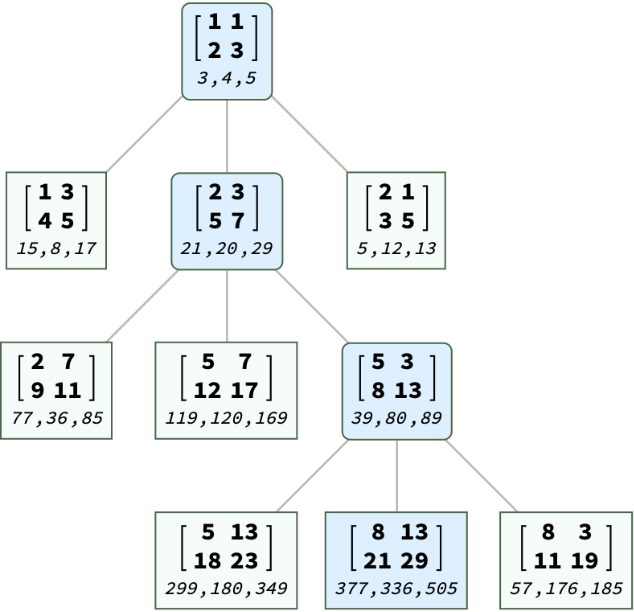
Given a primitive Pythagorean triple, find its position on the Barning-Hall tree:

In[1]:=

Out[2]=

See the tree:

In[3]:=

Out[3]=

Scope (2) 

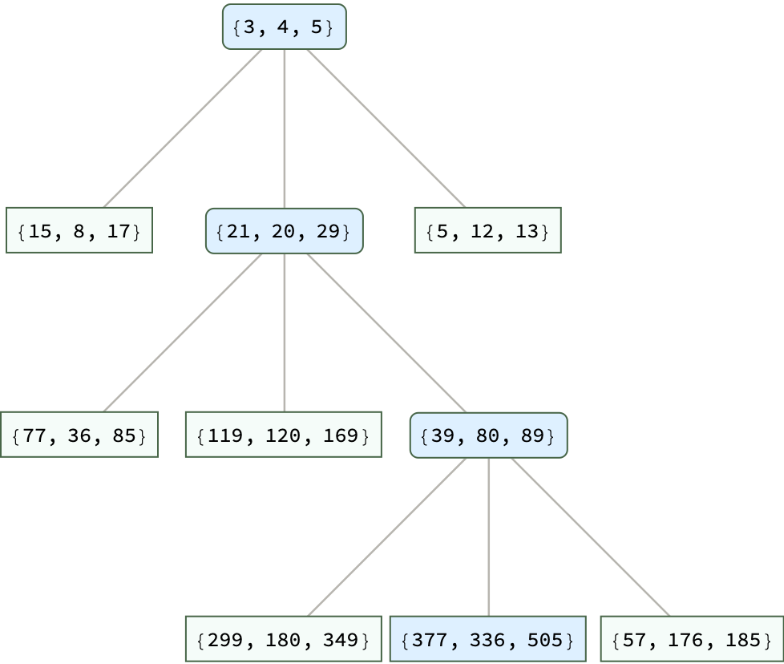
Use "PathWithFibonacciPythagoreanPair" to show the tree withFibonacci matrices from the root node to the target:

In[4]:=

Out[5]=

Use "PathWithPythagoreanTriple" to show the tree from root node to the target with Fibonacci matrices:

In[6]:=

Out[8]=

Properties and Relations (3) 

BarningHallTreePosition with "PathWithFibonacciPythagoreanPair" automatically aligns the Pythagorean triples vertically in the node to minimize the width of each node as the triples grows rapidly:

In[9]:=

Out[11]=

"PathWithPythagoreanTriple" saves raw data therefore no automatic formatting implemented:

In[12]:=

Out[14]=

Use TreeMap and Column or TableForm function to convert the tree into more compact and legible form:

In[15]:=

Out[15]=

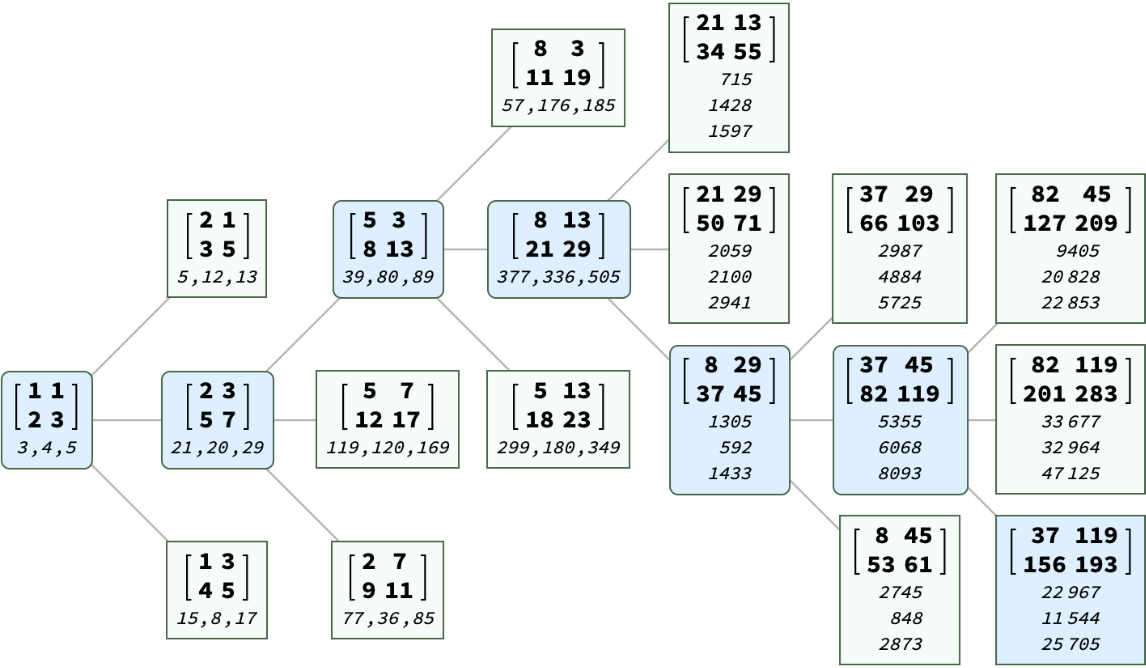
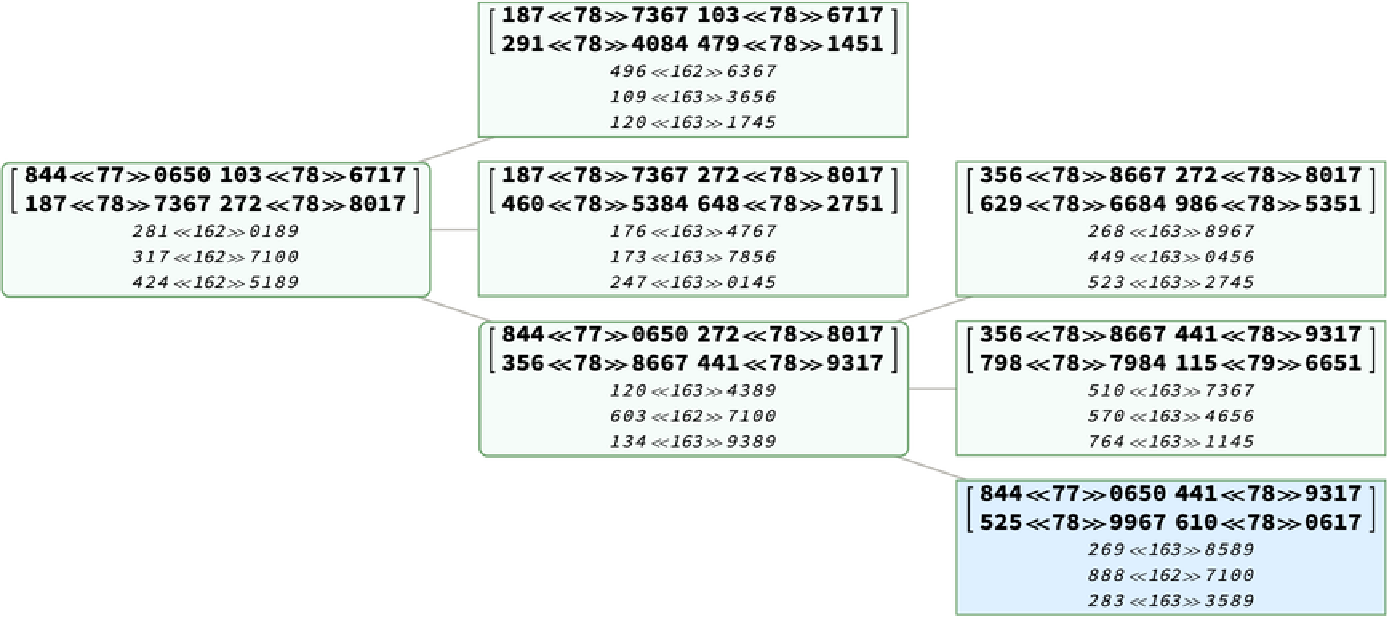
BarningHallTreePosition properly handles the display of gigantic Pythagorean triples with deep tree levels using the Format function internally. Together with TreeExtract and TreeElementStyle we can create a neat subtree. Specify a Pythagorean triple with huge values:

In[16]:=

Each number is close to 170 digits:

In[17]:=

Out[17]=

The path on the tree has 300 levels of depth and would not be a useful visualization:

In[18]:=

Out[20]=

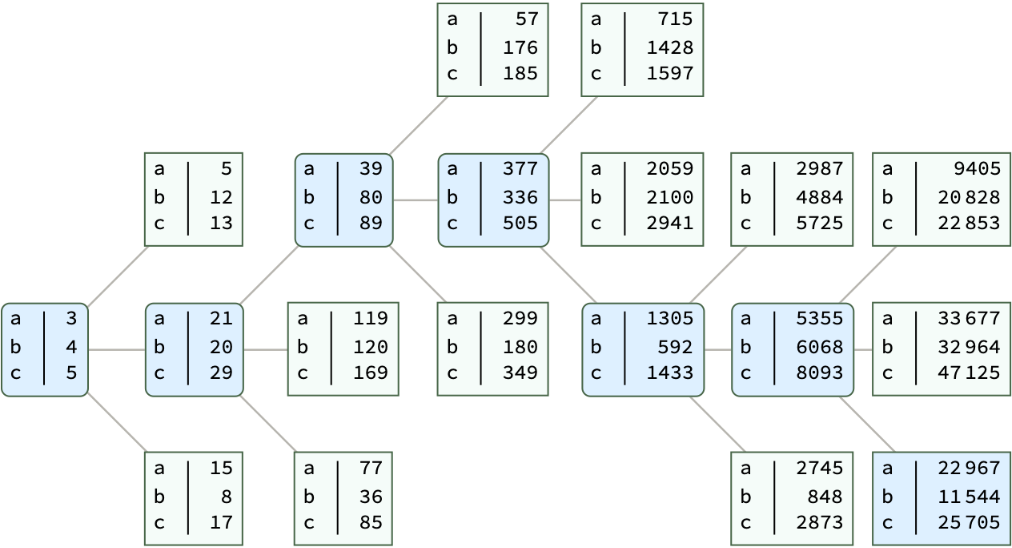
Take the last three levels including the target input on the tree:

In[21]:=

Customize the coordinate for the tree nodes to arrange the sibling, parents and grandparent node for the input:

In[22]:=

Out[22]=

Possible Issues (3) 

The input must be Pythagorean triple. For instance {5,12,14} is not Pythagorean. The function returns unevaluated:

In[23]:=

Out[23]=

The Pythagorean triple must be primitive. For instance {5,12,13} with GCD[5,12,13] = 1. {10,24,26} is Pythagorean but not primitive. The input yields unevaluated form:

In[24]:=

Out[24]=

The function uses canonical primitive Pythagorean triple notation as it is compatible with its intermediate triples. Changing the sequence of the input results in an unevaluated result:

In[25]:=

Out[25]=

Neat Examples (8) 

Schinzel’s hypothesis H implies that there are infinite number of primitive Pythagorean triples with two primes. This requires that both odd leg a and odd hypotenuse 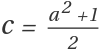being prime number and the length of the even leg is one less than that of the hypotenuse. Let's take a look at the example:

In[26]:=

Out[27]=

Solve for the Pythagorean equation and notice that b is one less than c:

In[28]:=

Out[28]=

Actually, given such c, the other two variables are determined in this Diophantine equation:

In[29]:=

Out[29]=

For other cases, we choose prime p such that 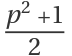is also a prime number:

In[30]:=

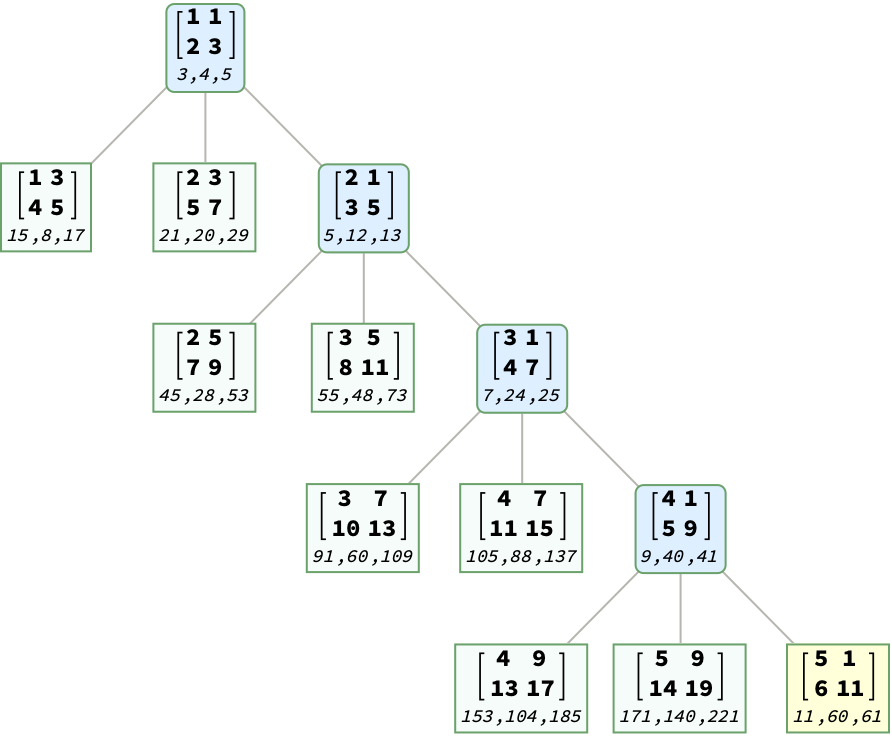
Pick 5 elements and we can check the location of the triples on the tree with obvious pattern:

In[31]:=

Out[31]=

For instance, we can visualize the {11,60,61} on the B-H tree:

In[32]:=

Out[33]=

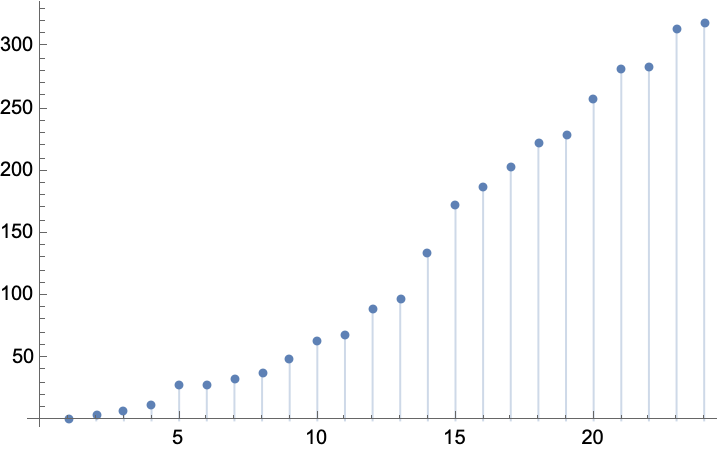
The number of 3's in each position for primitive Pythagorean triple with two primes defines an interesting sequence. The sequence is A068501 with each term minus one:

In[34]:=

Out[35]=

Plot the curve of the sequence:

In[36]:=

Out[36]=

Notice that the tree position of repeating 3's is just a necessary condition for Pythagorean triple to have 2 primes. (7,24,25) is at {3,3} and 25 is not prime. In fact, the tree position of repeating 3's is sufficient and necessary condition for primitive Pythagorean triple with (a,c-1,c) form in our Barning-Hall tree convention. Those triples with two primes are strictly in the subset of the (a,c-1,c) cases.