Basic Examples (2)
Given a primitive Pythagorean triple, find its position on the Barning-Hall tree:
See the tree:
Scope (2)
Use "PathWithFibonacciPythagoreanPair" to show the tree withFibonacci matrices from the root node to the target:
Use "PathWithPythagoreanTriple" to show the tree from root node to the target with Fibonacci matrices:
Properties and Relations (3)
BarningHallTreePosition with "PathWithFibonacciPythagoreanPair" automatically aligns the Pythagorean triples vertically in the node to minimize the width of each node as the triples grows rapidly:
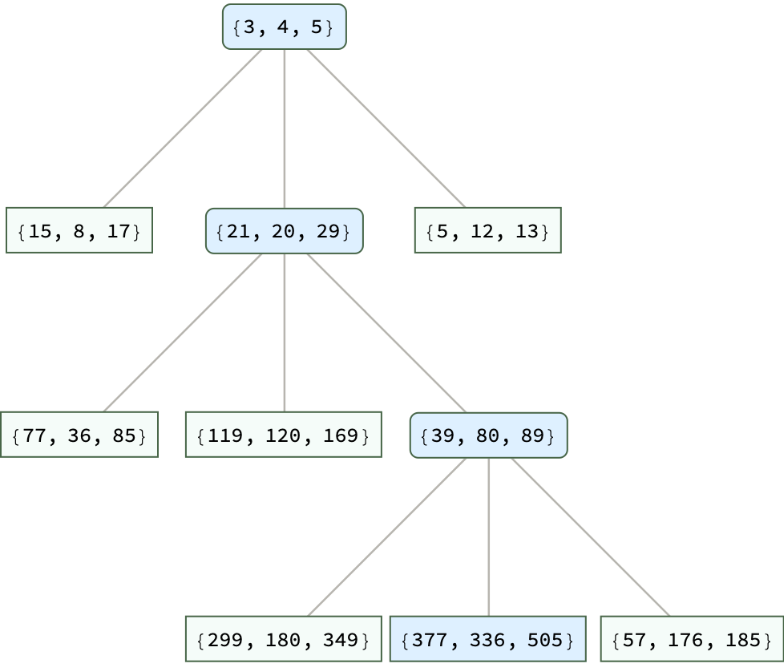
"PathWithPythagoreanTriple" saves raw data therefore no automatic formatting implemented:
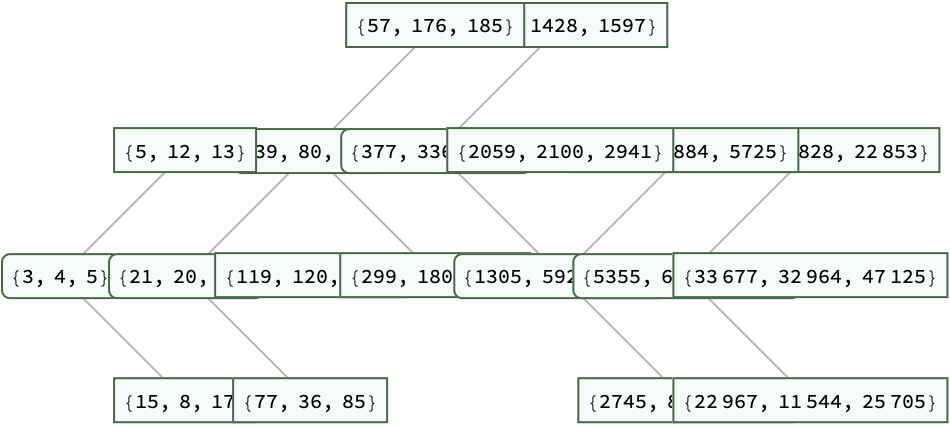
Use TreeMap and Column or TableForm function to convert the tree into more compact and legible form:
BarningHallTreePosition properly handles the display of gigantic Pythagorean triples with deep tree levels using the Format function internally. Together with TreeExtract and TreeElementStyle we can create a neat subtree. Specify a Pythagorean triple with huge values:
Each number is close to 170 digits:
The path on the tree has 300 levels of depth and would not be a useful visualization:
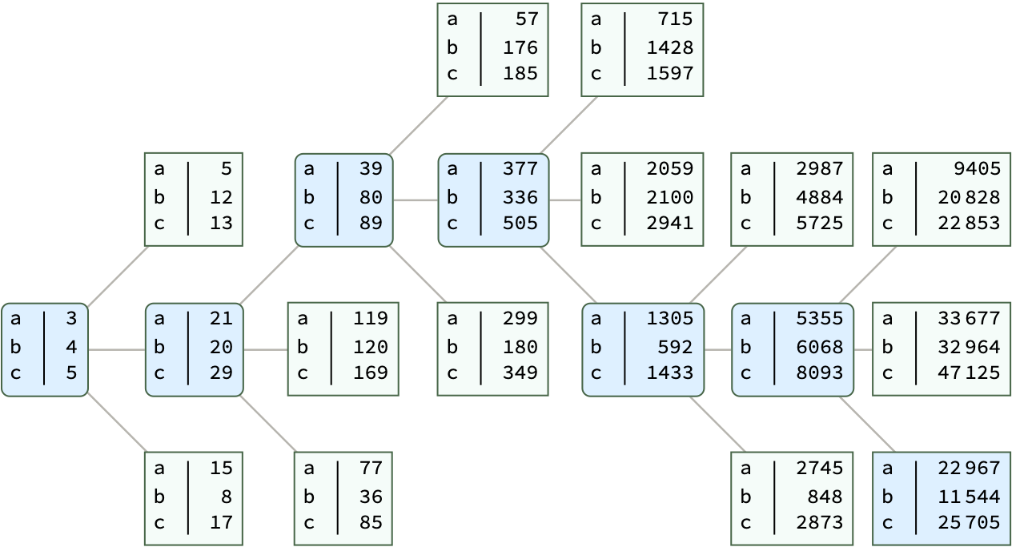
Take the last three levels including the target input on the tree:
Customize the coordinate for the tree nodes to arrange the sibling, parents and grandparent node for the input:
Possible Issues (3)
The input must be Pythagorean triple. For instance {5,12,14} is not Pythagorean. The function returns unevaluated:
The Pythagorean triple must be primitive. For instance {5,12,13} with GCD[5,12,13] = 1. {10,24,26} is Pythagorean but not primitive. The input yields unevaluated form:
The function uses canonical primitive Pythagorean triple notation as it is compatible with its intermediate triples. Changing the sequence of the input results in an unevaluated result:
Neat Examples (8)
Schinzel’s hypothesis H implies that there are infinite number of primitive Pythagorean triples with two primes. This requires that both odd leg a and odd hypotenuse 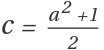 being prime number and the length of the even leg is one less than that of the hypotenuse. Let's take a look at the example:
being prime number and the length of the even leg is one less than that of the hypotenuse. Let's take a look at the example:
Solve for the Pythagorean equation and notice that b is one less than c:
Actually, given such c, the other two variables are determined in this Diophantine equation:
For other cases, we choose prime p such that 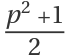 is also a prime number:
is also a prime number:
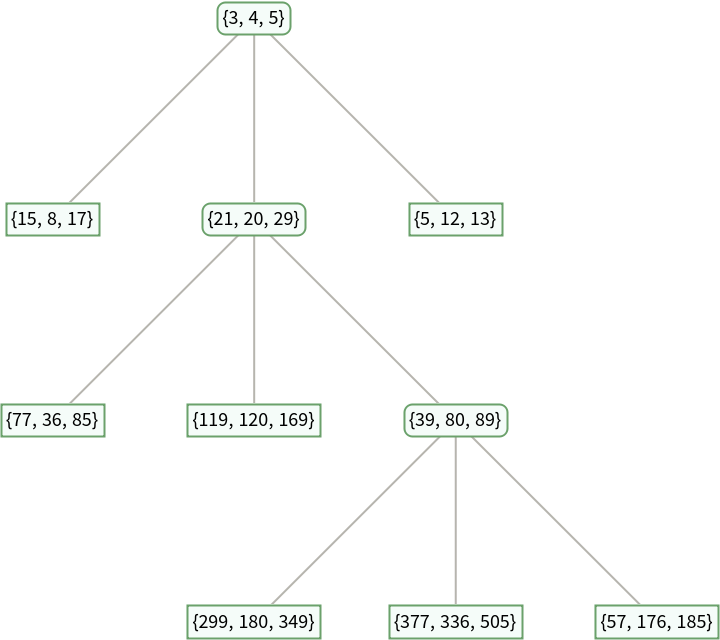
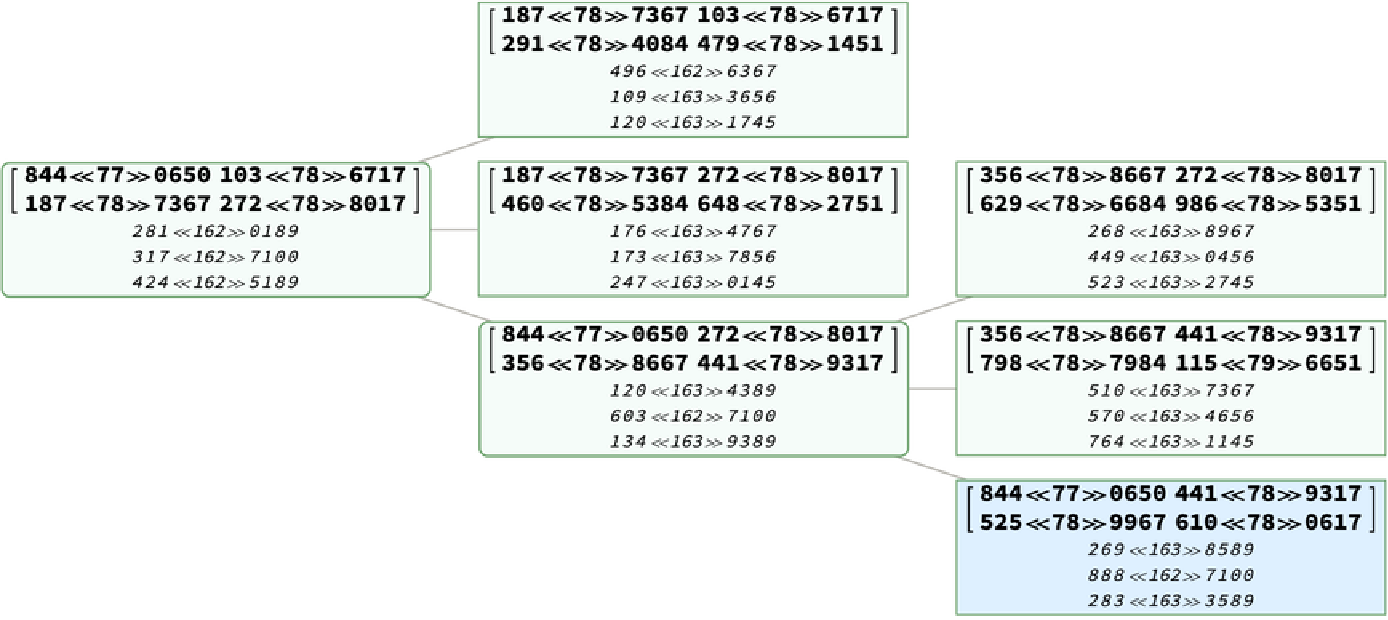
Pick 5 elements and we can check the location of the triples on the tree with obvious pattern:
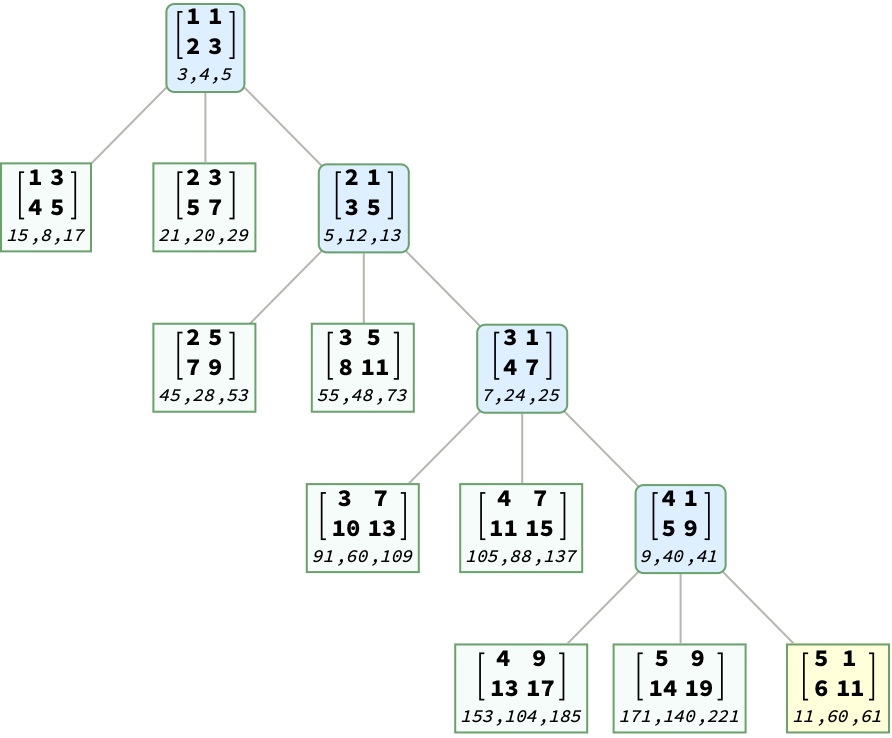
For instance, we can visualize the {11,60,61} on the B-H tree:
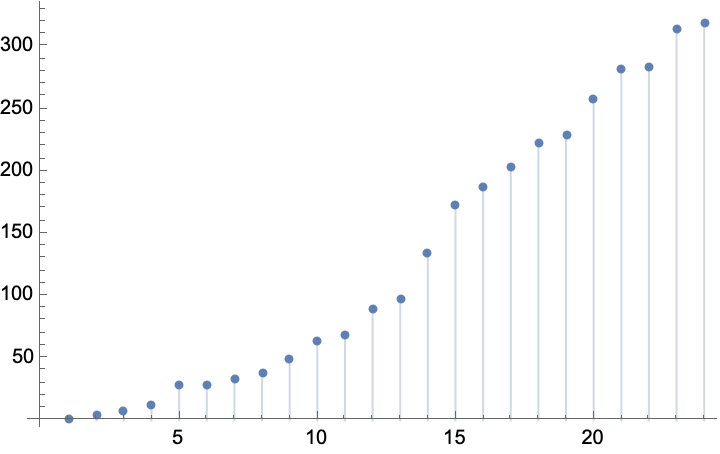
The number of 3's in each position for primitive Pythagorean triple with two primes defines an interesting sequence. The sequence is A068501 with each term minus one:
Plot the curve of the sequence:
Notice that the tree position of repeating 3's is just a necessary condition for Pythagorean triple to have 2 primes. (7,24,25) is at {3,3} and 25 is not prime. In fact, the tree position of repeating 3's is sufficient and necessary condition for primitive Pythagorean triple with (a,c-1,c) form in our Barning-Hall tree convention. Those triples with two primes are strictly in the subset of the (a,c-1,c) cases.
![ppt = {377, 336, 505};
pos = ResourceFunction["BarningHallTreePosition"][ppt];
Tree[
ResourceFunction["BarningHallTreePosition"][ppt, "PathWithFibonacciPythagoreanPair"],
TreeElementStyle -> ((# -> LightBlue) & /@ FoldList[Flatten@{##} &, {}, pos])]](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/3d7c1fca9c8ae8d8.png)
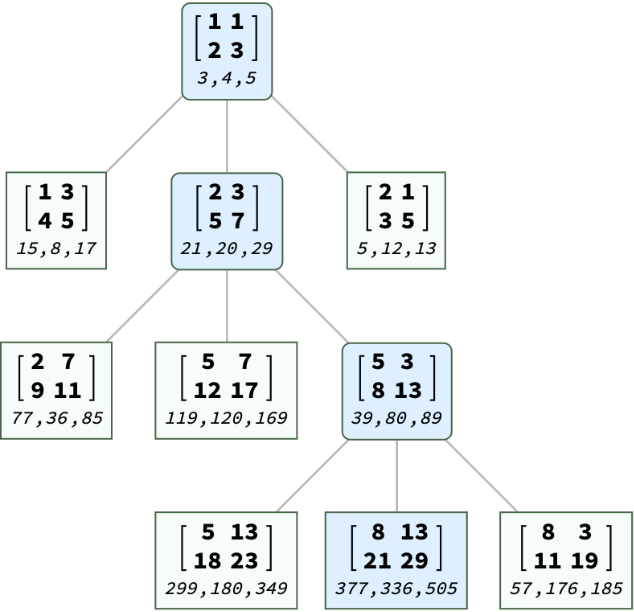
![ppt = {377, 336, 505};
pos = ResourceFunction["BarningHallTreePosition"][ppt];
Tree[
ResourceFunction["BarningHallTreePosition"][ppt, "PathWithPythagoreanTriple"],
TreeElementStyle -> ((# -> LightBlue) & /@ FoldList[Flatten@{##} &, {}, pos])]](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/12aa9564df8e106a.png)
![ppt = {22967, 11544, 25705};
pos = ResourceFunction["BarningHallTreePosition"][ppt];
Tree[ResourceFunction["BarningHallTreePosition"][ppt, "PathWithFibonacciPythagoreanPair"], TreeLayout -> Left, TreeElementStyle -> ((# -> LightBlue) & /@ FoldList[Flatten@{##} &, {}, pos])]](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/6bfe21bb1d2a5cde.png)
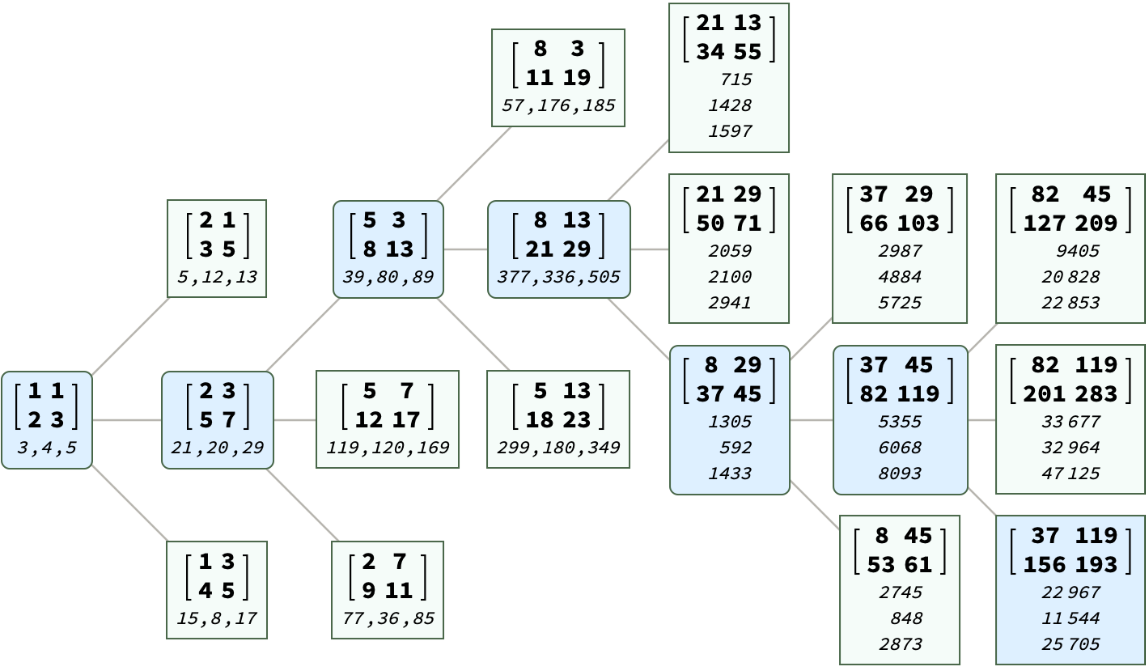
![ppt = {22967, 11544, 25705};
pos = ResourceFunction["BarningHallTreePosition"][ppt];
res = Tree[
ResourceFunction["BarningHallTreePosition"][ppt, "PathWithPythagoreanTriple"], TreeLayout -> Left]](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/4347e9cd30d239c7.png)
![Tree[
TreeMap[
TableForm[Transpose[{#}], TableHeadings -> {{"a", "b", "c"}, None}, TableAlignments -> Right] &, res],
TreeElementStyle -> ((# -> LightBlue) & /@ FoldList[Flatten@{##} &, {}, pos]),
TreeLayout -> Left
]](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/3c0a66f3806bbf1d.png)
![lastNLevels = 3;
pos4 = ResourceFunction["BarningHallTreePosition"][ppt];
{Length[pos4], Short[pos4]}](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/668903e20170b5fb.png)
![res = TreeExtract[
ResourceFunction["BarningHallTreePosition"][ppt, "PathWithFibonacciPythagoreanPair"], pos4[[;; -lastNLevels]]];](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/25b370216925de7b.png)
![Tree[res,
TreeElementStyle -> {pos4[[-lastNLevels + 1 ;;]] -> LightBlue},
TreeElementCoordinates -> {
{} -> {0, 1/3},
{1} -> {1, 0}, {2} -> {1, 1/3}, {3} -> {1, 2/3},
{1, 1} -> {2, -1/3}, {1, 2} -> {2, 0}, {1, 3} -> {2, 1/3}}]](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/55e25f099e7a758f.png)
![]() being prime number and the length of the even leg is one less than that of the hypotenuse. Let's take a look at the example:
being prime number and the length of the even leg is one less than that of the hypotenuse. Let's take a look at the example:![(* https://oeis.org/A048161 *)
a = 1901;
c = (a^2 + 1)/2;
{c, PrimeQ[c], PrimeQ[a]}](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/1d1938e21c0f9309.png)
![]() is also a prime number:
is also a prime number:![candidates = Select[Prime[Range[120]], PrimeQ[(#^2 + 1)/2] &];
trps = Module[{a = #, c}, c = (a^2 + 1)/2; {a, c - 1, c}] & /@ candidates;](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/3173e339e3fdfcf4.png)
![ResourceFunction["NiceGrid"][MapThread[
<|"Primitive Pythagorean Triple" -> #1, "Position" -> #2|> &,
{Rest[trps[[;; 6]]], Rest[ResourceFunction["BarningHallTreePosition"][#] & /@ trps][[;; 5]]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/46f973b7ff4aeaff.png)

![pos = {3, 3, 3, 3};
pathLoc = (# -> LightBlue) & /@ FoldList[Flatten[{##}] &, {}, Rest[pos]];
Tree[ResourceFunction[
"BarningHallTreePosition"][\!\(TraditionalForm\`{11, 60, 61}\), "PathWithFibonacciPythagoreanPair"],
TreeElementStyle -> {Splice@pathLoc, pos -> LightYellow}]](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/61f98fedd86228fa.png)
![data = Length /@ Rest[ResourceFunction["BarningHallTreePosition"][#] & /@ trps];
Column@{data, ResourceFunction[
ResourceObject[<|"Name" -> "OEISSequence", "ShortName" -> "OEISSequence", "UUID" -> "12010764-9f22-4e11-9ecf-3310f9f9e7d4", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Return the list provided by the OEIS for a given OEIS sequence number", "RepositoryLocation" -> URL[
"https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$83e5783b1cb54fb8a9f1819c50935826`OEISSequence", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/bb406b01-d308-49cc-9402-42e3af604c25"]|>, ResourceSystemBase -> Automatic]]["A068501"][[
2 ;; 25]] - 1}](https://www.wolframcloud.com/obj/resourcesystem/images/469/4692d523-402c-4f51-a6f0-65359413f1d2/1d53e77a8273acc1.png)