Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BalabanJ

Source Notebook

Compute the Balaban J index of an undirected graph or a molecule

Contributed by: Jan Mangaldan

ResourceFunction["BalabanJ"][g]

computes the Balaban J index of the graph g.

ResourceFunction["BalabanJ"][mol]

computes the Balaban J index of the Molecule expression mol.

Details

The Balaban J index is also known as the Balaban distance connectivity index or the average distance sum connectivity.
For an undirected, connected graph with e edges and v vertices, the Balaban index is defined as , where di is the ith row sum of the graph distance matrix and the sum ranges over all edges of the graph.
ResourceFunction["BalabanJ"][mol] computes the Balaban J index of a molecule mol, where the molecule is treated as an edge-weighted graph with weights equal to the reciprocal of the bond order and the hydrogens are ignored by default. Use the option setting IncludeHydrogens→All to account for hydrogens.
ResourceFunction["BalabanJ"][entity] computes the Balaban J index of an entity of type "Chemical" or "Graph".

Examples

Basic Examples (2) 

The Balaban index of a Petersen graph:

In[1]:=
ResourceFunction["BalabanJ"][PetersenGraph[]]
Out[1]=

Get the same result from GraphData:

In[2]:=
GraphData["PetersenGraph", "BalabanIndex"]
Out[2]=

Scope (4) 

Compute the Balaban indices of the order-1 buckyball graph of different classes:

In[3]:=
ResourceFunction[ "BalabanJ"] /@ {BuckyballGraph[1, "I"], BuckyballGraph[1, "II"]}
Out[3]=

Compute the Balaban indices of two different molecules:

In[4]:=
ResourceFunction[ "BalabanJ"] /@ {Molecule["cyclohexane"], Molecule["benzene"]}
Out[4]=

Compute the Balaban index of a named entity:

In[5]:=
ResourceFunction["BalabanJ"][Entity["Graph", "TietzeGraph"]]
Out[5]=

Compute the Balaban index of the Balaban graph:

In[6]:=
ResourceFunction["BalabanJ"][Entity["Graph", "Balaban10Cage"]]
Out[6]=

Options (2) 

IncludeHydrogens (2) 

By default, hydrogens are ignored in the computation of the Balaban index:

In[7]:=
ResourceFunction["BalabanJ"][Molecule["neopentane"]]
Out[7]=

Use IncludeHydrogens→All to account for hydrogens:

In[8]:=
ResourceFunction["BalabanJ"][Molecule["neopentane"], IncludeHydrogens -> All]
Out[8]=

Applications (2) 

A list of straight-chain alkanes:

In[9]:=
alkanes = {Entity["Chemical", "Propane"], Entity["Chemical", "Butane"], Entity["Chemical", "Pentane"], Entity["Chemical", "Hexane"], Entity["Chemical", "Heptane"], Entity["Chemical", "Octane"], Entity["Chemical", "Nonane"], Entity["Chemical", "Decane"], Entity["Chemical", "Undecane"], Entity["Chemical", "Dodecane"]};

Get their corresponding boiling points:

In[10]:=
bp = QuantityMagnitude[EntityValue[#, "BoilingPoint"] & /@ alkanes, "Kelvins"]
Out[10]=

Get their Balaban indices:

In[11]:=
ji = ResourceFunction["BalabanJ"] /@ alkanes
Out[11]=

The Balaban index is strongly correlated with the logarithm of the boiling point. Visualize the trend:

In[12]:=
ListLogPlot[Transpose[{ji, bp}], Joined -> True, PlotMarkers -> Automatic]
Out[12]=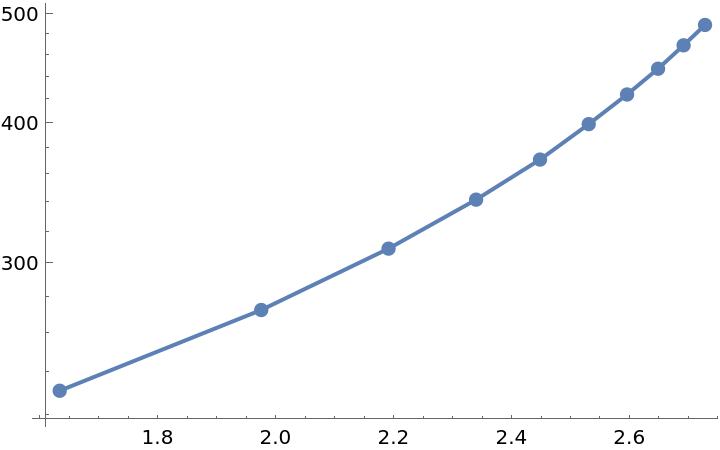

Compute the correlation coefficient:

In[13]:=
Correlation[ji, Log[bp]]
Out[13]=

Generate all alkanes with 7 carbon atoms (heptanes) using the resource function AlkaneIsomers:

In[14]:=
heptanes = ResourceFunction["AlkaneIsomers"][7]
Out[14]=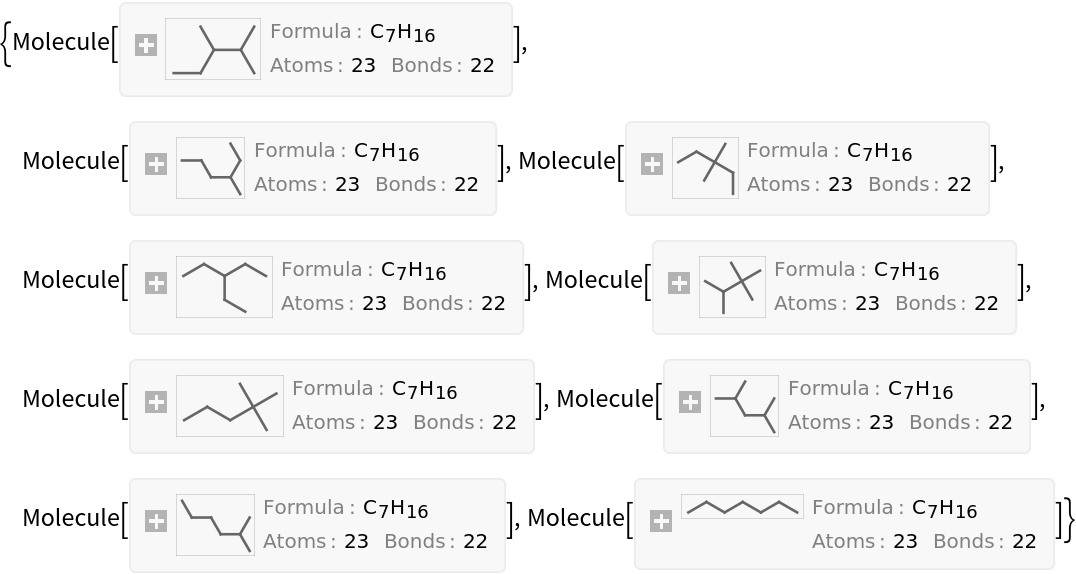

The Balaban index can be interpreted as a measure of the amount of branching within an isomeric set of alkanes. Sort the heptane isomers by their Balaban index:

In[15]:=
SortBy[heptanes, ResourceFunction["BalabanJ"]]
Out[15]=

Properties and Relations (1) 

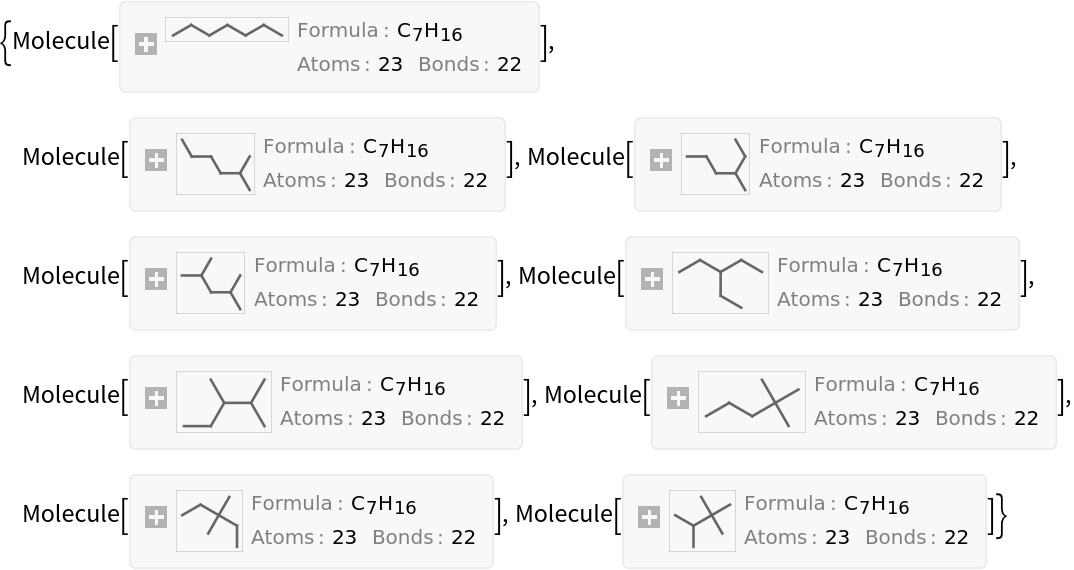The Balaban index of a disconnected graph is 0:

In[16]:=
ResourceFunction["BalabanJ"][\!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{1, 2, 3, 4, 5, 6}, {Null, {{1, 3}, {1, 5}, {2, 4}, {2, 6}, {3, 5}, {4, 6}}}, {GraphLayout -> {"VertexLayout" -> "CircularEmbedding", "PackingLayout" -> None}}]]}, TagBox[GraphicsGroupBox[ GraphicsComplexBox[{{-0.8660254037844389, 0.5000000000000008}, {-0.8660254037844384, -0.4999999999999994}, {3.8285686989269494`*^-16, -1.}, { 0.8660254037844389, -0.5000000000000012}, { 0.8660254037844386, 0.4999999999999993}, { 1.8369701987210297`*^-16, 1.}}, { {Hue[0.6, 0.7, 0.5], Opacity[0.7], {Arrowheads[0.], ArrowBox[{1, 3}, 0.02261146496815286]}, {Arrowheads[0.], ArrowBox[{1, 5}, 0.02261146496815286]}, {Arrowheads[0.], ArrowBox[{2, 4}, 0.02261146496815286]}, {Arrowheads[0.], ArrowBox[{2, 6}, 0.02261146496815286]}, {Arrowheads[0.], ArrowBox[{3, 5}, 0.02261146496815286]}, {Arrowheads[0.], ArrowBox[{4, 6}, 0.02261146496815286]}}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.02261146496815286], DiskBox[2, 0.02261146496815286], DiskBox[3, 0.02261146496815286], DiskBox[4, 0.02261146496815286], DiskBox[5, 0.02261146496815286], DiskBox[6, 0.02261146496815286]}}]], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FrameTicks->None, GridLinesStyle->Directive[ GrayLevel[0.5, 0.4]]]\)]
Out[16]=

Requirements

Wolfram Language 12.3 (May 2021) or above

Version History

  • 1.0.0 – 29 November 2023

Source Metadata

  • Citation:
    • Balaban A.T., "Highly discriminating distance-based topological index." Chemical Physics Letters, vol. 89, no. 5, 399–404, 1982.
      DOI: 10.1016/0009-2614(82)80009-2
    • Knor M., Skrekovski R., Tepeh A., "Mathematical Aspects of Balaban Index." MATCH Communications in Mathematical and in Computer Chemistry, vol. 79, no. 3, 685–716, 2018.
      Available from       https://match.pmf.kg.ac.rs/electronic_versions/Match79/n3/match79n3_685-716.pdf

Related Resources

License Information