Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find an undirected graph whose automorphism group is isomorphic to the given group
ResourceFunction["AutomorphismGraph"][g] finds an undirected graph whose automorphism group is isomorphic to the group g. |
Specify a group:
| In[1]:= |
| Out[1]= |
Construct the graph provided whose automorphism group is isomorphic to our group:
| In[2]:= |
| Out[2]= | 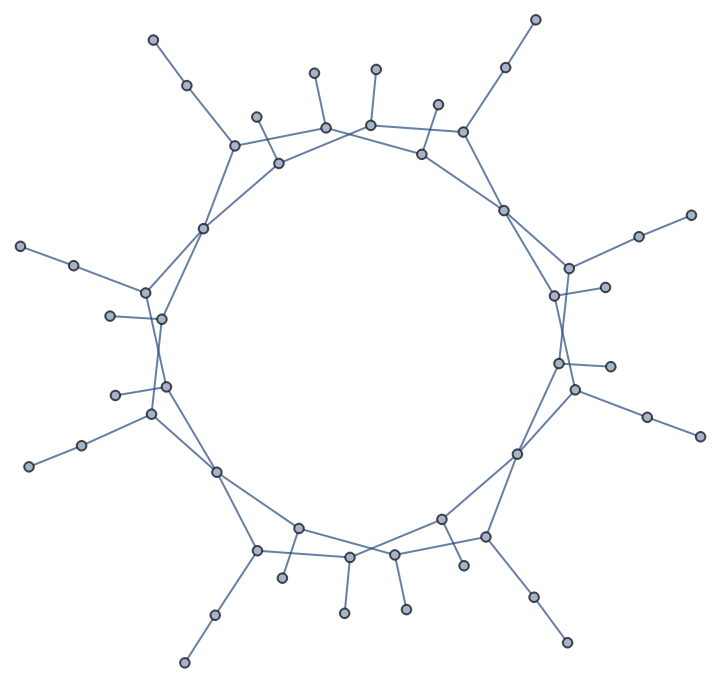 |
Find the graph's automorphism group:
| In[3]:= |
| Out[3]= |  |
Verify that an isomorphism exists between the two groups:
| In[4]:= |
| Out[4]= |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License