Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AugmentedMatrix

Source Notebook

Get the augmented matrix of the system of linear equations

Contributed by: Dennis M Schneider

ResourceFunction["AugmentedMatrix"][eqns,vars]

returns the augmented matrix of the system of equations eqns in the variables vars.

Details and Options

Matrix equations or a list of matrix equations are allowed.
If eqns is a list of expressions, then it is assumed that the right-hand sides are 0.

Examples

Basic Examples (4) 

Find the augmented matrix of a symbolic linear system:

In[1]:=
ResourceFunction[ "AugmentedMatrix"][{Subscript[a, 11] Subscript[x, 1] + Subscript[a, 12] Subscript[x, 2] == Subscript[b, 1], Subscript[a, 21] Subscript[x, 1] + Subscript[a, 22] Subscript[x, 2] == Subscript[b, 2]}, {Subscript[ x, 1], Subscript[x, 2]}] // MatrixForm
Out[1]=

Matrix equations are allowed:

In[2]:=
ResourceFunction["AugmentedMatrix"][( { {1, 6}, {1, 1} } ) . ( { {x}, {y} } ) == ( { {3}, {3} } ), {x, y}] // MatrixForm
Out[2]=

When given a list of expressions, AugmentedMatrix assumes that the right-hand sides are 0:

In[3]:=
ResourceFunction[ "AugmentedMatrix"][{2 (x + y) + z - 5, x + 2 y - z - 6}, {x, y, z}] // MatrixForm
Out[3]=

A mixture of expressions and equations is allowed:

In[4]:=
ResourceFunction[ "AugmentedMatrix"][{2 (x + y) + z - 5, x + 2 y - z - 6 == 3 x + \[Pi]}, {x, y, z}] // MatrixForm
Out[4]=

Applications (5) 

Find all 2×2 matrices whose eigenvectors are (1,2) and (2,-3) :

In[5]:=
matA = Array[a, {2, 2}]; (amat = ResourceFunction[ "AugmentedMatrix"][{matA . {1, 2} == Subscript[\[Lambda], 1] {1, 2}, matA . {2, -3} == Subscript[\[Lambda], 2] {2, -3}}, Flatten[matA]]) // MatrixForm
Out[6]=

Solve the system:

In[7]:=
(ramat = RowReduce[amat]) // MatrixForm
Out[7]=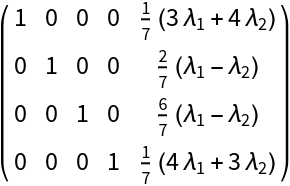

The resulting matrix is:

In[8]:=
(matA = Partition[ramat[[All, -1]], 2] // Simplify) // MatrixForm
Out[8]=

Check that the result satisfies the appropriate eigensystem equation:

In[9]:=
matA . Transpose[{{1, 2}, {2, -3}}] - Transpose[{Subscript[\[Lambda], 1] {1, 2}, Subscript[\[Lambda], 2] {2, -3}}] // Expand
Out[9]=

Another check that the eigenvectors are as stated (up to scale):

In[10]:=
Eigensystem[matA]
Out[10]=

Publisher

Dennis M Schneider

Version History

  • 1.0.0 – 06 August 2019

License Information