Basic Examples (4)
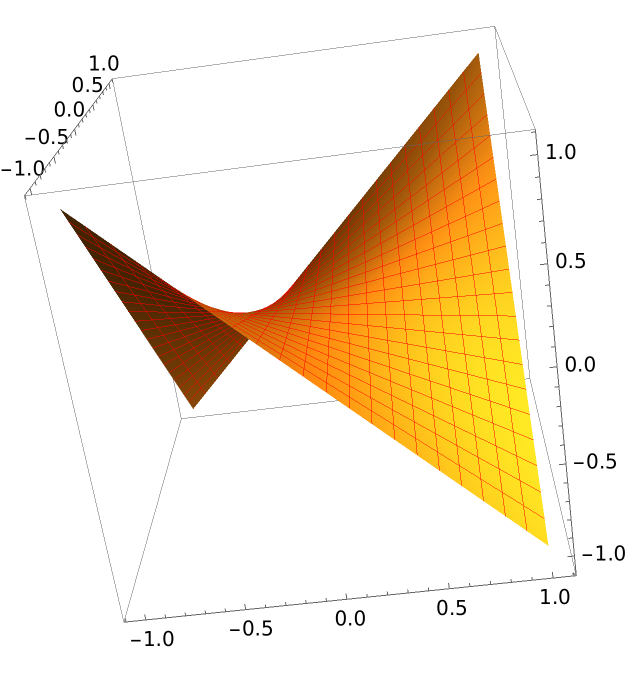
Define a hyperbolic paraboloid:
The asymptotic curves are just straight lines:
The mesh itself represents the asymptotic curves:
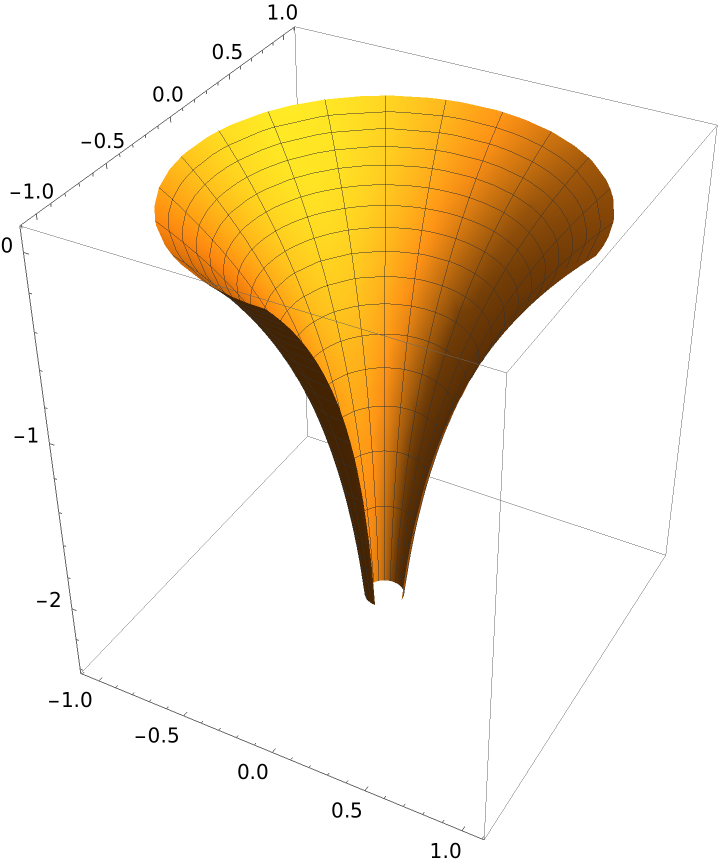
Define a funnel:
Plot it:
Get the equations for asymptotic curves:
Solve the equations:
Solve for variables:
Redefine the funnel parameterization in terms of r=ep-q and θ=p+q:
Plot the asymptotic curves computed in terms of the new coordinates:
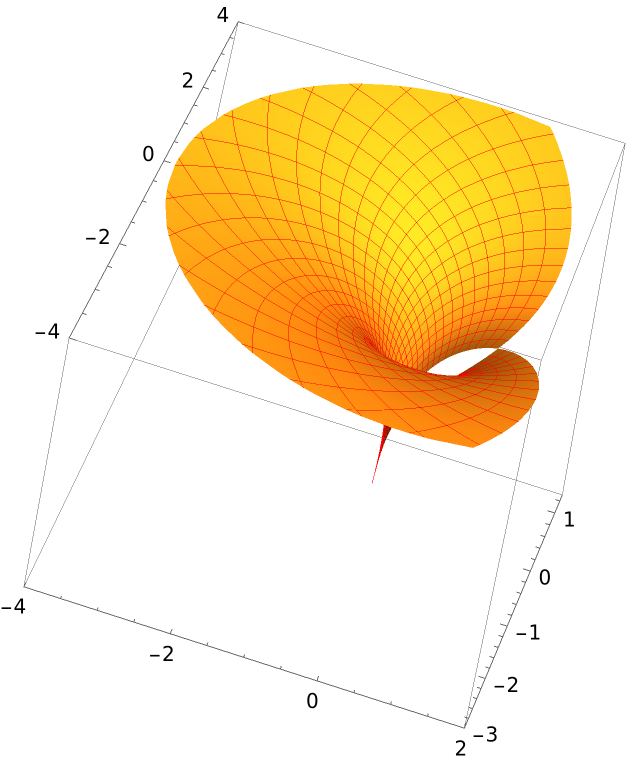
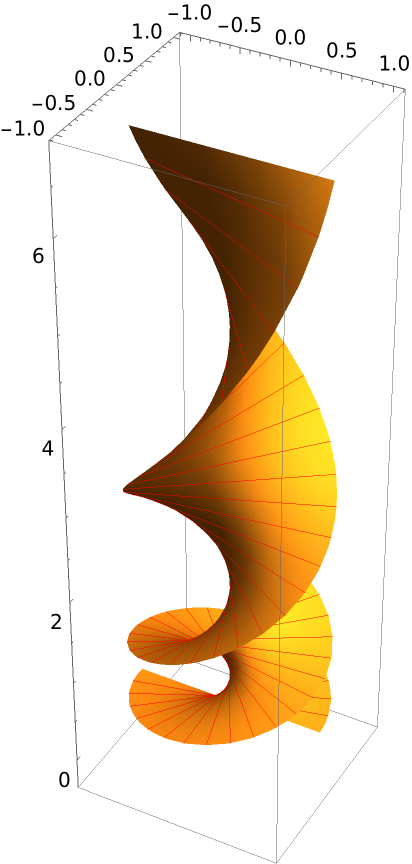
Define the exponentially twisted helicoid:
Plot the surface:
The asymptotic curve equations:
The asymptotic curve solutions:
Solve for parameters:
Redefine the parameterization in terms of r =ec(p-q) and θ=p:
Plot the asymptotic curves on the exponentially twisted helicoid:
Superimpose both the surface and its asymptotic curves:
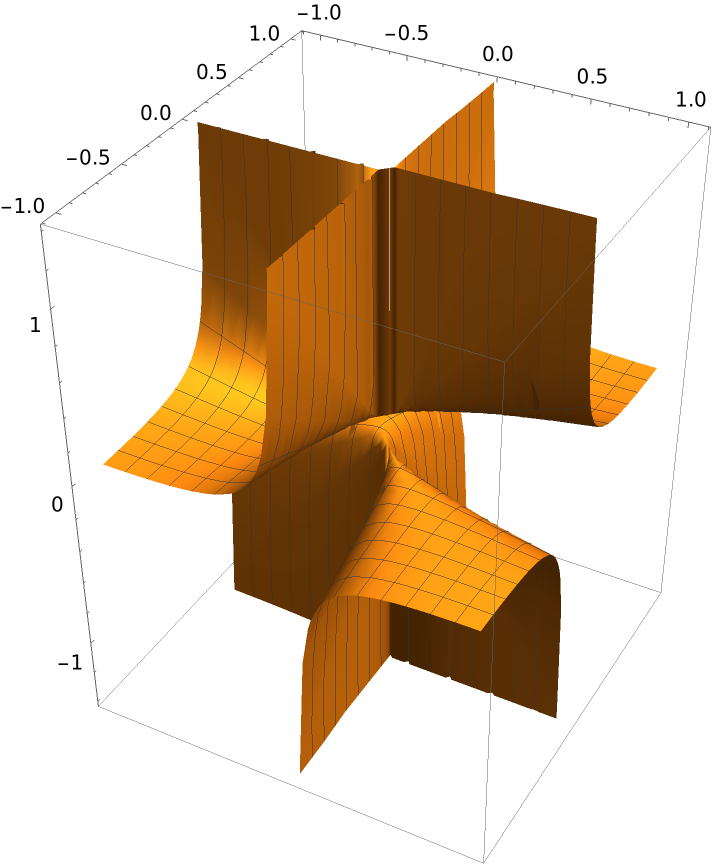
Define a wrinkled surface:
Plot the surface:
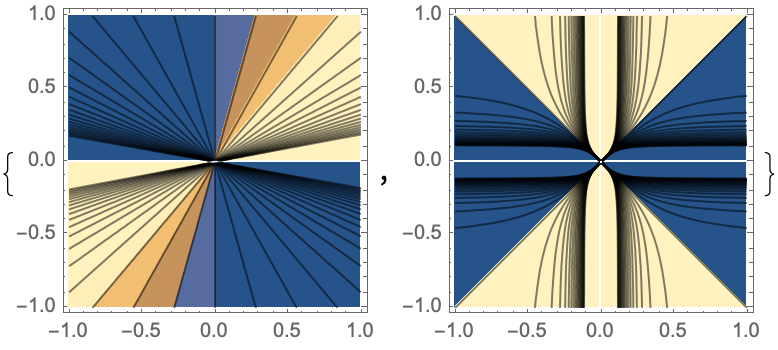
Get the equations for asymptotic curves:
Solve the equations:
Solve for variables:
A way to visualize the curves using ContourPlot:
Properties and Relations (7)
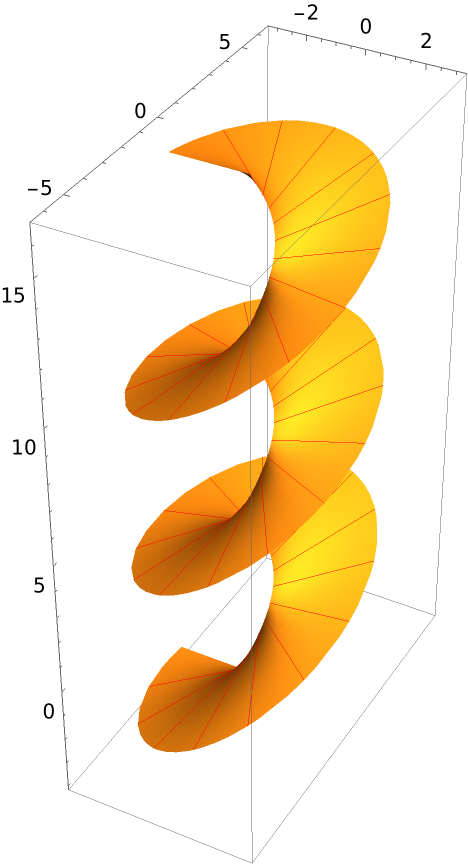
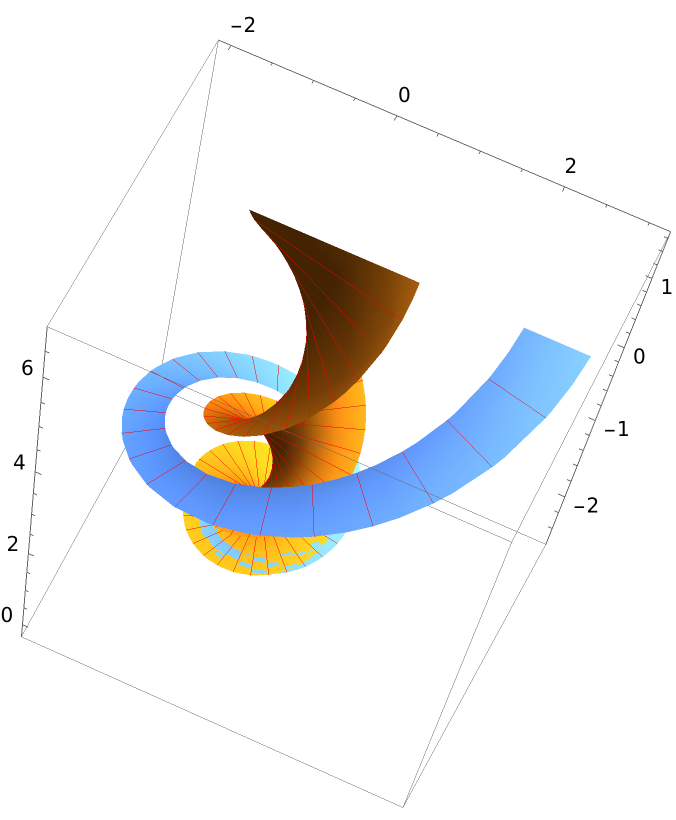
Define an elliptic helicoid:
The inner and outer edges of the elliptical helicoid are helices:
Get the asymptotic curve equation:
For the coefficients of the second fundamental form, only the middle one, f, is nonzero:
Now, verify an instance of the Beltrami-Enneper theorem, starting with the Gaussian curvature:
Take a helix that is contained in the helicoid:
Subtract the square of the torsion to give the same expression as shown previously, verifying the identity:
![exptwistasym[a_, c_][p_, q_] := a {Exp[1/2 c (p - q)] Cos[p], Exp[1/2 c (p - q)] Sin[p], Exp[c p]}](https://www.wolframcloud.com/obj/resourcesystem/images/dd1/dd1022e3-5e5a-45de-82f8-779e0eddca4c/4ce207c2492c8b50.png)

![eqs = Equal @@@ Flatten[{DSolve[Derivative[1][u][v] == u[v]^3/v^3, u[v], v] /. C[1] -> q,
DSolve[Derivative[1][u][v] == u[v]/v, u[v], v] /. C[1] -> p} /. u[v] -> u] // PowerExpand](https://www.wolframcloud.com/obj/resourcesystem/images/dd1/dd1022e3-5e5a-45de-82f8-779e0eddca4c/211b5e22d58b4222.png)
![he = helicoid[1, 2, 1];
ParametricPlot3D[he[u, v], {u, -\[Pi], 5 \[Pi]}, {v, 1/3, 3},
PlotPoints -> {80, 10}, Mesh -> {40, 0}, MeshStyle -> Red]](https://www.wolframcloud.com/obj/resourcesystem/images/dd1/dd1022e3-5e5a-45de-82f8-779e0eddca4c/3f718c34caf6b833.png)