Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AssociationOuter

Source Notebook

Compute the generalized outer product of lists and get an association keyed by arguments

Contributed by: Richard Hennigan (Wolfram Research)

ResourceFunction["AssociationOuter"][f,list1,list2,…]

gives the generalized outer product of the listi as a nested association, forming all possible combinations of the lowest-level elements in each of them as keys, and feeding them as arguments to f for values.

ResourceFunction["AssociationOuter"][f,list1,list2,…,n]

treats as separate elements only sublists at level n in the listi.

ResourceFunction["AssociationOuter"][f,list1,list2,…,n1,n2,…]

treats as separate elements only sublists at level ni in the corresponding listi.

Details

ResourceFunction["AssociationOuter"][f,list1,list2,…] computes all the same f[…] as Outer[f,list1,list2,…]
ResourceFunction["AssociationOuter"][Times,list1,list2] gives an outer product.
Unlike Outer, the heads of all listi must be List.
The listi need not necessarily be cuboidal arrays.
The specifications ni of levels must be positive integers, or Infinity.
If only a single level specification is given, it is assumed to apply to all the listi. If there are several ni, but fewer than the number of listi, the lowest-level elements in the remaining listi will be used.
ResourceFunction["AssociationOuter"] can be used on SparseArray objects, returning a SparseArray object when possible.
ResourceFunction["AssociationOuter"][f,list] is effectively equivalent to AssociationMap[f,list].

Examples

Basic Examples (2) 

Compute an outer product:

In[1]:=
ResourceFunction["AssociationOuter"][f, {a, b}, {x, y, z}]
Out[1]=

Compare to Outer:

In[2]:=
Outer[f, {a, b}, {x, y, z}]
Out[2]=

Outer product of vectors:

In[3]:=
ResourceFunction["AssociationOuter"][Times, {1, 2, 3, 4}, {a, b, c}]
Out[3]=

Outer product of matrices:

In[4]:=
ResourceFunction[ "AssociationOuter"][Times, {{1, 2}, {3, 4}}, {{a, b}, {c, d}}]
Out[4]=

Scope (4) 

The keys are nested so that values can be retrieved in argument order:

In[5]:=
as = ResourceFunction["AssociationOuter"][ f, {a, b}, {x, y, z}, {u, v}]
Out[5]=
In[6]:=
as[a, y, u]
Out[6]=
In[7]:=
as[b, x, v]
Out[7]=

Treat nested lists as rank-1 vectors of sublists:

In[8]:=
ResourceFunction[ "AssociationOuter"][f, {{1, 2}, {3, 4}}, {{a, b}, {c, d}}, 1]
Out[8]=

Arrays can be ragged:

In[9]:=
ResourceFunction[ "AssociationOuter"][Times, {{1, 2}, {3, 4}}, {{a, b, c}, {d, e}}]
Out[9]=

Outer product of SparseArray objects:

In[10]:=
s1 = SparseArray[Table[2^i -> i, {i, 3}]]; s2 = SparseArray[{1} -> 1, {4}];
In[11]:=
ResourceFunction["AssociationOuter"][Times, s1, s2]
Out[11]=

Applications (4) 

Word combinations:

In[12]:=
ResourceFunction[ "AssociationOuter"][StringJoin, {"", "re", "un"}, {"cover", "draw", "wind"}, {"", "ing", "s"}]
Out[12]=

Function combinations:

In[13]:=
fm = ResourceFunction["AssociationOuter"][ Composition, {Sin, Cos, Exp}, {ArcSin, ArcCos, Log}]
Out[13]=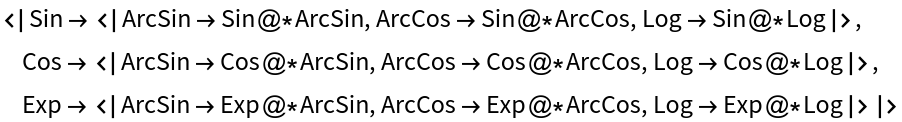
In[14]:=
GraphicsGrid@ Map[Function[f, Plot3D[Re[f[x + I y]], {x, -2, 2}, {y, -2, 2}, Mesh -> None]], Map[Values, fm, {0, 1}], {2}]
Out[14]=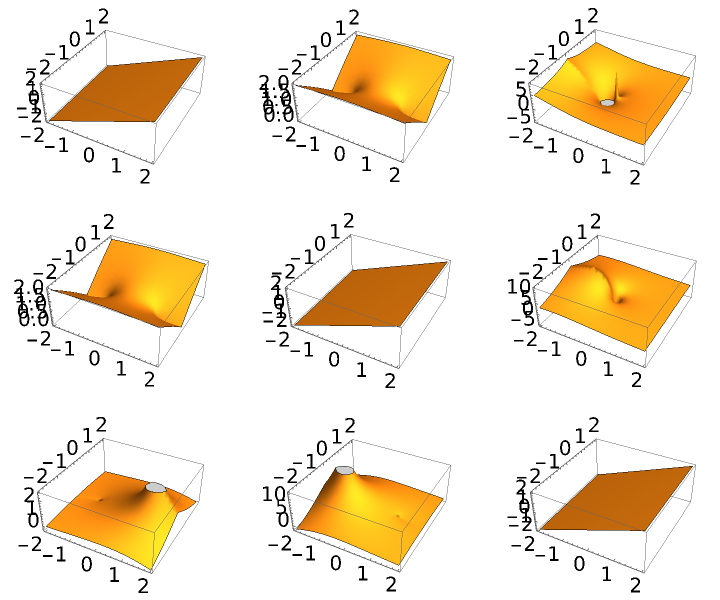

Complete bipartite graph:

In[15]:=
Graphics[Values[ ResourceFunction["AssociationKeyFlatten"][ ResourceFunction["AssociationOuter"][Line[ {##}] &, Table[{x, 1}, {x, 4}], Table[{x, 2}, {x, 4}], 1]]]]
Out[15]=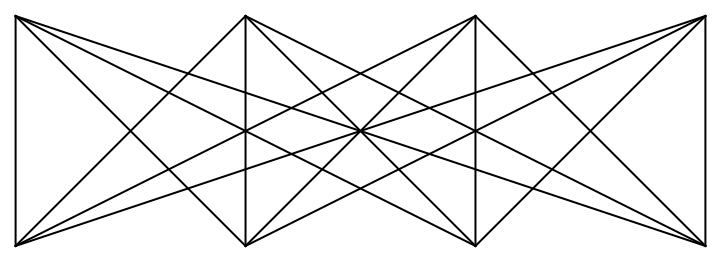

Generate all possible binary trees with nodes from f and leaves from e to depth n:

In[16]:=
trees[f_, e_, 1] = e; trees[f_, e_, n_] := Flatten[Table[ ResourceFunction["AssociationOuter"][#, trees[f, e, r], trees[f, e, n - r]], {r, n - 1}] & /@ f]
In[17]:=
trees[{f}, {a, b}, 3]
Out[17]=

Properties & Relations (6) 

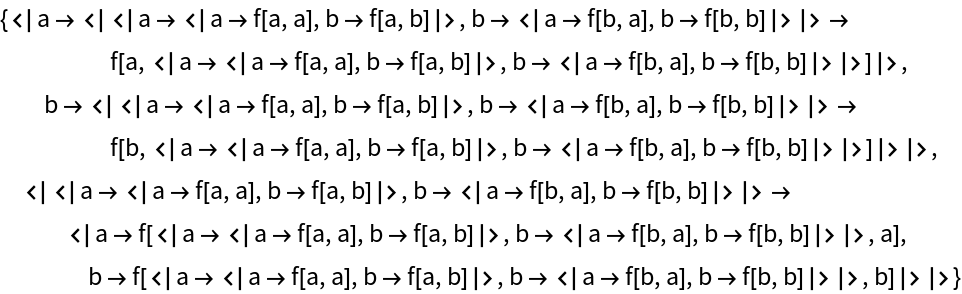If each of the listi are duplicate-free, dimensions of the result are a concatenation of the dimensions of the inputs:

In[18]:=
ResourceFunction["AssociationOuter"][f, {a, b, c}, {1, 2, 3, 4}]
Out[18]=
In[19]:=
Dimensions[%]
Out[19]=

If there are duplicates, the dimensions will correspond to the number of unique elements in each listi:

In[20]:=
ResourceFunction["AssociationOuter"][f, {a, a, a}, {1, 2, 2, 3}]
Out[20]=
In[21]:=
Dimensions[%]
Out[21]=

Compare to Outer, which is unaffected by duplicates:

In[22]:=
Outer[f, {a, a, a}, {1, 2, 2, 3}]
Out[22]=
In[23]:=
Dimensions[%]
Out[23]=

Use Map and Values to convert the result into the format given by Outer:

In[24]:=
ResourceFunction["AssociationOuter"][f, {a, b}, {x, y, z}]
Out[24]=
In[25]:=
Map[Values, %, {0, 1}]
Out[25]=
In[26]:=
Outer[f, {a, b}, {x, y, z}]
Out[26]=

AssociationKeyFlatten can be used to convert the result into a flat association:

In[27]:=
as = ResourceFunction["AssociationOuter"][f, {a, b}, {x, y, z}]
Out[27]=
In[28]:=
flat = ResourceFunction["AssociationKeyFlatten"][as]
Out[28]=

Restore the nested structure with AssociationKeyDeflatten:

In[29]:=
ResourceFunction["AssociationKeyDeflatten"][flat]
Out[29]=

Distribute forms the same combinations of all elements, but in a flat structure:

In[30]:=
Distribute[{{a, b, c}, {x, y}}, List]
Out[30]=
In[31]:=
ResourceFunction["AssociationOuter"][List, {a, b, c}, {x, y}]
Out[31]=

Use AssociationKeyFlatten and Values to get the same result:

In[32]:=
Values[ResourceFunction["AssociationKeyFlatten"][%]]
Out[32]=

AssociationOuter relates to Outer much like AssociationMap relates to Map:

In[33]:=
ResourceFunction["AssociationOuter"][f, {1, 2, 3}]
Out[33]=
In[34]:=
Outer[f, {1, 2, 3}]
Out[34]=
In[35]:=
AssociationMap[f, {1, 2, 3}]
Out[35]=
In[36]:=
Map[f, {1, 2, 3}]
Out[36]=

Possible Issues (3) 

Unlike Outer, the head must be List:

In[37]:=
ResourceFunction["AssociationOuter"][g, f[a, b], f[x, y, z]]
Out[37]=
In[38]:=
Outer[g, f[a, b], f[x, y, z]]
Out[38]=

Unlike Outer, at least two arguments are required:

In[39]:=
ResourceFunction["AssociationOuter"][f]
Out[39]=
In[40]:=
Outer[f]
Out[40]=

Values are nested by arguments in the order they were given to f, even if f is Orderless:

In[41]:=
as = ResourceFunction["AssociationOuter"][Plus, {1, 2, 3}, {4, 5}]
Out[41]=
In[42]:=
as[4, 1]
Out[42]=
In[43]:=
as[1, 4]
Out[43]=

Version History

  • 1.0.0 – 20 December 2021

Related Resources

License Information