Details and Options
The nodes can take the following forms:
| {node1,…} | list of AssessmentFunction objects, comparator functions and/or other ResourceFunction["AssessmentTree"] expressions |
| <|"lbl1"→node1,…|> | Association with keys being node labels and values being AssessmentFunction, comparator function
or other ResourceFunction["AssessmentTree"] expressions |
| node | a single AssessmentFunction, comparator function or another ResourceFunction["AssessmentTree"] |
path should take the form of an
Association <|"origin"→<|True→"destination1",False→"destination2"|>,…|>. Assessment of the answer occurs at each node along the path. The correctness of an answer at
"origin" determines whether the next
node will be
"destination1" or
"destination2".
"origin",
"destination1" and
"destination2" must match the
nodelabels in
nodes.
If the nodes are provided as a list, default nodelabels of "Node1", "Node2"… will be applied. These labels should be used for path in this case.
ResourceFunction["AssessmentTree"][
assess] is a quick way to create an automatic
ResourceFunction["AssessmentTree"] for the case where
assess is an
AssessmentFunction with a mathematical comparison method. It appends an end node to
path which returns an explanation if the answer is mathematically equivalent to the correct answer, but has not been provided in the required form.
If any identifier is not present in the path, that node will be treated as a terminating node.
The following option values can be provided for the ResourceFunction["AssessmentTree"]:
| "ScoreCombiner" | Total | function to combine node "Score" values |
| "AnswerCorrectCombiner" | Apply[Or] | function to combine node "AnswerCorrect" values |
ResourceFunction["AssessmentTree"] enables follow-through marking in multi-part assessments. This means that if a student makes an error in an earlier part of a question, they can still earn marks for subsequent parts where they correctly use the incorrect answer from the earlier part, as long as their approach remains correct.
![at = ResourceFunction["AssessmentTree"][
<|
"Node1" -> PrimeQ,
"Node2" -> OddQ
|>,
<|
"Node1" -> <|False -> "Node2", True -> "Node2"|>
|>
]](https://www.wolframcloud.com/obj/resourcesystem/images/72d/72d1103c-3968-48d4-b21e-669ba4a0048a/2d0a57f6dd1731d6.png)

![at = ResourceFunction["AssessmentTree"][
<|
"Outer1" -> ResourceFunction["AssessmentTree"][
<|
"Inner1" -> GreaterThan[5],
"Inner2" -> (Divisible[#, 3] &)
|>,
<|"Inner1" -> <|False -> "Inner2", True -> "Inner2"|>|>
],
"Outer2" -> AssessmentFunction[12]
|>,
<|"Outer1" -> <|True -> "Outer2"|>|>
]](https://www.wolframcloud.com/obj/resourcesystem/images/72d/72d1103c-3968-48d4-b21e-669ba4a0048a/0ba191131dc2eb54.png)

![at = ResourceFunction["AssessmentTree"][
<|
"Node1" -> AssessmentFunction[
(x - 1) (x + 1) -> <|
"Explanation" -> "Well done, you successfully factorized the polynomial."|>,
"PolynomialResult"
],
"Node2" -> AssessmentFunction[
(x - 1) (x + 1) -> <|"Score" -> 0.5, "Explanation" -> StringJoin[
"Your answer is mathematically equivalent to the correct",
" answer, but has not been provided not in the required form."
]|>,
"CalculusResult"
]
|>,
<|
"Node1" -> <|False -> "Node2"|>
|>
]](https://www.wolframcloud.com/obj/resourcesystem/images/72d/72d1103c-3968-48d4-b21e-669ba4a0048a/28450527dd1436a1.png)

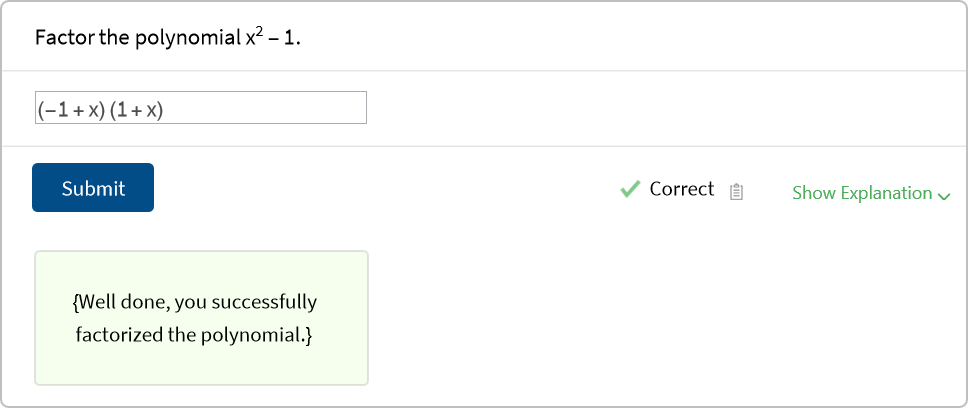
![at = ResourceFunction["AssessmentTree"][
AssessmentFunction[
(x - 1) (x + 1) -> <|
"Explanation" -> "Well done, you successfully factorized the polynomial."|>,
"PolynomialResult"
]
]](https://www.wolframcloud.com/obj/resourcesystem/images/72d/72d1103c-3968-48d4-b21e-669ba4a0048a/1fedba6b9efd5936.png)


![ResourceFunction["AssessmentTree"][
<|
"Node1" -> (True &), (* Always award 1 point *)
"Node2" -> (True &), (* Always award 1 point *)
"Node3" -> (False &) (* Always award 0 points *)
|>,
<|"Node1" -> <|True -> "Node2"|>, "Node2" -> <|True -> "Node3"|>|>
][x]["Score"]](https://www.wolframcloud.com/obj/resourcesystem/images/72d/72d1103c-3968-48d4-b21e-669ba4a0048a/739f2f80da3c9ef8.png)
![ResourceFunction["AssessmentTree"][
<|
"Node1" -> (True &), (* Always award 1 point *)
"Node2" -> (True &), (* Always award 1 point *)
"Node3" -> (False &) (* Always award 0 points *)
|>,
<|"Node1" -> <|True -> "Node2"|>, "Node2" -> <|True -> "Node3"|>|>,
"ScoreCombiner" -> Mean
][x]["Score"]](https://www.wolframcloud.com/obj/resourcesystem/images/72d/72d1103c-3968-48d4-b21e-669ba4a0048a/578f19ed58cd759c.png)
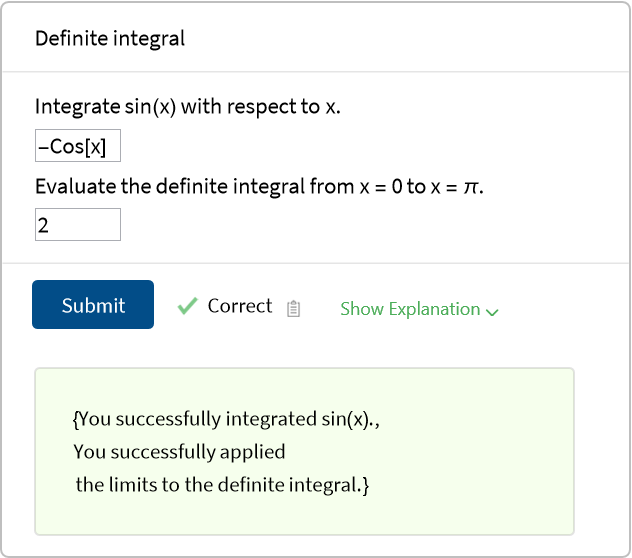
![at = ResourceFunction["AssessmentTree"][
<|
"Indefinite" -> (AssessmentFunction[
(-Cos[x] + C[1]) -> <|
"Score" -> 1,
"Explanation" -> "You successfully integrated sin(x)."
|>,
"CalculusResult"
][
#[[1]] (* 1st answer *)
] &),
"Definite" -> (AssessmentFunction[
(* Answer key defined as a function of the 1st answer *)
((#[[1]] /. x -> \[Pi]) - (#[[1]] /. x -> 0)) -> <|
"Score" -> 1, "Explanation" -> "You successfully applied the limits to the definite integral."
|>
][
#[[2]] (* 2nd answer *)
] &)
|>,
<|
(* Both branches of the tree are the same *)
"Indefinite" -> <|True -> "Definite", False -> "Definite"|>
|>,
"AnswerCorrectCombiner" -> Apply[And]
]](https://www.wolframcloud.com/obj/resourcesystem/images/72d/72d1103c-3968-48d4-b21e-669ba4a0048a/1c665ba5a8c4a8cb.png)

![QuestionObject[
QuestionInterface["TextCompletion", <|
"Prompt" -> "Definite integral",
"Template" -> "Integrate sin(x) with respect to x.
``
Evaluate the definite integral from x = 0 to x = \[Pi].
``"
|>],
at[Interpreter["MathExpression"][#]] &
]](https://www.wolframcloud.com/obj/resourcesystem/images/72d/72d1103c-3968-48d4-b21e-669ba4a0048a/531f29728ca042d9.png)

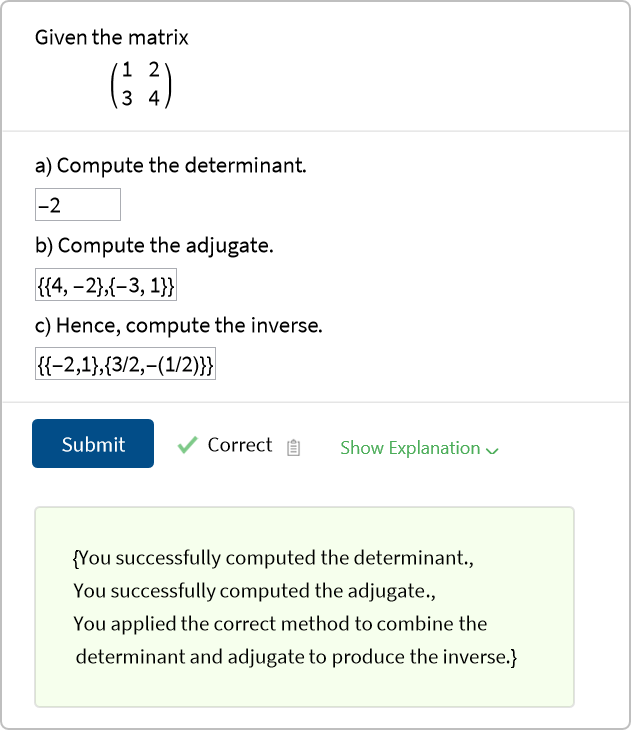
![]() a) Compute the determinant.
b) Compute the adjugate.
c) Hence, compute the inverse.
a) Compute the determinant.
b) Compute the adjugate.
c) Hence, compute the inverse.![at = With[{mat = {{1, 2}, {3, 4}}},
ResourceFunction["AssessmentTree"][
<|
"Determinant" -> (AssessmentFunction[
Det[mat] -> <|
"Score" -> 1, "Explanation" -> "You successfully computed the determinant."
|>
][#[[1]] (* 1st answer *)] &),
"Adjugate" -> (AssessmentFunction[
Adjugate[mat] -> <|
"Score" -> 1, "Explanation" -> "You successfully computed the adjugate."
|>
][#[[2]] (* 2nd answer *)] &),
"Inverse" -> (AssessmentFunction[
(* Answer key defined as a function of the 1st and 2nd answers *)
(#[[2]] / #[[1]]) -> <|
"Score" -> 1, "Explanation" -> "You applied the correct method to combine the determinant and adjugate to produce the inverse."
|>
][#[[3]] (* 3rd answer *)] &)
|>,
<|
(* Both branches of the tree are the same *)
"Determinant" -> <|True -> "Adjugate", False -> "Adjugate"|>,
"Adjugate" -> <|True -> "Inverse", False -> "Inverse"|>
|>
]
]](https://www.wolframcloud.com/obj/resourcesystem/images/72d/72d1103c-3968-48d4-b21e-669ba4a0048a/32c9fa57c7d82d00.png)

![QuestionObject[
QuestionInterface["TextCompletion", <|
"Prompt" -> "Given the matrix
\!\(\*TagBox[\((\[NoBreak]\*GridBox[{
{1, 2},
{3, 4}
},\nGridBoxAlignment->{\"Columns\" -> {{Center}}, \"Rows\" -> {{Baseline}}},\nGridBoxSpacings->{\"Columns\" -> {\nOffset[0.27999999999999997`], {\nOffset[0.7]}, \nOffset[0.27999999999999997`]}, \"Rows\" -> {\nOffset[0.2], {\nOffset[0.4]}, \nOffset[0.2]}}]\[NoBreak])\),
Function[BoxForm`e$, \nMatrixForm[BoxForm`e$]]]\)",
"Template" -> "a) Compute the determinant.
``
b) Compute the adjugate.
``
c) Hence, compute the inverse.
``"
|>],
at[Interpreter["MathExpression"][#]] &
]](https://www.wolframcloud.com/obj/resourcesystem/images/72d/72d1103c-3968-48d4-b21e-669ba4a0048a/42c2dc4c10c2919b.png)