Basic Examples (3) 

The only articulation vertex of a star is its center:

In[1]:=

Out[1]=

All vertices of a path, except the end vertices, are articulation vertices:

In[2]:=

Out[2]=

Articulation vertices a random graph:

In[3]:=

Out[3]=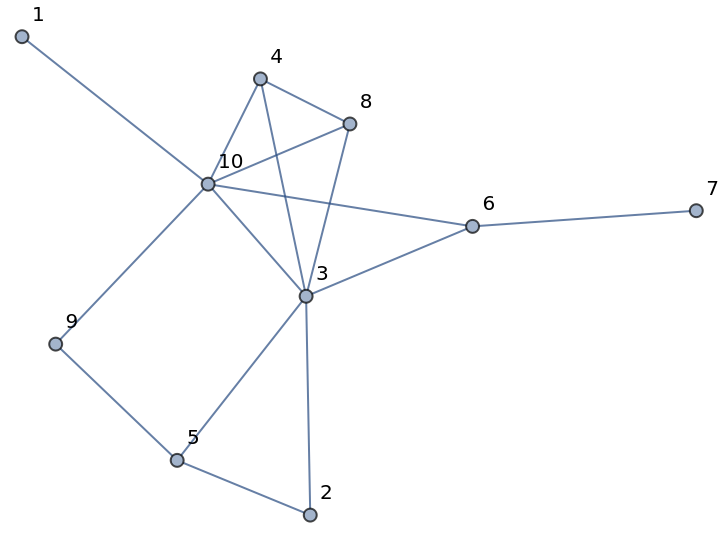

In[4]:=

Out[4]=

In[5]:=

Out[5]=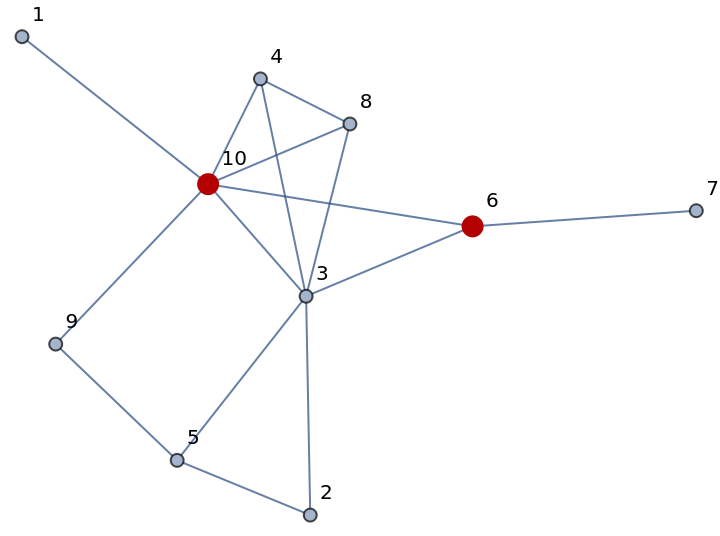

Scope (4) 

ArticulationVertices works on undirected graphs:

In[6]:=

Out[6]=

Directed graphs:

In[7]:=

Out[7]=

Multigraphs:

In[8]:=

Out[8]=

Mixed graphs:

In[9]:=

Out[9]=

Properties and Relations (7) 

Define a graph with multiple articulation vertices:

In[10]:=

In[11]:=

Out[11]=

Deleting any of the articulation vertices, disconnects the graph:

In[12]:=

Out[12]=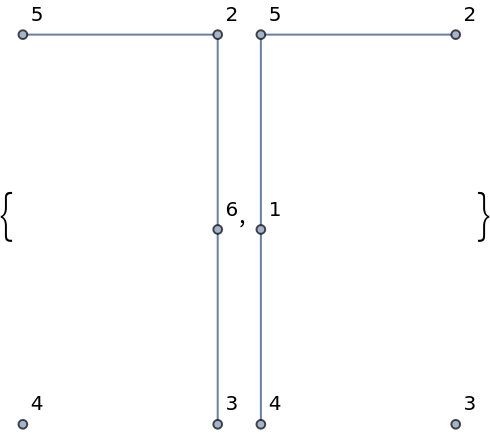

In[13]:=

Out[13]=

FindVertexCut finds a single vertex cut possibly containing multiple vertices:

In[14]:=

In[15]:=

In[16]:=

Out[16]=

For this graph there are no articulation vertices:

In[17]:=

Out[17]=

For graphs with vertex connectivity 1, the cut vertex returned by FindVertexCut is one of the articulation vertices:

In[18]:=

In[19]:=

Out[19]=

In[20]:=

Out[20]=

A graph with no articulation vertices is biconnected:

In[21]:=

In[22]:=

Out[22]=

In[23]:=

Out[23]=

A graph with a vertex of degree 1 cannot be biconnected:

In[24]:=

Out[24]=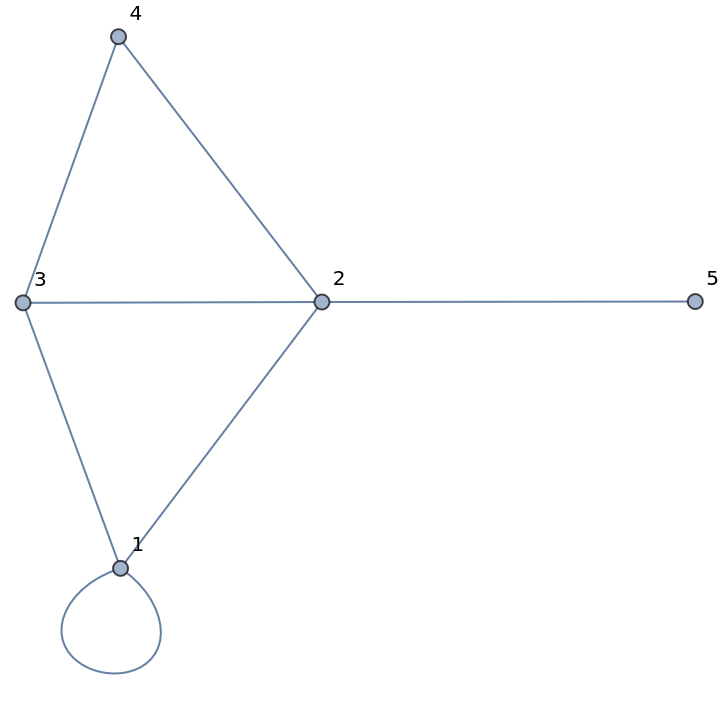

In[25]:=

Out[25]=

An articulation vertex is a member of at least two biconnected components:

In[26]:=

In[27]:=

Out[27]=

In[28]:=

Out[28]=

GraphData[name,{"Graph","ArticulationVertices"}] gives the articulation vertices of a named graph:

In[29]:=

Out[29]=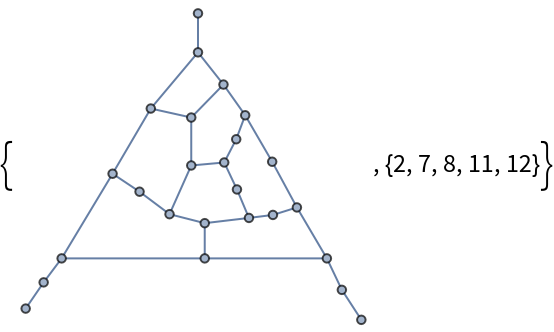

In[30]:=

Out[30]=