Function Repository Resource:

ArrayContractThread

Source Notebook

General contraction of levels of the outer product of arrays

Contributed by: Jose Martin-Garcia

ResourceFunction["ArrayContractThread"][f,{a₁,a₂,…,a_n},{{l₁,l₂,…,l_n}}]

contracts level l₁ of array a₁, level l₂ of array a₂,… in Outer[f,a₁,…,a_n], using head Plus.

ResourceFunction["ArrayContractThread"][f,arrays,{ctr₁,ctr₂,…}]

performs several contractions.

ResourceFunction["ArrayContractThread"][f,arrays,ctrs,g]

performs contractions ctrs using head g.

ResourceFunction["ArrayContractThread"][f,{a₁,…,a_n},ctrs,g,{d₁,…,d_n}]

performs contractions assuming that only the first d_i levels of array a_i are array levels.

Details and Options

Each contraction ctr_k in the contraction list must be a list of non-negative integers {l_k1,…,l_kn}. A positive l_ki indicates the level of array a_i to be contracted during contraction ctr_k . A zero l_ki indicates that array a_i does not participate in contraction ctr_k.

For each contraction ctr_k, all levels l_ki must have the same dimension. That is, Dimensions[a_i][[l_ki]] must coincide for all i for each k.

Each array a_i in ResourceFunction["ArrayContractThread"][f,{a₁,…,a_n},…] must be rectangular up to the deepest level involved in the contractions.

The effective depth d_i in ResourceFunction["ArrayContractThread"][f,{a₁,…,a_n},ctrs,g,{d₁,…,d_n}] can be used to indicate that array a_i should be treated as if it had only d_i levels. Therefore d_i must be an integer between 0 and the depth of a_i, and all contraction levels l_ki must be between 0 and d_i. Following the precedent of Outer, by default d_i is chosen to be the depth of the array a_i.

ResourceFunction["ArrayContractThread"] cannot contract levels of the same array. Use the resource function ArrayContract for that.

Examples

Basic Examples (2)

Take two arrays:

In[1]:=

Out[1]=

In[2]:=

Out[2]=

Contract the first levels of the arrays:

In[3]:=

Out[3]=

Contract level 2 of the first array and level 1 of the second:

In[4]:=

Out[4]=

Take three arrays:

In[5]:=

Out[5]=

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Perform two simultaneous contractions:

In[8]:=

Out[8]=

Use head g for the same contractions:

In[9]:=

Out[9]=

Scope (6)

Use arrays of any depth and dimension:

In[10]:=

a = Array[Subscript[x, ##] &, {2, 3}];
b = Array[Subscript[y, ##] &, {3, 2, 4}];
c = Array[Subscript[z, ##] &, {1, 2, 4, 3}];

In[11]:=

Out[11]=

Perform any number of contractions simultaneously:

In[12]:=

In[13]:=

Out[13]=

In[14]:=

Out[14]=

In[15]:=

Out[15]=

Use any head for contractions:

In[16]:=

In[17]:=

Out[17]=

Specify the effective levels of the arrays:

In[18]:=

In[19]:=

Out[19]=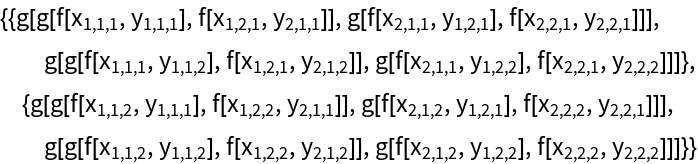

In[20]:=

Out[20]=

In[21]:=

Out[21]=

In[22]:=

Out[22]=

Arrays do not need to be rectangular beyond the contraction levels:

In[23]:=

Out[23]=

In[24]:=

Out[24]=

Effective depths can be zero, and then the whole array is treated as a scalar:

In[25]:=

In[26]:=

Out[26]=

Properties and Relations (8)

Inner is a particular case of ArrayContractThread:

In[27]:=

In[28]:=

Out[28]=

In[29]:=

Out[29]=

In[30]:=

Out[30]=

In[31]:=

Out[31]=

Dot is a particular case of ArrayContractThread:

In[32]:=

a = Array[Subscript[x, ##] &, {2, 2}];
b = Array[Subscript[y, ##] &, {2, 2}];
c = Array[Subscript[z, ##] &, {2, 2}];

In[33]:=

Out[33]=

In[34]:=

Out[34]=

Outer is a particular case of ArrayContractThread:

In[35]:=

In[36]:=

Out[36]=

In[37]:=

Out[37]=

In[38]:=

Out[38]=

ArrayContractThread can handle scalar factors, but Outer cannot:

In[39]:=

Out[39]=

In[40]:=

Out[40]=

MapThread is a particular case of ArrayContractThread:

In[41]:=

In[42]:=

Out[42]=

In[43]:=

Out[43]=

Thread is a particular case of ArrayContractThread:

In[44]:=

In[45]:=

Out[45]=

TensorContract of a TensorProduct expression is a particular case of ArrayContractThread if each contraction involves at most one level of each array:

In[46]:=

In[47]:=

Out[47]=

The special case ArrayContractThread[f,{expr},{{n}},List,n] is equivalent to Map[f,expr,{n}]:

In[48]:=

In[49]:=

Out[49]=

In[50]:=

Out[50]=

In[51]:=

Out[51]=

The special case ArrayContractThread[Identity,{expr},{{n}},g,n] is equivalent to Apply[g,expr,{n-1}]:

In[52]:=

In[53]:=

Out[53]=

In[54]:=

Out[54]=

In[55]:=

Out[55]=

Possible Issues (2)

ArrayContractThread effectively normalizes sparse and structured arrays in input:

In[56]:=

Out[56]=

Compare to the equivalent computation with Outer:

In[57]:=

Out[57]=

In[58]:=

Out[58]=

Publisher

Jose Martin-Garcia

Version History

1.0.0 – 05 August 2020

Related Resources

Author Notes

• This function is rather slow, and normalizes everything. It is essentially a prototype to explore the generality of the possible concept.

• This function could still be generalized as follows: 1) the fourth argument could take a list of heads, one per contraction (this will be implemented in 12.2)—right now all contractions in the third argument use the same head in the fourth argument; and 2) like Tr, it should be possible to contract to the lowest dimension, instead of requiring coinciding dimensions.

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License