Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ArithmeticProgression

Source Notebook

Produce an arithmetic progression with a specified difference

Contributed by: Pedro Cabral

ResourceFunction["ArithmeticProgression"][n,d]

produces an arithmetic progression of n terms starting at d and incrementing by d.

ResourceFunction["ArithmeticProgression"][n,d,a]

produces an arithmetic progression starting term at a rather than d.

Examples

Basic Examples (3) 

Compute the first 10 terms of an arithmetic progression with a common difference of :

In[1]:=
ResourceFunction["ArithmeticProgression"][10, 3/2]
Out[1]=

Perform a ListLinePlot of different arithmetic progressions:

In[2]:=
ListLinePlot[{ResourceFunction["ArithmeticProgression"][10, 2], ResourceFunction["ArithmeticProgression"][10, \[Pi]], ResourceFunction["ArithmeticProgression"][10, \[Pi]^2]}]
Out[2]=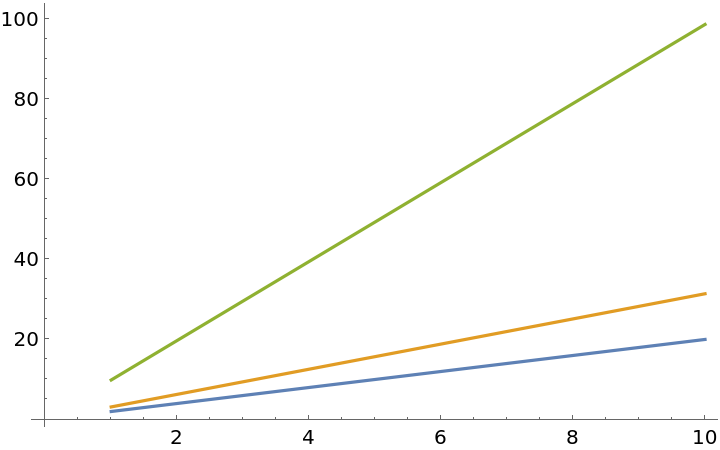

Get 30 terms with a common difference of , starting at 20:

In[3]:=
ResourceFunction["ArithmeticProgression"][30, 5/2, 20]
Out[3]=

Scope (1) 

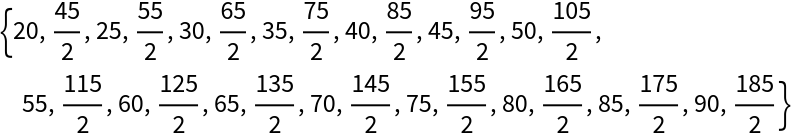ArithmeticProgression can handle complex numbers, symbols and constants:

In[4]:=
ResourceFunction["ArithmeticProgression"][5, \[Theta]^2 + 2 I + \[Pi]]
Out[4]=

Properties and Relations (3) 

An arithmetic progression of common difference 1 is the same as a Range:

In[5]:=
ResourceFunction["ArithmeticProgression"][100, 1] == Range[100]
Out[5]=

The Mean of an arithmetic progression is the same as its Median:

In[6]:=
Mean[ResourceFunction["ArithmeticProgression"][42, 3/2]] == Median[ResourceFunction["ArithmeticProgression"][42, 3/2]]
Out[6]=

The sum of all terms is the half the length of the progression times the first term plus the last term:

In[7]:=
p = ResourceFunction["ArithmeticProgression"][11, 3]
Out[7]=
In[8]:=
Total[p] == Length[p]/2*(First[p] + Last[p])
Out[8]=

Publisher

Pedro Cabral

Version History

  • 1.0.0 – 09 September 2020

Related Resources

License Information