Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Areal

Source Notebook

Given a simplex and point, convert back and forth between areal and Cartesian coordinates

Contributed by: Wolfram Staff

ResourceFunction["Areal"][simplex,point]

converts point between Cartesian and areal coordinates based on simplex.

Details and Options

ResourceFunction["Areal"] coordinates total to one.
A simplex can be considered any of the following:
Point[v]point
Line[{v1,v2}]line segment
Triangle[{v1,v2,v3}] or Polygon[{v1,v2,v3}]filled triangle
Tetrahedron[{v1,v2,v3,v4}]filled tetrahedron
Simplex[{v1,v2,…,vn}]an n-1 dimensional simplex

Examples

Basic Examples (3) 

Vertices of a 3-4-5 triangle give an example of a 2-simplex. We can convert back and forth:

In[1]:=
ResourceFunction["Areal"][{{0, 0}, {3, 0}, {0, 4}}, {1, 2}]
Out[1]=
In[2]:=
ResourceFunction["Areal"][{{0, 0}, {3, 0}, {0, 4}}, {1/6, 1/3, 1/2}]
Out[2]=

Given a line segment or 1-simplex defined by two points some other points on the line can be calculated by areal coordinates:

In[3]:=
line = Table[ ResourceFunction[ "Areal"][{{1, -1, 2}, {3, 1, 4}}, {a, 1 - a}], {a, -2, 2, 4/5}]
Out[3]=

Areal coordinates always have a sum of one:

In[4]:=
ResourceFunction["Areal"][{{1, -1, 2}, {3, 1, 4}}, #] & /@ line
Out[4]=

Scope (3) 

The minimal sign of an areal coordinate determines if a point is inside, outside, or on the boundary of a given simplex:

In[5]:=
triangle = {{1, 7}, {3, 1}, {7, 3}}; inoutor = {Min[Sign[ResourceFunction["Areal"][triangle, #]]], #} & /@ Tuples[Range[7], {2}]; Graphics[{EdgeForm[Black], Yellow, Polygon[triangle], {{Red, Blue, Green}[[#[[1]] + 2]], Disk[#[[2]], .1]} & /@ inoutor}]
Out[7]=

By Pick’s theorem, interior + boundary/2 -1 = area, so this triangle should have area 12+6/2-1 = 14:

In[8]:=
Area[Polygon[triangle]]
Out[8]=

Some graphics primitives that correspond to simplices are also supported:

In[9]:=
ResourceFunction["Areal"][ Tetrahedron[{{0, 0, 0}, {3, 0, 0}, {0, 4, 0}, {0, 0, 5}}], {1, 2, 3}]
Out[9]=

The following are equivalent:

In[10]:=
ResourceFunction["Areal"][Triangle[{{0, 0}, {3, 0}, {0, 4}}], {1, 2}]
Out[10]=
In[11]:=
ResourceFunction["Areal"][Simplex[{{0, 0}, {3, 0}, {0, 4}}], {1, 2}]
Out[11]=
In[12]:=
ResourceFunction["Areal"][Polygon[{{0, 0}, {3, 0}, {0, 4}}], {1, 2}]
Out[12]=

Applications (2) 

The areal coordinates of the incenter are proportional to the sides of the triangle:

In[13]:=
randomtriangle = RandomReal[{-1, 1}, {3, 2}]; sides = EuclideanDistance @@ # & /@ Subsets[Reverse[randomtriangle], {2}]; incenter = Insphere[randomtriangle][[1]]; ResourceFunction["Areal"][randomtriangle, incenter]/ sides
Out[14]=

The trilinear coordinate formula of a triangle center can be used with areal coordinates to generate that center; here is a calculation of the orthocenter, where the altitudes of the triangle intersect:

In[15]:=
triangle = {{1, 7}, {3, 1}, {7, 3}}; sides = EuclideanDistance @@ # & /@ Subsets[Reverse[triangle], {2}]; orthocenterformula = (-a^4 + (b^2 - c^2)^2); baryortho = Table[orthocenterformula /. Thread[{a, b, c} -> RotateLeft[sides, n]], {n, 0, 2}]; ortho = N[ ResourceFunction["Areal"][triangle, baryortho/Total[baryortho]]]; Graphics[{EdgeForm[Black], Yellow, Polygon[triangle], Green, Disk[ortho, .1], Black, InfiniteLine[{ortho, #}] & /@ triangle}]
Out[20]=

Properties and Relations (2) 

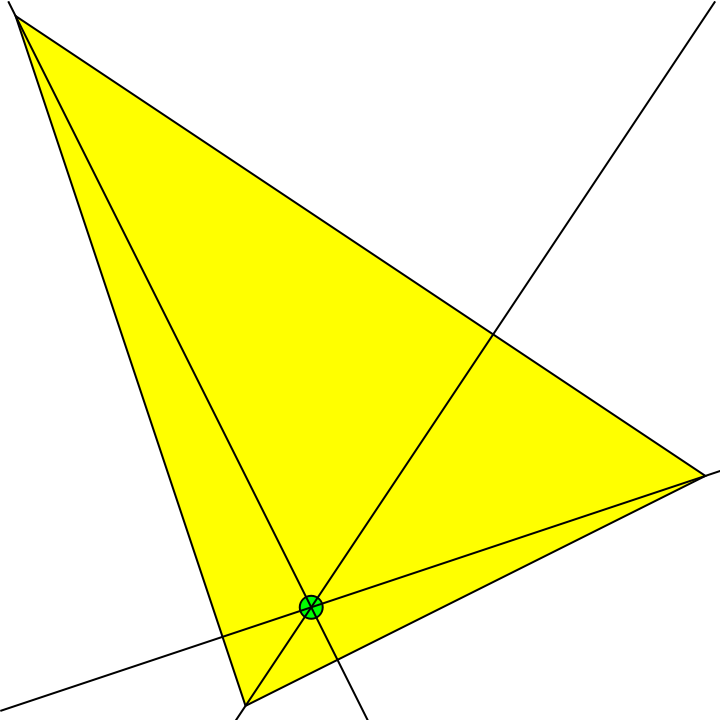A tetrahedron is an example of a 3-simplex. We can convert back and forth:

In[21]:=
ResourceFunction[ "Areal"][{{0, 0, 0}, {3, 0, 0}, {0, 4, 0}, {0, 0, 5}}, {1, 2, 3}]
Out[21]=
In[22]:=
ResourceFunction[ "Areal"][{{0, 0, 0}, {3, 0, 0}, {0, 4, 0}, {0, 0, 5}}, {-(13/30), 1/ 3, 1/2, 3/5}]
Out[22]=

The areal coordinates correspond to the area/volume when the Cartesian point is substituted for a point of the simplex and divided by the original volume; if the point is outside of the simplex a negative value is returned:

In[23]:=
Volume[Simplex[{{1, 2, 3}, {3, 0, 0}, {0, 4, 0}, {0, 0, 5}}]]/ Volume[Simplex[{{0, 0, 0}, {3, 0, 0}, {0, 4, 0}, {0, 0, 5}}]]
Out[23]=

Possible Issues (1) 

The plane perpendicular to vector (1/3, 1/3, 1/3) has all totals equal to 1, so points on this plane are assumed to be areal coordinates and get converted to Cartesian coordinates. There exists a triangle where the areal and Cartesian coordinates are the same, but in general there is no back function for this special case:

In[24]:=
Manipulate[ Graphics3D[{Point /@ tricky, Line[{#, ResourceFunction["Areal"][ Table[RotateRight[tricky[[k]], n], {n, 0, 2}], #]}] & /@ tricky}, ViewPoint -> {3, 3, 3}, Boxed -> False], {k, 1, Length[tricky], 1}, Initialization :> (tricky = SortBy[Flatten[ Permutations[Append[#, 1 - Total[#]]] & /@ Subsets[FareySequence[4], {2}], 1], {Max[Denominator[#]], Reverse[#]} &];)]
Out[24]=

Neat Examples (2) 

Arrange 25 trees in 18 lines of 5 trees:

In[25]:=
triangle = {{Sqrt[3], -1}, {0, 2}, {-Sqrt[3], -1}}; base = {{0, 0, 1}, {0, 1, 1}, {1, 1, 1}, {0, 1, 2}, {1, 1, 2}, {1, 2, 2}, {1, 2, 3}}; coords = Flatten[Permutations /@ base, 1]; lines = Union[Flatten[#, 1]] & /@ Select[GatherBy[Subsets[coords, {2}], RowReduce], Length[#] == 10 &]; Graphics[{ Cyan, Line[ ResourceFunction["Areal"][triangle, #/Total[#]] & /@ #] & /@ lines, Black, Text[Row[#], ResourceFunction["Areal"][triangle, #/Total[#]]] & /@ coords}]
Out[26]=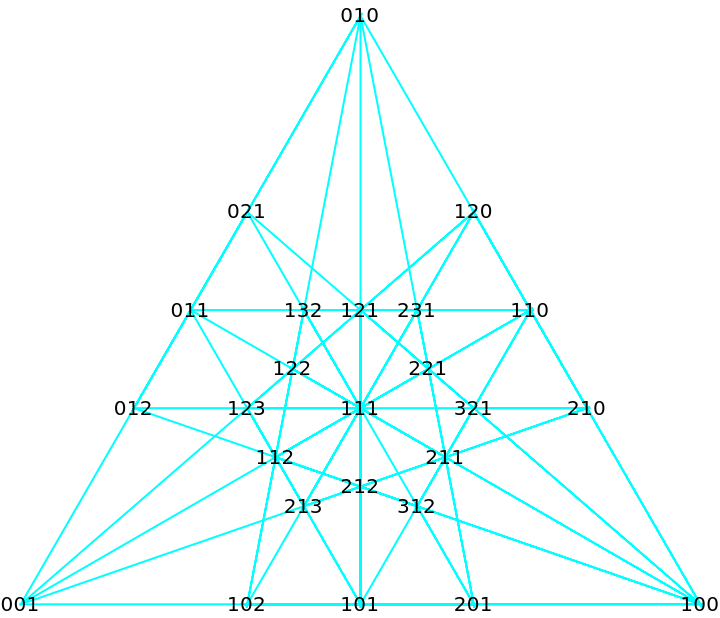

Arrange 149 points in 241 lines of 5:

In[27]:=
tetra = {{-1, -1, -1}, {1, 1, -1}, {1, -1, 1}, {-1, 1, 1}}; base = {{0, 0, 0, 1}, {0, 0, 1, 1}, {0, 1, 1, 1}, {1, 1, 1, 1}, {0, 0, 1, 2}, {0, 1, 1, 2}, {0, 1, 2, 2}, {1, 1, 1, 2}, {1, 1, 2, 2}, {1, 2, 2, 2}, {0, 1, 2, 3}, {1, 1, 2, 3}, {1, 2, 2, 3}, {1, 2, 3, 3}, {2, 3, 4, 5}}; coords = Flatten[Permutations /@ base, 1]; lines = Union[Flatten[#, 1]] & /@ Select[GatherBy[Subsets[coords, {2}], RowReduce], Length[#] == 10 &]; Graphics3D[ Tube[ResourceFunction["Areal"][tetra, #/Total[#]] & /@ #] & /@ lines, Boxed -> False, SphericalRegion -> True]
Out[28]=

Requirements

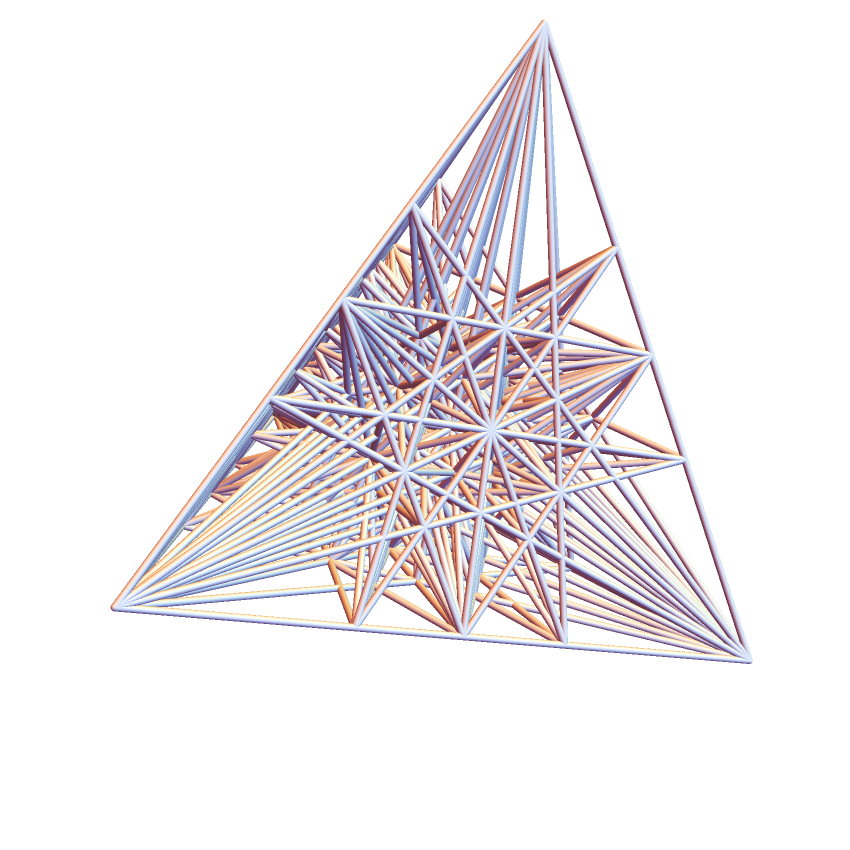Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 13 February 2019

Related Resources

License Information