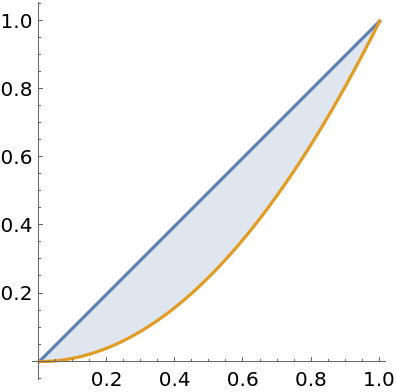
Basic Examples (1)
Find the area between two curves:
Scope (4)
Find the area of the region enclosed by two curves:
Where the curves do not meet:
With multiple enclosed regions:
Between curves containing parameters:
Generalizations and Extensions (3)
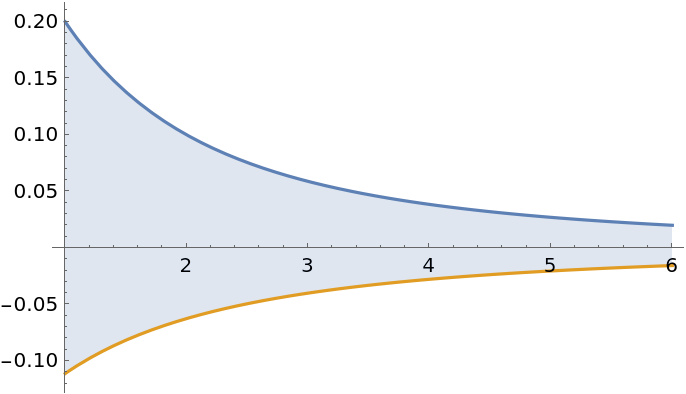
Find the area over an unbounded interval:
Curves with discontinuities over intervals:
With singularities:
Options (2)
Assumptions
The result may be conditioned on parameters:
Make an assumption about the parameter:
Applications (3)
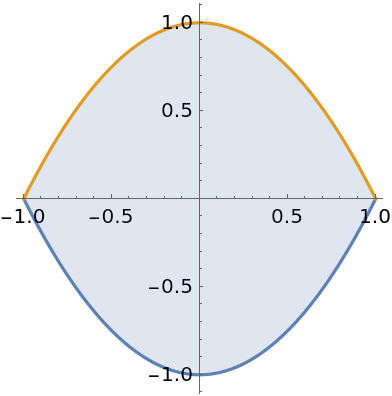
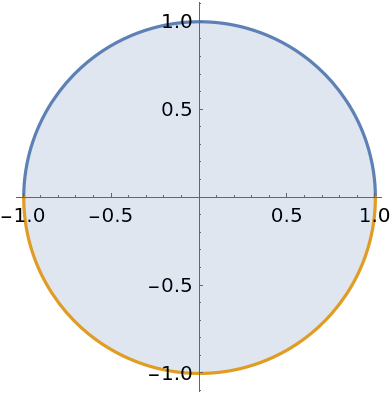
Compute the area of a disk:
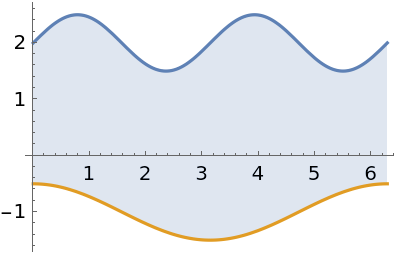
Cavalieri's principle states that the area between two curves does not change when each curve is shifted by the same amount:
The population of a region is currently growing at a rate of 35.208 ⅇ0.0083 t hundred people per year. It is thought that a large spike in employment opportunities can drop the growth rate to 24.098 ⅇ0.0071 t hundred people per year over the next five years. Find how many fewer people will be born if such a spike occurs:
Properties and Relations (5)
Area is always non-negative:
The order in which the curves are specified does not matter:
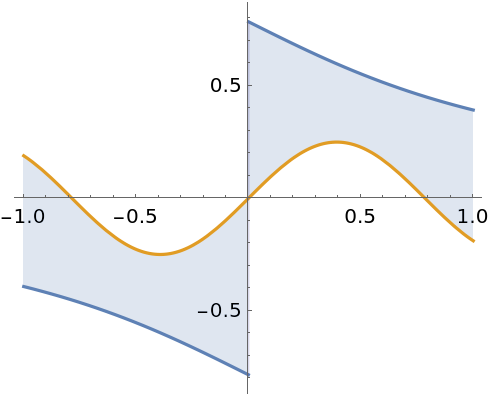
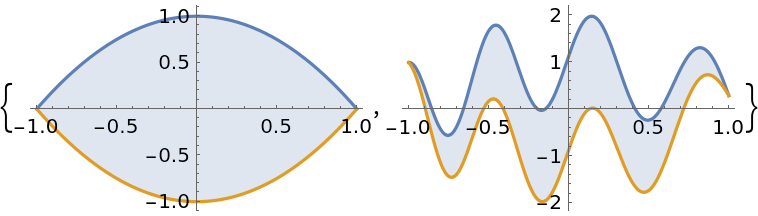
Find the area of multiple enclosed regions:
Sum over each enclosed region instead:
The area between two curves is the integral of the absolute value of their difference:
Possible Issues (2)
The integral defining the area between two curves may not converge:
In such cases, AreaBetweenCurves throws a message:
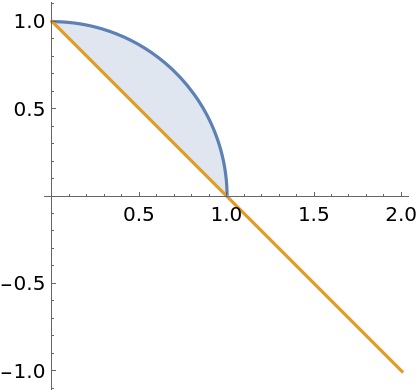
Functions must be real-valued over the entire range of integration. Here  is imaginary for x>1:
is imaginary for x>1:
AreaBetweenCurves throws a message to warn the user:
Restricting the domain of integration yields a result:

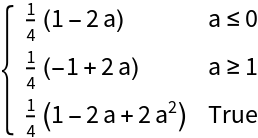
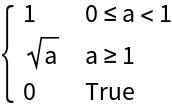
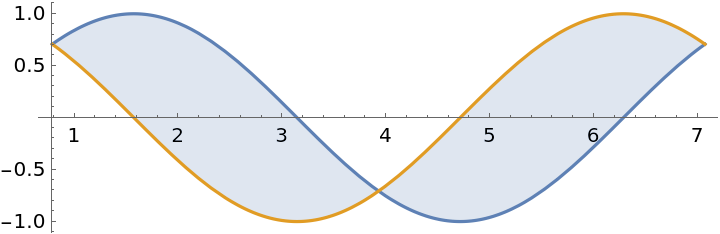
![ResourceFunction[
"AreaBetweenCurves"][{Sin[x], Cos[x]}, {x, \[Pi]/4, 3 \[Pi]/4}] + ResourceFunction[
"AreaBetweenCurves"][{Sin[x], Cos[x]}, {x, 3 \[Pi]/4, 5 \[Pi]/4}]](https://www.wolframcloud.com/obj/resourcesystem/images/abc/abc37cb4-4b69-4bcd-94ba-ec92af70b0da/5-3-1/518b8ac1bddde705.png)
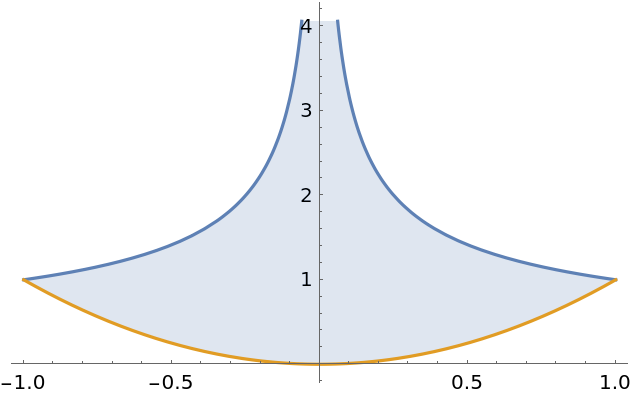
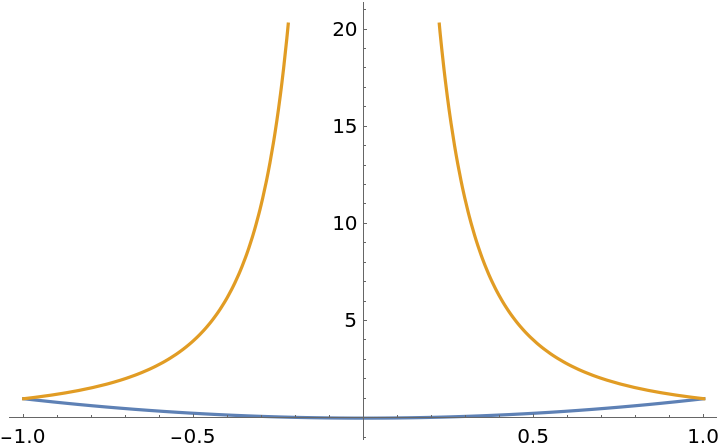
![funcs = {x^2, 1/x^2};
range = {x, -1, 1};
Plot[funcs, range]](https://www.wolframcloud.com/obj/resourcesystem/images/abc/abc37cb4-4b69-4bcd-94ba-ec92af70b0da/5-3-1/688e37cad90bfe1c.png)
![]() is imaginary for x>1:
is imaginary for x>1:![funcs = {Sqrt[1 - x^2], 1 - x};
range = {x, 0, 2};
Plot[funcs, range, AspectRatio -> Automatic, Filling -> {1 -> {2}}]](https://www.wolframcloud.com/obj/resourcesystem/images/abc/abc37cb4-4b69-4bcd-94ba-ec92af70b0da/5-3-1/768709a20624d225.png)